Hans Walser, [20181206]
Kreispackung
1 Worum geht es?
Eine Kreispackung im Rechteck fźhrt zum Goldenen Schnitt.
2 Die Packung
Einem Rechteck werden fźnf Kreise einbeschrieben gemŠ§ Abbildung 1.
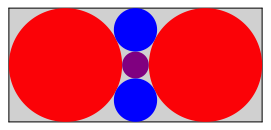
Abb. 1: Das Rechteck und die fźnf Kreise
Wie ist das SeitenverhŠltnis des Rechteckes? Wie gro§ sind die Kreise?
3 Bearbeitung
Wir verwenden die Ma§e und Bezeichnungen der Abbildung 2.
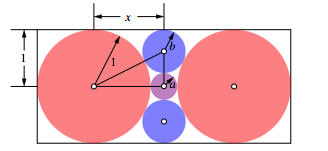
Abb. 2: Ma§e und Bezeichnungen
Die roten Kreise haben den Radius 1, der kleine lila Kreis den Radius a und die beiden blauen Kreise den Radius b. Der Abstand zwischen den Mittelpunkten eines roten Kreises und dem lila Kreis wird mit x bezeichnet.
Wir erhalten fźr a, b, x das quadratische Gleichungssystem:
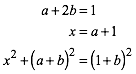 (1)
(1)
Das Gleichungssystem (1) hat folgende positive Lšsungen:
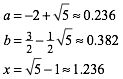 (2)
(2)
Das schmeckt gewaltig nach dem Goldenen Schnitt (Walser 2013). Mit
![]() (3)
(3)
ist:
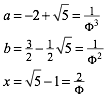 (4)
(4)
4 Das Goldene Rechteck
Das Goldene Rechteck (Rechteck mit dem SeitenverhŠltnis des Goldenen Schnittes) lŠsst sich an mehreren Orten in die Figur einpassen (Abb. 3, 4 und 5).

Abb. 3: Goldenes Rechteck
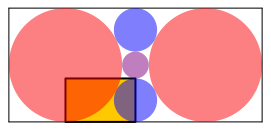
Abb. 4: Goldenes Rechteck
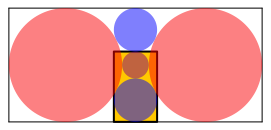
Abb. 5: Goldenes Rechteck
Umgekehrt kšnnen einem Goldenen Rechteck vier Halbkreise eingepasst werden (Abb. 6).
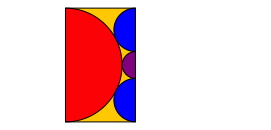
Abb. 6: Halbkreise im Goldenen Rechteck
Die drei kleinen Halbkreise passen zum Pentagramm (Abb. 7).
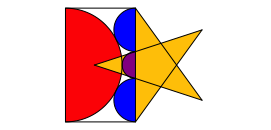
Abb. 7: Pentagramm
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.