Hans Walser, [20170423]
Kreisschar
1 Worum geht es?
Es wird eine Schar von konzentrischen Kreisen gezeigt, welche sowohl in regelm§igen Vielecken wie auch in der blichen Kugelparametrisierung erscheint.
2 Vielecke
2.1 Diagonalen
Die Abbildung 1 zeigt ein regelm§iges 36-Eck mit smtlichen Diagonalen.

Abb. 1: 36-Eck mit Diagonalen
Wir ãsehenÒ Kreise. Wie viele Kreise sind es? Welches sind ihre Radien?
ber Diagonalenschnittpunkt in regelm§igen Vielecken siehe [2] .
2.2 Diagonalen und Kreise
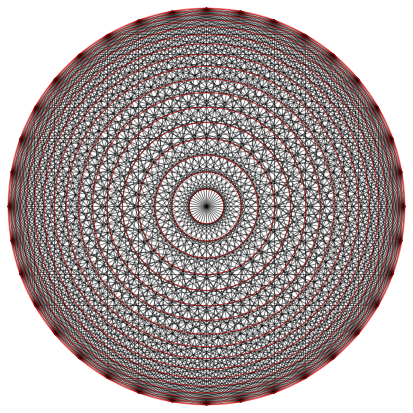
Abb. 2: Rote Kreise
In der Abbildung 2 sind die Kreise tatschlich rot eingezeichnet.
2.3 Nur Kreise

Abb. 3: Kreise
Die Abbildung 3 enthlt nur die roten Kreise.
Sehen wir da eine rumliche Figur?
3 Kugel
3.1 Parameterdarstellung
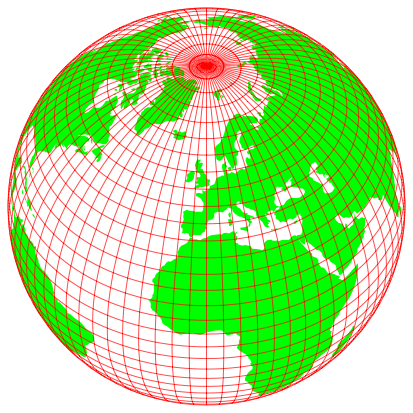
Abb. 4: Kugel
Die Kugel der Abbildung 4 ist mit der Maschenweite 5¡ parametrisiert. Geodaten aus Kartenprojektionen [1].
3.2 Blick auf den Nordpol
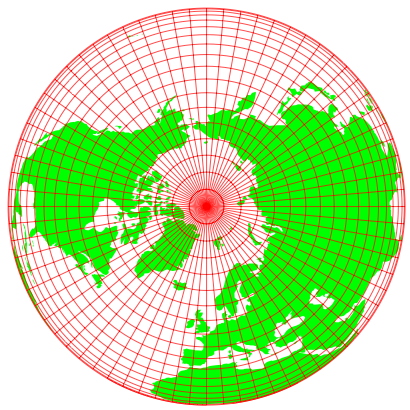
Abb. 5: Blick auf den Nordpol
Die Abbildung 5 zeigt dasselbe mit Blick auf den Nordpol.
Wir erkennen dieselben Kreise wie in den Abbildungen 1 bis 3.
4 Hintergrund
4.1 Regelm§ige Vielecke
4.1.1 Gerade Eckenzahl
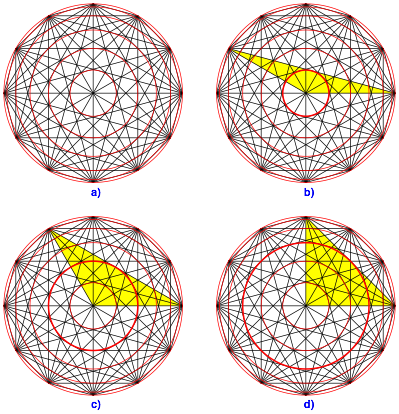
Abb. 6: Berechnung der Radien
Wir arbeiten exemplarisch im regelm§igen Zwlfeck (Abb. 6a). Die Mittelpunktdiagonalen schneiden sich unter Winkeln von 30¡. Zwei benachbarte Diagonalen welche vom selben Eckpunkt ausgehen schlie§en einen Winkel von 15¡ ein (Fcherwinkel). Den Umkreisradius setzen wir 1.
Der Radius r1 des innersten roten Kreises ist die Basishhe des in der Abbildung 6b gelb eingezeichneten gleichschenkligen Dreiecks. Dieses hat die Schenkellnge 1 und die Basiswinkel 15¡. Somit erhalten wir:
![]() (1)
(1)
Fr den Radius r2 des zweitinnersten Kreises arbeiten wir analog mit dem in der Abbildung 6c eingezeichneten Dreieck:
![]() (2)
(2)
Fr den Radius r3 ergibt sich (Abb. 6d):
![]() (3)
(3)
Wir sehen die allgemeine Gesetzm§igkeit:
![]() (4)
(4)
Die Abbildung 7 zeigt das Spektrum der Radien unter der Sinuskurve.
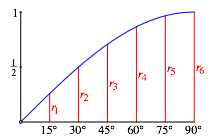
Abb. 7: Spektrum
Die Formel (4) lsst sich fr ein Vieleck gerader Eckenzahl n verallgemeinern zu:
![]() (5)
(5)
4.1.2 Ungerade Eckenzahl
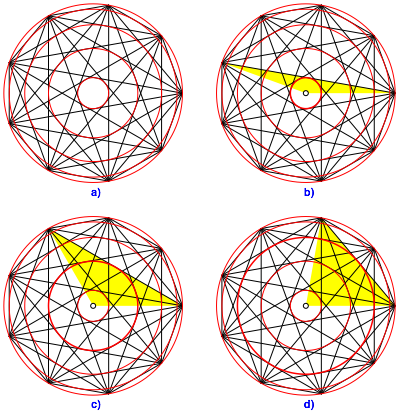
Abb. 8: Regelm§iges Neuneck
Wir arbeiten exemplarisch im regelm§igen Neuneck (Abb. 8a). Wir haben keine Mittelpunktdiagonalen, sondern ein ãLochÒ in der Mitte. Die gelben gleichschenkligen Dreiecke haben der Reihe nach die Basiswinkel 10¡, 30¡, 50¡. Wir haben eine ãversetzteÒ arithmetische Folge mit dem Versatz 10¡.
Fr die Radien der Kreise erhalten wir:
![]() (6)
(6)
Wir erkennen die Formel:
![]() (7)
(7)
Allgemein gilt fr ein Vieleck ungerader Eckenzahl n:
![]() (8)
(8)
Die Formeln (5) und (8) lassen sich zusammenfassen zu:
![]() (9)
(9)
4.2 Kugelparametrisierung
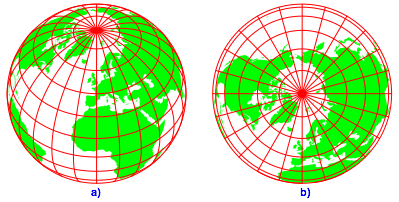
Abb. 9: Kugelparametrisierung
Die Kugelparametrisierung der Abbildung 9 arbeitet mit einem 15¡-Raster. Ein Meridian wird also durch die Breitenkreise in 12 Teile unterteilt.
Den Kugelradius setzen wir 1.
Wir berechnen nun die Radien der Breitenkreise (Abb. 9b).
Der erste Breitenkreis nach dem Nordpol gehrt zur geografischen Breite 75¡N. Seine Poldistanz ist daher 15¡. Die Poldistanz ist der Winkelabstand des Breitenkreises vom Nordpol. Poldistanz und geografische Breite ergnzen sich auf 90¡.
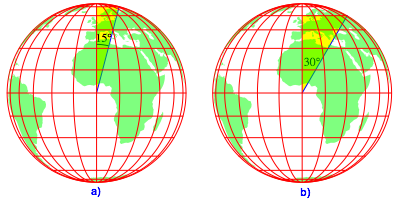
Abb. 10: Breitenkreisradien
Gem§ der Abbildung 10a erhalten wir fr den Radius r1 des ersten Breitenkreises nach dem Nordpol:
![]() (10)
(10)
Analog erhalten wir fr den zweiten Breitenkreis nach dem Nordpol (Abb. 10b) den Radius:
![]() (11)
(11)
Allgemein ist:
![]() (12)
(12)
Die Formel (12) ist identisch mit der Formel (4). Die Abbildung 11 zeigt die berlagerung der Abbildungen 6a (Diagonalen im Zwlfeck) und 9b (Blick auf den Nordpol). Es wird genau jeder zweite Meridian durch eine Diagonale des Zwlfecks abgedeckt.
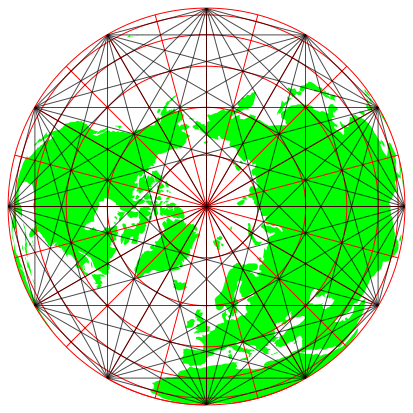
Abb. 11: berlagerung
Die Abbildung 12 zeigt eine grafische Variante.
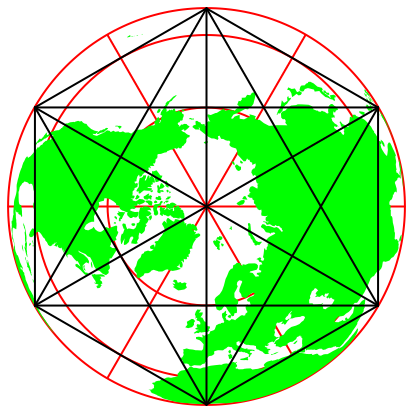
Abb. 12: Variante
Der Fall ãungeradeÒ kommt in der Kugelparametrisierung nicht vor. Warum nicht?
Websites
[1] ETH Zrich. Institut fr Kartografie und Geoinformation. Kartenprojektionen (24.04.2017):
http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html
[2] Hans Walser: Digonalenschnittpunkte in regelm§igen Vielecken (24.04.2017):
http://www.walser-h-m.ch/hans/Miniaturen/D/Diagonalenschnittpunkte/Diagonalenschnittpunkte.htm