Hans Walser, [20141010]
Kreisspiegelung
1 Worum geht es?
Es werden zwei verschiedene Konzepte zur Kreisspiegelung untersucht.
2 Die klassische Kreisspiegelung
2.1 Das Raster
Wir arbeiten mit dem Raster der Abbildung 1.
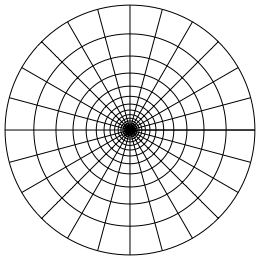
Abb. 1: Arbeitsraster
Dieser Raster entsteht in GeoGebra durch folgende Eingabezeilen:
Folge[Kurve[exp(a)*cos(b), exp(a)*sin(b), a, -¹, ¹], b, 0, 2*¹, ¹/12]
Folge[Kurve[exp(a)*cos(b), exp(a)*sin(b), b, -¹, ¹], a, -¹, ¹, ¹/12]
Die erste Eingabezeile gibt die radialen Geraden, die zweite Eingabezeile die Kreise mit exponentiell wachsenden Radien.
Die Karos des Rasters sind annhernd Quadrate.
2.2 Spieglung eines Punktes
Nun whlen wir einen der Kreise als Spiegelkreis (in der Abbildung 2 blau) und spiegeln einen Punkt durch Abzhlen der Karos. Dabei spielt es keine Rolle, ob wir von innen nach au§en spiegeln oder umgekehrt. Die Grundregel des Spiegelns ãgleich weit auf die andere SeiteÒ bezieht sich auf die Anzahl der Karos.
Da der Karoraster gegen das Zentrum des Spiegelkreises ãins UnendlicheÒ geht kann dieses Spiegelkreiszentrum nicht abgebildet werden. Man behilft sich, indem man einen ãunendlich fernen PunktÒ als Spiegelbild des Spiegelkreiszentrums postuliert.
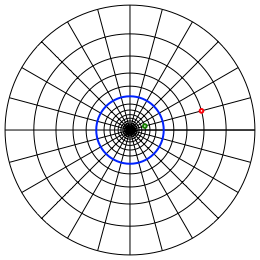
Abb. 2: Spiegelung eines Punktes
Die Abbildung 3 zeigt, wie das konstruktiv mit Zirkel und Lineal oder mit dynamischer Geometrie-Software gemacht werden kann. Dazu bentigen wir lediglich den Spiegelkreis und seinen Mittelpunkt. Das Arbeitsraster bentigen wir nicht mehr.

Abb. 3: Konstruktives Vorgehen
2.3 Bild des Smiley
In der Abbildung 4 ist das grne Gesicht von innen nach au§en gespiegelt worden. Wir stellen fest: Die Kreisspiegelung ist kreistreu insofern als ein Kreis als Gesamtes auf einen Kreis abgebildet wird. Allerdings gibt es Binnenverzerrungen, und daher ist die Bildfigur verzerrt. Das grne Gesicht ist bis auf die Locke symmetrisch, das rote nicht. Wir haben emotional Probleme, von einer ãSpiegelungÒ zu reden.
Die Locke hat sich gewendet. Wir haben eine Orientierungsnderung.

Abb. 4: Bild des Smiley
In der Abbildung 5 ist das grne Gesicht von au§en nach innen gespiegelt worden.

Abb. 5: Von au§en nach innen
In der Abbildung 6 ist das grne Gesicht so verzerrt gezeichnet, dass die Verzerrung im Prinzip erhalten bleibt. Die Situation deckt sich mit unserer Vorstellung von ãSpiegelungÒ.
Abgesehen von der Locke ist es eine zentrische Streckung, also eine hnlichkeitsabbildung.

Abb. 6: Verzerrungstreue Abbildung
Um das zu erhalten, wurde mit ãAbzhlen der KarosÒ gearbeitet (Abb. 7). Das grne Gesicht wurde bereits im Karoraster gezeichnet.

Abb. 7: Abzhlen der Karos
3 Neuer Raster
3.1 Das Raster
Wir arbeiten nun mit dem Raster der Abbildung 8.
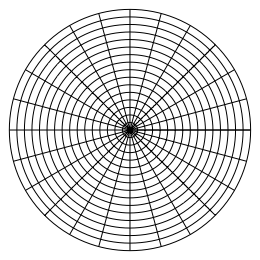
Abb. 8: Neues Raster
Die Radien der Kreise wachsen gleichm§ig. Die Karos des Rasters sind nun aber nicht mehr angenhert Quadrate.
Das Raster entsteht in GeoGebra durch folgende Eingabezeilen:
Folge[Kurve[a*cos(b), a*sin(b), a, 0, 2], b, 0, 2*¹, ¹/12]
Folge[Kurve[a*cos(b), a*sin(b), b, –¹, ¹], a, 0, 2, 1/8]
Die erste Eingabezeile gibt die radialen Geraden, die zweite Eingabezeile die Kreise mit gleichm§ig zunehmenden Radien.
3.2 Spiegelung eines Punktes
Nun whlen wir wieder einen Spiegelkreis (blau) und versuchen einen Punkt im Innern nach au§en zu spiegeln indem wir ãgleich weitÒ auf die andere Seite der Kreislinie gehen. Wir stellen fest, dass es zwei Mglichkeiten gibt (Abb. 9). Wir haben es also nicht mehr mit einer eindeutigen Abbildung im Sinne der Mathematik zu tun. Wehe wenn das der Lehrer sieht!
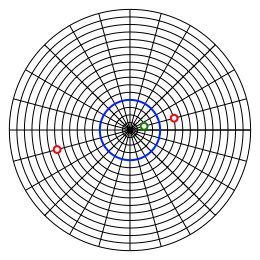
Abb. 9: Wie kommen wir nach au§en?
Man kann da jetzt ein bisschen philosophieren. In der Schule lernen wir, dass wir auf dem krzesten Weg ber die Stra§e gehen sollen. Wenn wir entsprechend auf dem krzesten Weg ber den blauen Spiegelkreis gehen wollen, ist der rote Punkt rechts der ãrichtigeÒ. Damit ist die Abbildung von innen nach au§en eindeutig definiert.
Mit einer Ausnahme. Fr das Zentrum des Spiegelkreises kommen alle Punkte auf einem Kreis mit dem doppelten Radius des Spiegelkreises als Bildpunkte in Frage. Das hei§t umgekehrt, dass die Punkte auf diesem doppelt so gro§en Kreis auf das Spiegelkreiszentrum abgebildet werden knnen.
Der rote Punkt links gehrt zur Bummelvariante ãauf dem lngsten WegÒ.
Die Abbildung 10 zeigt ein Beispiel mit einem Startpunkt au§erhalb des Kreises. Ein Bildpunkt ist im Innern des Kreises. Ein weiterer Bildpunkt ist au§erhalb.
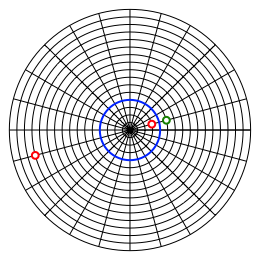
Abb. 10: Startpunkt au§erhalb
Wenn der Startpunkt mehr als der Durchmesser des blauen Spiegelkreises von diesem entfernt ist, sind sogar beide Bildpunkt au§erhalb.
Die Konstruktion des Spiegelpunktes kann natrlich auch ohne Raster durchgefhrt werden (Abb. 11).
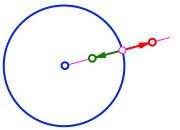
Abb. 11: Konstruktion ohne Raster
3.3 Bild des Smiley
Im Folgenden einige Bilder des Smiley.
Die Abbildung 13 zeigt eine Spiegelung von innen nach au§en. Die Bilder der Kreise sehen aus wie Ellipsen, sind aber keine. Dies wird durch die Abbildung 13 illustriert. Die Bilder der Kreise sind eher bananenfrmig.
Die rote Locke ist spiegelbildlich zur grnen Locke.

Abb. 12: Von innen nach au§en

Abb. 13: Das Bild ist keine Ellipse
Die Abbildung 14 zeigt den Weg von au§en nach innen. Die Bilder der Kreise werden eifrmig, mit der ãSpitzeÒ gegen den Mittelpunkt des Spiegelkreises.
Die rote Locke ist spiegelbildlich zur grnen Locke.
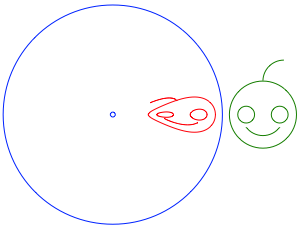
Abb. 14: Von au§en nach innen
Im Beispiel der Abbildung 15 berstreicht der grne Urbildkreis den Kreis mit dem doppelten Radius des Spiegelkreises. Es werden daher mehrere Punkte ins Zentrum des Spiegelkreises abgebildet. Der Umrisskreis des grnen Kopfes wird zu einer liegenden Acht.
ber die rote Locke kann man sich Gedanken machen.
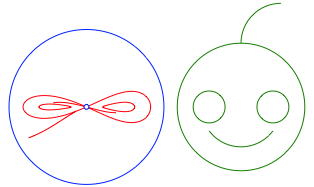
Abb. 15: Was ist hier los?
In der Abbildung 16 wird kopfber die Flucht nach links angetreten.
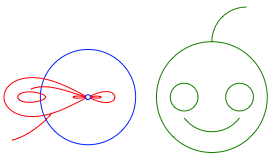
Abb. 16: Flucht nach links
Im Beispiel der Abbildung 17 bleibt die Orientierung erhalten.
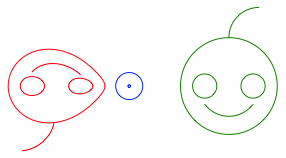
Abb. 17: Orientierungserhaltend
Wenn der Spiegelkreis relativ zum Urbild zu einem Punkt zusammenschrumpft, ergibt sich eine Punktspiegelung (Abb. 18).
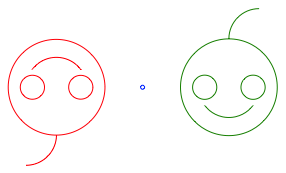
Abb. 18: Der Spiegelkreis schrumpft zu einem Punkt