1 Worum geht es?

Variante zu einem Konstruktionsvorgang bei der Kreisspiegelung.

2 Normierung

Wir wählen ein allfälliges Koordinatensystem jeweils so, dass der Spiegelkreis k der Einheitskreis ist und der zu spiegelnde Punkt P auf der positiven x-Achse.

3 Von innen nach außen

Ein Urbildpunkt P im Innern des Spiegelkreises k soll nach außen gespiegelt werden.

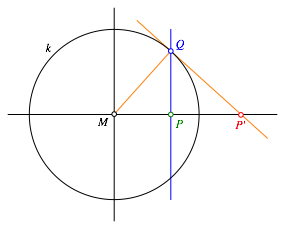
Abb. 1: Konstruktion des Spiegelpunktes

Die Abbildung 1 zeigt ein mögliches Konstruktionsverfahren. Die Senkrechte durch den Urbildpunkt P wird mit dem Spiegelkreis k geschnitten. Im Schnittpunkt Q zeichnen wir die Tangente an den Spiegelkreis k und schneiden diese mit der Geraden MP (also mit der x-Achse). Der Schnittpunkt ist der gesuchte Bildpunkt P’.

4 Konstruktionseinschränkung

Das Verfahren funktioniert nur, wenn sich der Urbildpunkt P im Innern des Spiegelkreises k befindet. Es gibt Konstruktionsverfahren, welche keine solche Einschränkung kennen (Abb. 2).

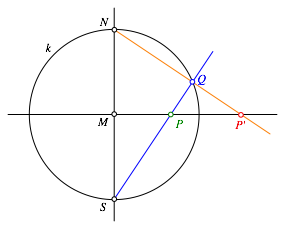
Abb. 2: Anderes Verfahren

5 Mittelsenkrechte

Wir modifizieren das Verfahren der Abbildung 1, indem wir mit Mittelsenkrechten arbeiten (Abb. 3).

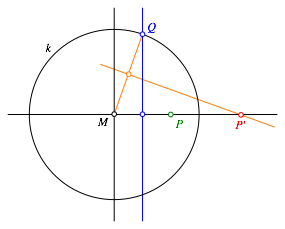
Abb. 3: Verfahren mit Mittelsenkrechten

Wir schneiden die Mittelsenkrechte von MP mit dem Spiegelkreis k. Dies ergibt den Schnittpunkt Q. Nun schneiden wir die Mittelsenkrechte von MQ mit der Geraden MP und erhalten so den Bildpunkt P’. Beweis folgt.

Dieses Verfahren hat eine größere Reichweite. Der Urbildpunkt P kann jetzt auch außerhalb des Spiegelkreises liegen, allerdings nur innerhalb des Kreises mit dem doppelten Radius des Spiegelkreises.

6 Drittelsenkrechte

Oh je, oh je, der Begriff Drittelsenkrechte fehlt im Kanon von Lehrer Lämpel. Zudem gibt es zwei Versionen (Abb. 4 und 5). Da ist Sprachkompetenz angesagt.

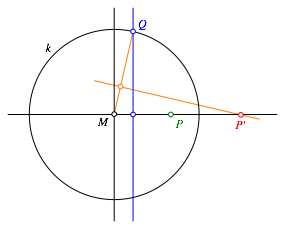
Abb. 4: Die eine Drittelsenkrechte

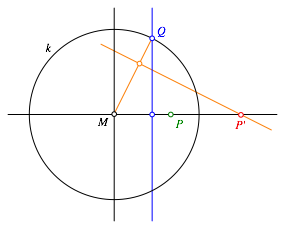
Abb. 5: Die andere Drittelsenkrechte

Wie steht es mit den Reichweiten dieser Konstruktionen?

7 Allgemeiner Fall. Beweis

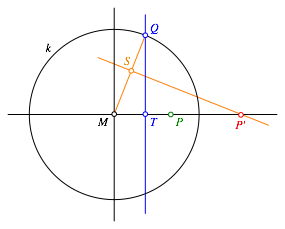
Abb. 6: Allgemeiner Fall

Wir strecken den Urbildpunkt P vom Kreismittelpunkt M aus mit dem Faktor t. In der Abbildung 6 wurde exemplarisch t = 0.55 gewählt. Der Faktor t kann aber auch größer als 1 oder negativ gewählt werden. Durch diese Streckung erhalten wir den Punkt T. Die Senkrechte durch T schneiden wir mit dem Spiegelkreis k in Q. Nun strecken wir Q von M aus mit demselben Faktor t und zeichnen im Bildpunkt S die Senkrechte zu MQ. Diese schneiden wir mit der Geraden MP und erhalten so P’.

Wir müssen nun zeigen, dass P’ der Spiegelpunkt von P bei der Kreisspiegelung an k ist. Dazu zeichnen wir noch die Tangente in Q an k ein und schneiden diese mit MP in T’. Gemäß dem Verfahren der Abbildung 1 ist T’ der Bildpunkt von T bei der Kreisspiegelung an k.

Die Geraden SP’ und QT’ sind beide senkrecht zu MQ und daher untereinander parallel. Wir können also die Strahlensätze anwenden.

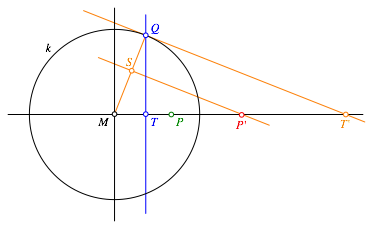
Abb. 7: Beweisfigur

Der Beweis geht nun rechnerisch. Wir setzen . Wegen der Streckung ist . Wegen der Kreisspiegelung ist . Und wegen dem Strahlensatz schließlich . Damit ist P’ tatsächlich das Spiegelbild von P bei der Kreisspiegelung an k.

Abb. 8: Viertelsenkrechte

Literatur

Borges, Florian 2019: Großes Sparpotenzial in der Mathematik wiederentdeckt: Geometrie mit dem Zirkel und ohne Lineal. MNU Journal – Ausgabe 04.2019 – ISSN 0025-5866.