Hans Walser, [20190810]
Kreisspiegelung
Anregung: Borges 2019
1 Worum geht es?
Rechnerische Lsung fr eine Kreisspiegelung nur mit dem Zirkel.
2 Kreisspiegelung nur mit dem Zirkel
Borges 2019 beschreibt einen Konstruktionsvorgang der Kreisspiegelung nur mit dem Zirkel. Er geht wie folgt (Abb. 1).
Es sei e der Inversionskreis, O dessen Mittelunkt und P der zu spiegelnde Urbildpunkt.
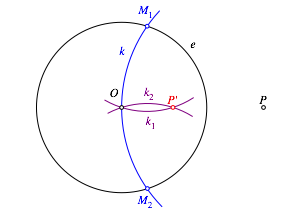
Abb. 1: Konstruktionsvorgang mit dem Zirkel allein
Wir
schneiden den Kreis k um P durch O mit dem Inversionskreis e
und erhalten die beiden Schnittpunkte ![]() und
und ![]() .
.
Weiter
zeichnen wir die Kreise ![]() und
und ![]() um
um ![]() beziehungsweise
beziehungsweise ![]() durch O.
durch O.
Der zweite Schnittpunkt dieser beiden Kreise ist der gesuchte Bildpunkt PÕ.
Die Stimmigkeit dieser Konstruktion ergibt sich aus dem Nachfolgenden.
3 Diskussion
Wenn der Abstand des Urbildpunkte P von O kleiner ist als der halbe Radius des Inversionskreises e, schneiden sich e und k nicht.
Man kann die Sache retten, indem man den Urbildpunkt um ein geeignetes ganzzahliges Vielfaches seines Abstandes von O entfernt (Hilfspunkt Q), den Hilfspunkt Q spiegelt und den Spiegelpunkt QÕ um dasselbe ganzzahlige Vielfache von O entfernt. Die ganzzahligen Vielfachen knnen mit einem Raster aus gleichseitigen Dreiecken mit dem Zirkel allein konstruiert werden.
Dieses Konstruktionsverfahren mit der Hilfskonstruktion ist nicht Zugmodus-resistent. Wir wissen ja zum vorneherein nicht welches Vielfache bentigt wird. Es gibt daher keine Konstruktionsbeschreibung fr dieses Verfahren mit einer festen Anzahl Konstruktionsschritten.
Randbemerkung: Wenn Zirkel und Lineal zugelassen sind, gibt es mehrere Zugmodus-resistente Verfahren ohne Fallunterscheidung hinsichtlich der Lage von P.
4 Rechnerische Lsung
Wir arbeiten statt auf dem Papier im Modell der Koordinatengeometrie. Da wir nur den Zirkel bentzen drfen, hei§t das, dass wir nur die Kreisgleichung verwenden drfen. In diesem Modell arbeiten wir nach dem oben geschilderten Verfahren.
Gegeben
sei also der Inversionskreis e und
der Urbildpunkt P. Wir whlen das
Koordinatensystem so, dass der Inversionskreis e der Einheitskreis ist und der Urbildpunkt P die Koordinaten ![]() ,
hat.
,
hat.
Und jetzt frisch drauflos.
Inversionskreis e:
![]() (1)
(1)
Kreis k:
![]() (2)
(2)
Das durch (1) und (2) gegebene quadratische Gleichungssystem hat, wie man durch Einsetzen sofort verifiziert, die Lsungen:
![]() (3)
(3)
Kreise ![]() und
und ![]() :
:
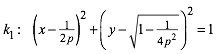 (4)
(4)
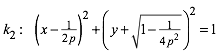 (5)
(5)
Das durch (4) und (5) gegebene quadratische Gleichungssystem hat die beiden Lsungen:
![]() (6)
(6)
Voil. Damit ist auch die Stimmigkeit der oben im Papiermodell durchgefhrten Konstruktion bewiesen.
5 Nochmals Diskussion
In (3)
erhalten wir fr ![]() rein
imaginre y-Koordinaten der beiden
Lsungen. Entsprechend sind auch die Kreise
rein
imaginre y-Koordinaten der beiden
Lsungen. Entsprechend sind auch die Kreise ![]() und
und ![]() nicht
reell sichtbar. Ihre beiden Schnittpunkte sind aber reell. Nach dem finsteren
Korridor kommen wir wieder ans reelle Licht.
nicht
reell sichtbar. Ihre beiden Schnittpunkte sind aber reell. Nach dem finsteren
Korridor kommen wir wieder ans reelle Licht.
Das Verfahren ist also unabhngig von der Gr§e von p und damit Zugmodus-resistent.
Literatur
Borges, Florian 2019: Gro§es Sparpotenzial in der Mathematik wiederentdeckt: Geometrie mit dem Zirkel und ohne Lineal. MNU Journal – Ausgabe 04.2019 – ISSN 0025-5866.
Website
Hans Walser: Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kreisspiegelung2/Kreisspiegelung2.htm