Hans Walser, [20190812]
Kreisspiegelung
Anregung: Borges 2019
1 Worum geht es?
Beispiele von Zugmodus-resistenten Konstruktionen der Kreisspiegelung.
2 Kreisspiegelung
Bei einer Kreisspiegelung oder Kreisinversion eines Punktes P an einem Kreis mit Mittelpunkt O und Radius r (Abb. 1) gilt:
![]() (1)
(1)
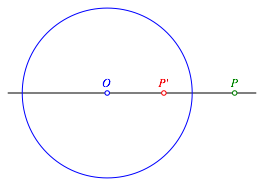
Abb. 1: Kreisspiegelung
Fr die
folgenden berlegungen normieren wir bei Bedarf wie folgt: r = 1, O sei der Ursprung
eines kartesischen Koordinatensystems (der Inversionskreis ist also der Einheitskreis),
der Urbildpunkt P liegt auf der
positiven x-Achse. In diesem
Koordinatensystem haben wir ![]() und
und ![]() . Aus (1) wird:
. Aus (1) wird:
![]() (2)
(2)
Bei den folgenden Konstruktionen mssen wir jeweils (2) nachweisen.
Lehrer Lmpel: Die Formeln (1) und (2) sind symmetrisch bezglich Urbildpunkt und Bildpunkt. Die Kreisspiegelung geht hin und zurck nach demselben Muster.
3 Klassische Konstruktionen
Die in der Schule tradierten klassischen Konstruktionen unterscheiden je nachdem, ob von au§en nach innen oder von innen nach au§en gespiegelt wird.
3.1 Von au§en nach innen
Tangenten von P an den Inversionskreis. Gerade durch die Berhrungspunkte mit der Geraden OP schneiden, gibt Bildpunkt PÕ (Abb. 2).
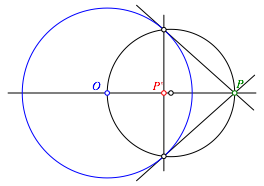
Abb. 2: Von au§en nach innen
Die Stimmigkeit der Konstruktion ergibt sich mit dem Kathetensatz im in der Abbildung 3 gelb eingezeichneten rechtwinkligen Dreieck (richtig: der Kathetensatz, einer der Stze, wo Sie sich gefragt haben, wozu sie gut sind).
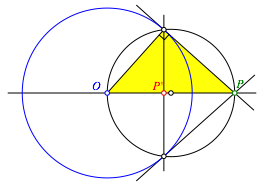
Abb. 3: Beweis mit Kathetensatz
Lehrer Lmpel: Asymmetrische Behandlung von P und PÕ. Ganze Hypotenuse zu Hypotenusenabschnitt.
3.2 Von innen nach au§en
Lot in P auf die Gerade OP mit Inversionskreis schneiden. Tangenten in diesen Punkten. Schnittpunkt der Tangenten ist PÕ (Abb. 4).
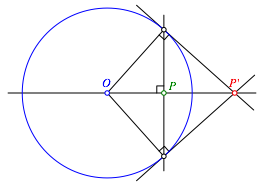
Abb. 4: Von innen nach au§en
Nachweis ebenfalls mit Kathetensatz wie bei Abbildung 3.
4 Diskussion
Die beiden oben beschriebenen Konstruktionsverfahren sind nicht Zugmodus-resistent.
Gesucht sind Verfahren, die unabhngig von der Lage des Urbildpunktes P funktionieren. Im Folgenden einige Beispiele solcher Verfahren. Ich habe sie experimentell geprft.
5 Stereografische Projektion
Man soll sich durch den hochgestochenen Titel nicht irritieren lassen. Die Sache ist ganz einfach und die Konstruktion elegant (Abb. 5).
Die Punkte N und S sind die Schnittpunkte des Lotes in O auf OP mit dem Inversionskreis. Wir schneiden die Gerade PN mit dem Inversionskreis. Die Verbindung von S mit diesem Punkt schneiden wir mit der Geraden OP. Der Schnittpunkt ist PÕ.
Dieses Verfahren funktioniert unabhngig von der Lage von P. Es ist also geeignet, um ein Makro fr die Kreisspiegelung zu bauen.
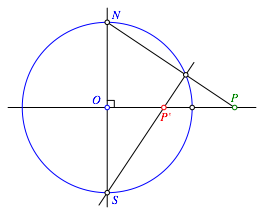
Abb. 5: Stereografische Projektion
Die Stimmigkeit dieser Konstruktion ergibt sich aus der hnlichkeit der beiden in der Abbildung 6 eingezeichneten rechtwinkligen Dreiecke.
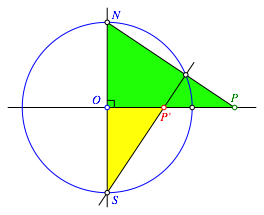
Abb. 6: Beweis mit hnlichen rechtwinkligen Dreiecken
Die Bezeichnung stereografische Projektion ist in der Kartografie gelufig. Wir denken uns den Inversionskreis ersetzt durch die Erdkugel und die Gerade OP durch die quatorebene. Die stereografische Projektion ist nun die Zentralprojektion von einem der beiden Pole aus auf die quatorebene. Die stereografische Projektion ist winkeltreu (conformal) und Mbiuskreis-treu. Unter Mbiuskreisen fasst man ãechteÒ Kreise und Geraden zusammen, indem man letztere als Kreis mit der Krmmung null interpretiert.
Die Kreisspiegelung kann also mit einem Trick ber den Raum gemacht werden. Wir projizieren die quatorebene vom Nordpol aus auf die Kugel und das Kugelbild vom Sdpol aus wieder auf die quatorebene. Das entspricht insgesamt einer Kreisspiegelung der quatorebene am quatorkreis.
6 Hhensatz
Das Lot in N auf die Gerade PN schneiden wir mit der Geraden OP. Den Schnittpunkt Q spiegeln wir an O und erhalten so PÕ (Abb. 7).
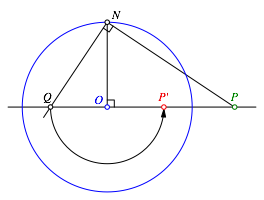
Abb. 7: Lot und Spiegeln
Die Stimmigkeit der Konstruktion ergibt sich aus dem Hhensatz im rechtwinkligen Dreieck (Abb. 8).
Den beiden gleichberechtigten Hypotenusenabschnitten entsprechen die Punkte P beziehungsweise PÕ. Der Lehrer Lmpel kann also zufrieden sein.
Das Verfahren funktioniert unabhngig von der Lage von P. Es ist also geeignet, um ein Makro fr die Kreisspiegelung zu bauen.
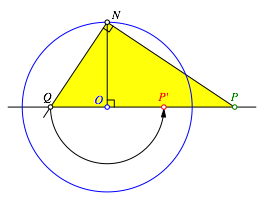
Abb. 8: Hhensatz
7 Gnomon
Das Verfahren ist etwas akademisch. Es ist einfach der geometrische Nachvollzug der Formeln (1) und (2).
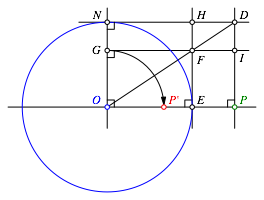
Abb. 9: Wie die alten Griechen rechneten
Wir zeichnen zunchst durch N eine Parallele zu OP (Abb. 9). Das Lot in P zu OP schneiden wir mit dieser Parallelen in D. Die Gerade OD schneiden wir mit dem Lot in E zu OP. Durch den Schnittpunkt F zeichnen wir eine Parallele zu OP und schneiden diese mit der Geraden ON. Den Kreis um O durch den Schnittpunkt G schneiden wir mit OP und erhalten so den Bildpunkt PÕ.
Das Verfahren funktioniert unabhngig von der Lage von P. Es ist also geeignet, um ein Makro fr die Kreisspiegelung zu bauen.
Die Stimmigkeit der Konstruktion ergibt sich aus der Flchengleichheit des Einheitsquadrates OEHN und des Rechteckes OPIG (Gnomon-Verfahren, Abb. 10).
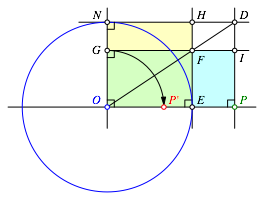
Abb. 10: Flchengleichheit
Literatur
Borges, Florian 2019: Gro§es Sparpotenzial in der Mathematik wiederentdeckt: Geometrie mit dem Zirkel und ohne Lineal. MNU Journal – Ausgabe 04.2019 – ISSN 0025-5866.
Websites
Hans Walser: Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kreisspiegelung2/Kreisspiegelung2.htm
Hans Walser: Kreisspiegelung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kreisspiegelung3/Kreisspiegelung3.htm