Hans Walser, [20181229]
Kreuz des Pythagoras
1 Worum geht es?
Eine Spielerei um die Pythagorasfigur.
2 Pythagorasfigur
Wir beginnen mit einem rechtwinkligen, aber sonst beliebigen Dreieck und ergŠnzen zur źblichen Pythagorasfigur (Abb. 1).
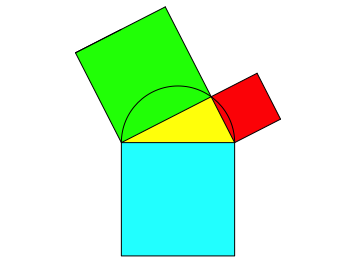
Abb. 1: Pythagorasfigur
3 †berhang
Es fŠllt auf (was mir bis jetzt allerdings noch nie aufgefallen ist), dass der †berhang links und rechts gleich gro§ ist, und zwar so gro§ wie die Dreieckshšhe (Abb. 2).
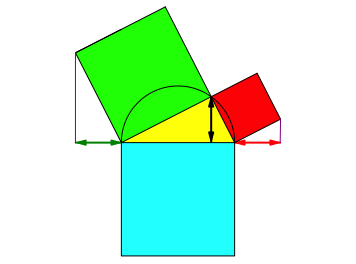
Abb. 2: Gleicher †berhang
Der Beweis ergibt sich durch Zerlegung des rechtwinkligen Dreiecks mittels der Hšhe (Abb. 3).
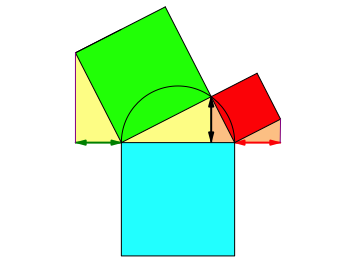
Abb. 3: Zerlegungsbeweis
4 Halbieren der Kathetenquadrate
Wir halbieren die beiden Kathetenquadrate mit einer Diagonalen und ordnen die oberen HŠlften in umgekehrter Reihenfolge an (Abb. 4).
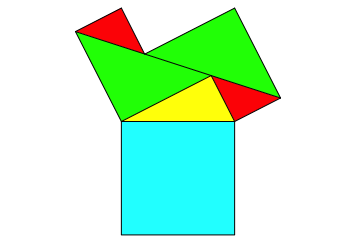
Abb. 4: Halbieren der Kathetenquadrate
5 ErgŠnzung zum Kreuz
Die beiden oberen Spitzen liegen nun genau gleich hoch und senkrecht źber der linken und rechten oberen Ecke des Hypotenusenquadrates. Wir kšnnen also eine Kopie des Hypotenusenquadrates hinaufschieben und aufsetzen (Abb. 5).
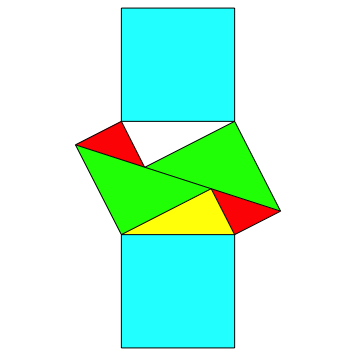
Abb. 5: Hinaufschieben des Hypotenusenquadrates
Weiter ist es so, dass der Abstand der beiden Hypotenusenquadrate genau die LŠnge der Hypotenuse ist. Wir kšnnen das sichtbar machen, indem wir links und rechts je ein weiteres Hypotenusenquadrat ansetzen (Abb. 6). So erhalten wir das Kreuz des Pythagoras.
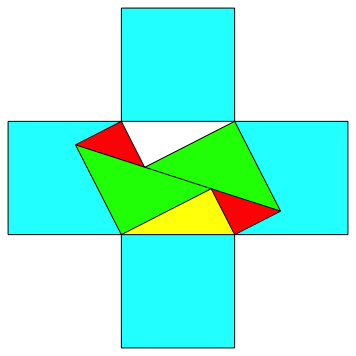
Abb. 6: Kreuz des Pythagoras
Der Beweis fźr die Stimmigkeit der Figur ergibt sich durch Einpassen des rechtwinkligen Dreieckes an verschiedenen Orten (Abb. 7).
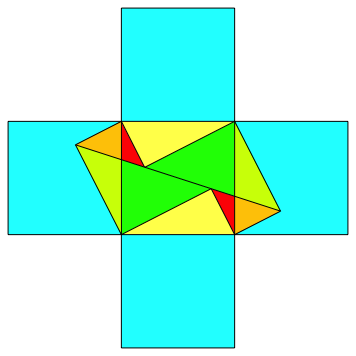
Abb. 7: Beweisfigur
6 Zerlegungsbeweis fźr den Satz von Pythagoras
Die Abbildung 7 motiviert einen mir bislang unbekannten (oder vergessenen) Zerlegungsbeweis fźr den Satz des Pythagoras (Abb. 8 und 9).
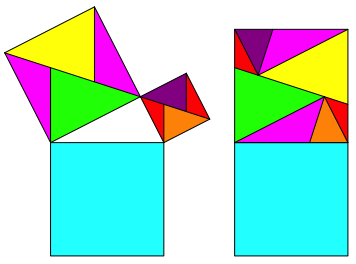
Abb. 8: Zerlegungsbeweis
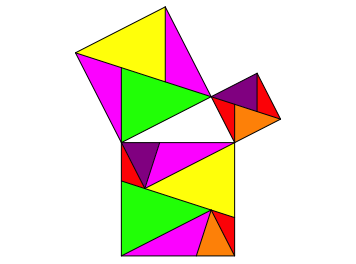
Abb. 9: Zerlegungsbeweis