Hans Walser, [20100207a]
Krmmung
1 Idee
In einem gekrmmten
Eisenbahngeleise ist die u§ere Schiene lnger als die innere. Diese Differenz
hngt natrlich von der Spurweite ab. Bei Breitspur ist sie gr§er als bei
Schmalspur. Diese Differenz hngt aber auch von der Geleiselnge ab. Bei einem
vollen Kreis ist sie doppelt so gro§ wie bei einem Halbkreis. Wir werden diese
Differenz als Ma§ fr die totale Krmmung verwenden.
2
Einheitsspur
2.1
Gleisbau
Quer zu einer Kurve
zeichnen wir in regelm§igen Abstnden Schwellen, auf denen wir nach links und
nach rechts je eine halbe Einheit abtragen. Darauf montieren wir die Schienen.
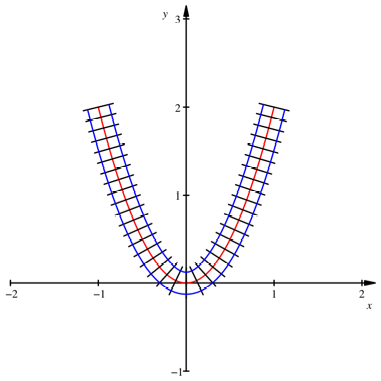
Die Abbildung zeigt das Vorgehen am Beispiel der Parabel:
![]()
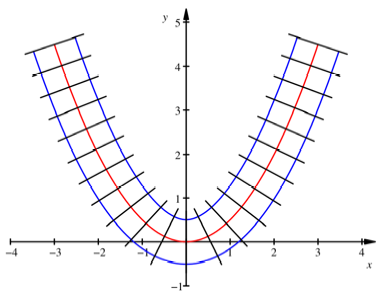
Parabel
2.2
Differenz der Gleislngen
Fr das obige Beispiel ![]() knnen numerisch
folgende Daten bestimmt werden:
knnen numerisch
folgende Daten bestimmt werden:
Trasselnge = 11.30527944
Spurweite = 1
Schienenlnge rechts = 12.55432521
Schienenlnge links = 10.05623367
Mittlere Schienenlnge = 11.30527944
Totale Krmmung = 2.498091545 = 143.1301024¡
Mittlere Krmmung = 0.220966811
Die Schienenlnge
rechts ist lnger, die Schienenlnge links krzer als die Trasselnge. Die
Trasselnge ist offenbar der Mittelwert der beiden Schienenlngen. Die
Differenz der beiden Schienenlngen wird hier offenbar als totale Krmmung
bezeichnet. Dafr besteht Erklrungsbedarf, ebenso fr die Angabe der totalen
Krmmung als Winkel und den Begriff der mittleren Krmmung.
3
Totale Krmmung
3.1
Definitionen
Unter der totalen
Krmmung einer Trasse mit Spurweite 1
verstehen wir die Differenz der Schienenlnge rechts minus der Schienenlnge
links. ãRechtsÒ und ãlinksÒ sind im Sinne des Kurvendurchlaufes zu verstehen.
Die Schienenlnge rechts kann durchaus die krzere sein, wir haben dann eine
negative totale Krmmung.
Wenn wir die totale
Krmmung als Winkel im Bogenma§ (oder umgerechnet ins Degree-Ma§) verstehen,
erhalten wir den Schnittwinkel zwischen den Trgergeraden der ersten und der
letzten Schwelle.
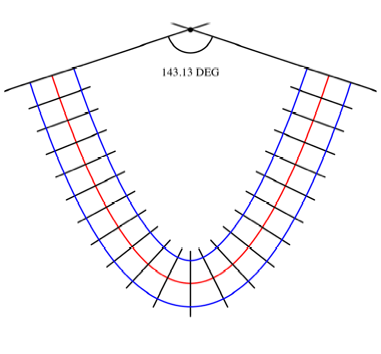
Winkel-nderung
Da die Schwellen
orthogonal zur Kurve sind, hei§t das aber auch, dass die totale Krmmung die Richtungsnderung der Kurve zwischen Startpunkt und Endpunkt angibt.
Die mittlere
Krmmung schlie§lich ist die totale
Krmmung dividiert durch die Trasselnge.
3.2
Tcken
3.2.1
Scharfe Kurven
Bei vorgegebener Spurweite
1 kriegen wir nicht jede Kurve. Bei der Parabel ![]() macht die innere
Schiene seltsame Kapriolen.
macht die innere
Schiene seltsame Kapriolen.
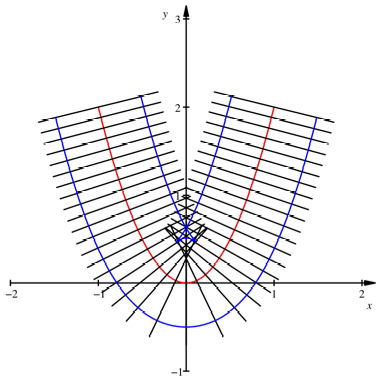
Probleme mit der inneren
Schiene
Auch die berechneten
Daten machen stutzig:
Trasselnge = 4.646783762
Spurweite = 1
Schienenlnge rechts = 5.972601426
Schienenlnge links = 3.792890953
Mittlere Schienenlnge = 4.88274619
Totale Krmmung = 2.179710473 = 124.8882107¡
Mittlere Krmmung = 0.4690793858
Die mittlere
Schienenlnge ist etwas gr§er als die Trasselnge. Das Problem ist, dass die
innere Schiene ein Stck weit rckwrts geht, aber das Computerprogramm diese
Strecke trotzdem additiv behandelt. Als Folge sind auch die totale und die
mittlere Krmmung falsch angegeben.
Wir knnen die Probleme
angehen, indem wir die Spurweite verkleinern. Dabei wird allerdings die
Differenz der Schienenlngen und entsprechend kleiner. Das knnen wir aber
kompensieren, indem wir diese Differenz durch die Spurweite dividieren. Somit
haben wir eine erweiterte Definition der totalen Krmmung:
Unter
der totalen Krmmung einer Trasse mit
beliebiger Spurweite verstehen wir die Differenz der Schienenlnge rechts minus
der Schienenlnge links, dividiert durch die Spurweite.
Wenn wir die Parabel ![]() mit der
Spurweite
mit der
Spurweite ![]() bearbeiten,
sieht das so aus:
bearbeiten,
sieht das so aus:
Trasselnge = 4.646783762
Spurweite = 1/2
Schienenlnge rechts = 5.309692594
Schienenlnge links = 3.983874931
Mittlere Schienenlnge = 4.646783762
Totale Krmmung = 2.651635327 = 151.9275131¡
Mittlere Krmmung = 0.5706388468
Die mittlere
Schienenlnge entspricht nun der Trasselnge. Allerdings sieht das Gleisbild
immer noch etwas merkwrdig aus,
indem die innere Schiene einen Knick hat.
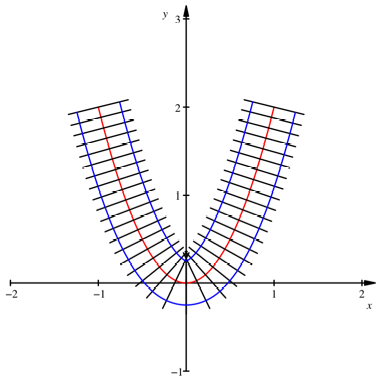
Innere Schiene hat einen
Knick
Wir verringern nun die
Spurweite auf ![]() .
.
Trasselnge = 4.646783762
Spurweite = 1/4
Schienenlnge rechts = 4.978238178
Schienenlnge links = 4.315329347
Mittlere Schienenlnge = 4.646783762
Totale Krmmung = 2.651635327 = 151.9275131¡
Mittlere Krmmung = 0.5706388468
Wir sehen, dass sich
die totale Krmmung nun nicht mehr ndert. Auch die innere Schiene sieht recht
ordentlich aus.
Verkleinerte Spurweite
3.2.2
Parallelkurven
Es ist nahe liegend,
die beiden Gleiskurven als Parallelkurven
zur ursprnglichen Kurve zu bezeichnen. Allerdings ist es so, dass diese
Parallelkurven in der Regel komplizierter sind als die ursprngliche Kurve. In
den obigen Beispielen sind die Gleiskurven keine Parabeln.
3.2.3
Lngenberechnungen
Die Lngenberechnungen
von Kurven fhren hufig zu Integralen, die formal nicht einfach zu bearbeiten
sind. Das gilt schon fr die ursprnglichen Kurven, insbesondere aber fr die
Parallelkurven, also die Gleiskurven. Man muss sich hier mit numerischer
Integration behelfen, was wiederum zu einem Verlust an Genauigkeit fhren kann.
3.3
Weitere Beispiele
3.3.1
Kreis
Beim Kreis ist die
totale Krmmung ![]() , und dies unabhngig vom Radius r. Beim Kreis sind die Parallelkurven ebenfalls
Kreise. Wenn wir die Spurweite mit
, und dies unabhngig vom Radius r. Beim Kreis sind die Parallelkurven ebenfalls
Kreise. Wenn wir die Spurweite mit ![]() bezeichnen,
erhalten wir fr die totale Krmmung
bezeichnen,
erhalten wir fr die totale Krmmung ![]() :
:
![]()
In dieses Umfeld gehrt
die Frage, um wie viel sich eine um die Erdkugel gelegte Schnur verlngert,
wenn wir sie berall einen Meter abheben, so wie die Zusatzfrage, wie sich das
auf dem Mond verhlt.
Fr die mittlere
Krmmung erhalten wir beim Kreis den vom Radius abhngigen Wert:
![]()
3.3.2
Ellipse
Eine totale Krmmung ![]() erhalten wir
allerdings auch bei deformierten Kreisen.
erhalten wir
allerdings auch bei deformierten Kreisen.
Als Beispiel eine
Ellipse:

Ellipse
Trasselnge = 19.37689644
Spurweite = 1/2
Schienenlnge rechts = 20.94769277
Schienenlnge links = 17.80610011
Mittlere Schienenlnge = 19.37689644
Totale Krmmung = 6.283185307 = 360.0¡
Mittlere Krmmung = 0.3242616962
Eigentlich versteht es
sich von selbst, dass alle einfach geschlossenen Kurven dieselbe totale
Krmmung ![]() wie der Kreis
haben. Nach einem Umlauf hat sich die Richtung ja um genau 360¡ verndert.
wie der Kreis
haben. Nach einem Umlauf hat sich die Richtung ja um genau 360¡ verndert.
3.3.3
Gleisoval
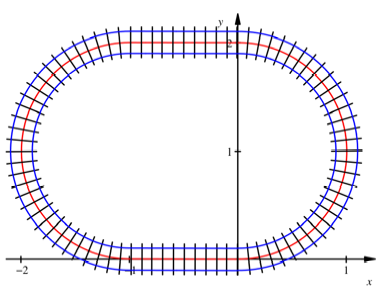
Gleisoval
Im klassischen der
Modelleisenbahn lsst sich wie beim Kreis ![]() elementar berechnen.
Der Krmmungsanteil der geraden Teilstcke ist null.
elementar berechnen.
Der Krmmungsanteil der geraden Teilstcke ist null.
3.3.4
Achterbahn
Bei einer Achterbahn
erhalten wir aus Symmetriegrnden die totale Krmmung null.
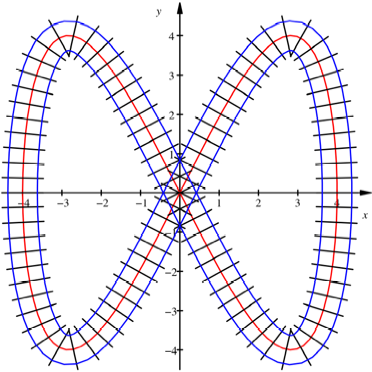
Achterbahn
Trasselnge = 37.71772519
Spurweite = 0.75
Schienenlnge rechts = 37.71772519
Schienenlnge links = 37.71772519
Mittlere Schienenlnge = 37.71772519
Totale Krmmung = 0 = 0¡
Mittlere Krmmung = 0
3.3.5
Doppelacht
Bei einer ãDoppelachtÒ
ergibt sich wieder die totale Krmmung ![]() .
.
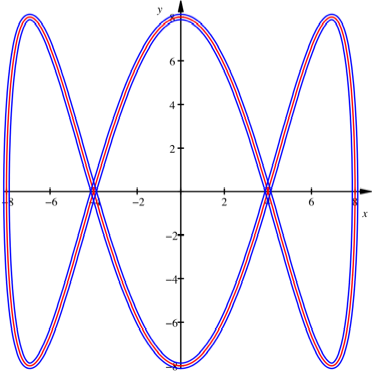
Doppelacht (Schwellen
nicht gezeichnet)
Trasselnge = 104.5233401
Spurweite = 0.25
Schienenlnge rechts = 105.3087383
Schienenlnge links = 103.7379419
Mittlere Schienenlnge = 104.5233401
Totale Krmmung = 6.283185307 = 360¡
Mittlere Krmmung = 0.06011274899
3.3.6
Schlinge
Bei einer Schlinge
ergibt sich ![]() .
.
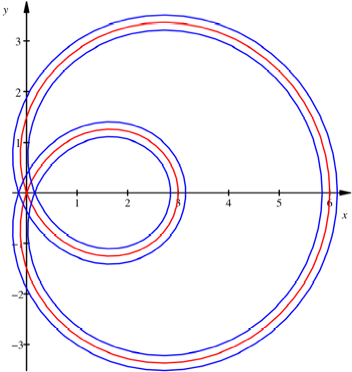
Schlinge
Trasselnge = 29.06534466
Spurweite = 0.3
Schienenlnge rechts = 30.95030025
Schienenlnge links = 27.18038907
Mittlere Schienenlnge = 29.06534466
Totale Krmmung = 12.56637061 = 720¡
Mittlere Krmmung = 0.4323489283
3.3.7
Kleeblatt
Beim Kleeblatt ergibt
sich ![]() .
.
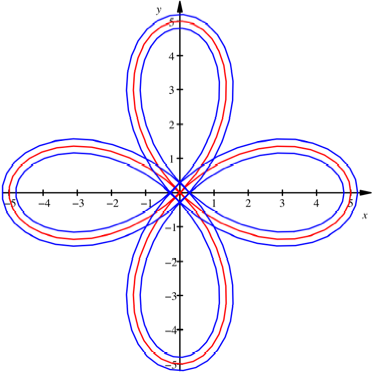
Kleeblatt
Trasselnge = 48.4422411
Spurweite = 0.4
Schienenlnge rechts = 52.21215229
Schienenlnge links = 44.67232992
Mittlere Schienenlnge = 48.4422411
Totale Krmmung = 18.84955592 = 1080¡
Mittlere Krmmung = 0.3891140354
Bei geschlossenen
Kurven ist offenbar die totale Krmmung ein Vielfaches von ![]() . Das ist anschaulich klar. Nach einem vollen Durchlauf
schaut die Lok wieder in derselben Richtung, hat sich also insgesamt um einen
Winkel gedreht, welche einem Vielfachen von
. Das ist anschaulich klar. Nach einem vollen Durchlauf
schaut die Lok wieder in derselben Richtung, hat sich also insgesamt um einen
Winkel gedreht, welche einem Vielfachen von ![]() entspricht.
entspricht.
3.3.8
Wendeschleife
Bei einer Wendeschleife
lsst sich elementar ![]() berechnen. Wir
haben einen Viertelkreis mit negativer Krmmung, welcher einen Viertelkreis mit
positiver Krmmung annulliert.
berechnen. Wir
haben einen Viertelkreis mit negativer Krmmung, welcher einen Viertelkreis mit
positiver Krmmung annulliert.
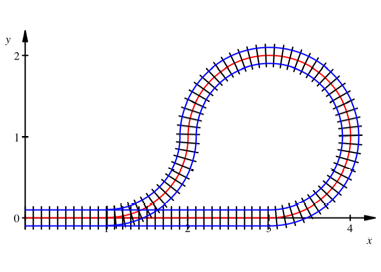
Wendeschleife
Das Programm ergibt
kleine Ungenauigkeiten in der Berechnung.
Trasselnge = 9.28
Spurweite = 0.2
Schienenlnge rechts = 9.59399552
Schienenlnge links = 8.966006066
Mittlere Schienenlnge = 9.280000793
Totale Krmmung = 3.13994727 = 179.9057265¡
Mittlere Krmmung = 0.3383563869
4
Von der mittleren Krmmung zur Momentankrmmung
Bei den bisherigen
Beispielen wurde, eher als Ballast, jeweils auch die mittlere Krmmung, also
die totale Krmmung dividiert durch die Trasselnge, angegeben.
Wenn wir die
Trasselnge sukzessive verkrzen, nhert sich die mittlere Krmmung einem
Grenzwert, der Momentankrmmung. Im
folgenden nennen wir diese Momentankrmmung einfach Krmmung.
4.1
Beispiel Parabel
4.1.1
Krmmung im Ursprung
Wir nehmen die Parabel ![]() des
Eingangsbeispieles und verkrzen sie durch
des
Eingangsbeispieles und verkrzen sie durch ![]() . Wir nhern uns also dem Scheitelpunkt im Ursprung.
. Wir nhern uns also dem Scheitelpunkt im Ursprung.
Fr ![]() erhielten wir
die Mittlere
Krmmung = 0.220966811.
erhielten wir
die Mittlere
Krmmung = 0.220966811.
Fr ![]() ergibt sich:
ergibt sich:
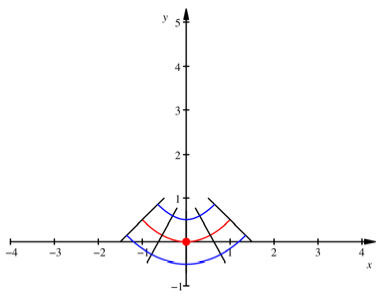
Verkrzte Parabel
Trasselnge = 2.295587149
Spurweite = 1
Schienenlnge rechts = 3.080985313
Schienenlnge links = 1.510188986
Mittlere Schienenlnge = 2.295587149
Totale Krmmung = 1.570796327 = 90¡
Mittlere Krmmung = 0.6842677819
Nun verkrzen wir
weiter:
![]() : Mittlere Krmmung =
0.9950306193
: Mittlere Krmmung =
0.9950306193
![]() : Mittlere Krmmung =
0.9999500031
: Mittlere Krmmung =
0.9999500031
![]() : Mittlere Krmmung =
0.9999995
: Mittlere Krmmung =
0.9999995
![]() : Mittlere Krmmung =
0.999999995
: Mittlere Krmmung =
0.999999995
Wir haben
offensichtlich den Grenzwert 1. Unsere Parabel hat mit Ursprung die Krmmung 1.
4.1.2
Krmmung im Punkt 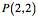
Fr ![]() ergibt sich:
ergibt sich:
Anderer Ausschnitt
Trasselnge = 4.504846145 = 0.7169685319*2*PI
Spurweite = 1
Schienenlnge rechts = 4.73666995
Schienenlnge links = 4.273022341
Mittlere Schienenlnge = 4.504846145
Totale Krmmung = 0.463647609 = 26.56505118¡
Mittlere Krmmung = 0.1029219632
Nun verkrzen wir
weiter:
![]() : Mittlere Krmmung =
0.0895680425
: Mittlere Krmmung =
0.0895680425
![]() : Mittlere Krmmung =
0.08944397131
: Mittlere Krmmung =
0.08944397131
![]() : Mittlere Krmmung =
0.08944273162
: Mittlere Krmmung =
0.08944273162
![]() : Mittlere Krmmung =
0.08944271923
: Mittlere Krmmung =
0.08944271923
Es zeichnet sich wieder
ein Grenzwert ab, aber ein anderer. Mit Methoden der Differenzialgeometrie kann
dieser Grenzwert exakt berechnet werden. Er ist ![]() .
.
Unsere Parabel hat im
Punkt ![]() die Krmmung
die Krmmung ![]() . Diese Krmmung ist kleiner als die Krmmung im Ursprung,
was auch anschaulich klar ist.
. Diese Krmmung ist kleiner als die Krmmung im Ursprung,
was auch anschaulich klar ist.
4.2
Definition der Krmmung
Um die Krmmung in einem Kurvenpunkt zu bestimmen, whlen wir ein
Kurvenstck, das diesen Punkt enthlt, und berechnen die mittlere Krmmung
dieses Kurvenstckes. Nun lassen wir das Kurvenstck zu unserem Punkt zusammenschrumpfen.
Der Grenzwert der mittleren Kurvenkrmmung ist die Krmmung in fokussierten
Kurvenpunkt.
4.2.1
Erinnerung an die Schule: Steigung
Um die Steigung in
einem Punkt auf einem Funktionsgrafen zu bestimmen, nehmen wir ein Kurvenstck
auf dem Funktionsgrafen, das diesen Punkt enthlt. Wir verbinden die Endpunkte
dieses Kurvenstckes mit einer Sehne. Die Steigung dieser Sehne ist die
mittlere Steigung des Kurvenstckes. Nun lassen wir das Kurvenstck zu unserem
Punkt zusammenschrumpfen. Der Grenzwert der mittleren Steigung ist die Steigung
in fokussierten Kurvenpunkt. Geometrisch ist des die Steigung der
Kurventangente in diesem Punkt.
4.3
Krmmung des Kreises
Wir arbeiten mit einem
Kreis mit Radius r. Wir haben oben schon
gesehen, dass seine mittlere Krmmung der Kehrwert ![]() ist.
ist.
Zur Bestimmung der
Krmmung in einem Kreispunkt arbeiten wir nun mit einem Kreissektor, der diesen
Punkt enthlt. Bei einem Sektorwinkel ![]() (im Bogenma§)
und der Spurweite
(im Bogenma§)
und der Spurweite ![]() ergeben sich die
Bogenlnge
ergeben sich die
Bogenlnge ![]() , die beiden Gleislngen
, die beiden Gleislngen ![]() und
und ![]() und somit die
totale Krmmung:
und somit die
totale Krmmung:
![]()
Fr die mittlere
Krmmung folgt daraus:
![]()
Diese mittlere Krmmung
hngt nur vom Radius r ab und ist
konstant fr alle Kreisbogen. Daher ist dies auch der Grenzwert.
Der Kreis mit Radius r hat also in jedem Punkt die Krmmung ![]() . Je gr§er der Radius, umso kleiner die Krmmung.
. Je gr§er der Radius, umso kleiner die Krmmung.
5
Visualisierung der Krmmung
Qualitativ sehen wir
sofort, wo eine Kurve stark gekrmmt ist und wo beinahe gerade. Es ist aber
— fr mich wenigstens — nicht einfach, den Wert der Krmmung in den
verschiedenen Kurvenpunkten abzuschtzen.
Die Krmmung kann aber
wie folgt visualisiert werden: Zunchst zeichnen wir die Kurve in eine x,y-Ebene. Dann tragen wir in jedem Kurvenpunkt die
Krmmung senkrecht dazu ab, also in den Raum hinein.
5.1
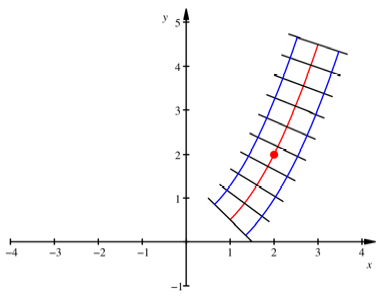
Beispiel Parabel
Wir nehmen wieder die
Parabel ![]() .
.
Krmmung der Parabel
Wir sehen, dass die
Krmmung im Scheitel am gr§ten ist und den Wert 1 hat und dann rasch abnimmt.
5.2
Weitere Beispiele
Wir visualisieren
einige der oben vorgestellten Beispiele.
5.2.1
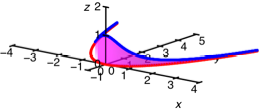
Kreis
Der Kreis hat die
Krmmung ![]() . Wir visualisieren im selben Bild die Krmmungen der Kreise
mit den Radien
. Wir visualisieren im selben Bild die Krmmungen der Kreise
mit den Radien ![]() .
.
Kreise mit verschiedenen
Radien
Obwohl alle Kreise
hnlich sind, ist dies bei den Krmmungsbildern nicht der Fall.
5.2.2
Ellipse
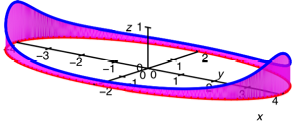
Ellipse
Die Krmmung ist in den
so genannten ãspitzen ScheitelnÒ m gr§ten. Die senkrechte magenta Flche
entspricht der totalen Krmmung ![]() .
.
5.2.3
Gleisoval
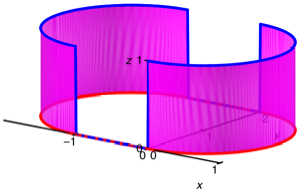
Gleisoval
Wir sehen die abrupten
Krmmungssprnge beim bergang von geraden zu gekrmmten Schienen. Das sind die
Orte, wo die Lok jeweils entgleist, wenn man zu scharf darber fhrt.
5.2.4
Achterbahn
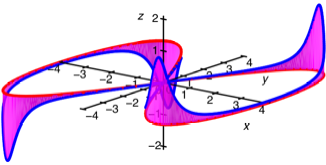
Achterbahn
Im linken Teil ist die
Krmmung negativ, daher ist die totale Krmmung null.
5.2.5
Doppelacht
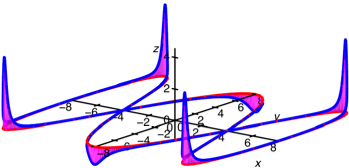
Doppelacht
Wir haben positive und
negative Krmmungen. Die positiven Krmmungen berwiegen. ![]() .
.
5.2.6
Schlinge
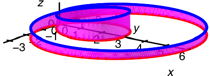
Schlinge
Nur positive
Krmmungen.
5.2.7
Kleeblatt
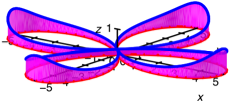
Kleeblatt
Nur positive
Krmmungen.
5.2.8
Wendeschleife
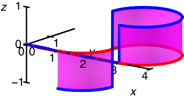
Wendeschleife
Wiederum
Krmmungssprnge.
6
Trassierung im Bauwesen
6.1
Die Klothoide
Um abrupte
Krmmungssprnge wie bei der aus Kreisbgen und Geradenstcken gebauten
Wendeschleife zu vermeiden, wird bei der Trassierung von Verkehrstrgern mit
Klothoidenbgen gearbeitet. Bei einer Klothoide wchst die Krmmung
gleichm§ig.
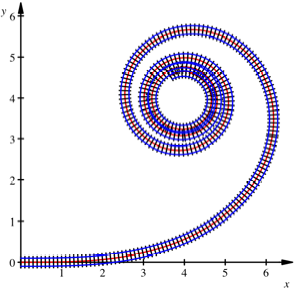
Klothoide
In der Visualisierung
sehen wir das gleichm§ige Wachstum der Krmmung.
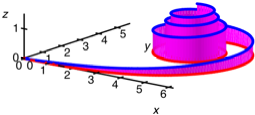
Klothoide
6.2
Zusammensetzung
Das Trasse ist
zusammengesetzt aus einem geraden Stck, einem Klothoidenbogen und einem
Kreisbogen.
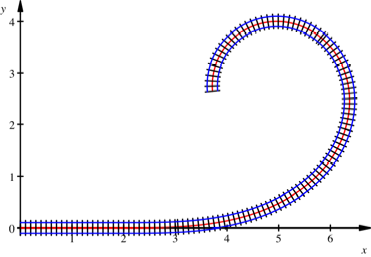
Zusammensetzung
Die stetige Vernderung
der Krmmung sehen wir in der Visualisierung.
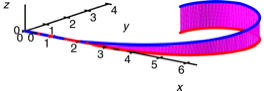
Stetige Vernderung der
Krmmung