Hans Walser, [20210320]
KrŸmmung
1 Worum geht es?
KrŸmmung
eines Funktionsgrafen 
.
Beispiele
2 Steigung und KrŸmmung
Die erste Ableitung 
gibt die Steigung an der Stelle x.
Der
Steigungswinkel 
ist dann:
(1)
Die zweite Ableitung 
gibt die €nderung der Steigung bei
Variation von x.
Die €nderung der WeglŠnge s bei €nderung von x ist nach Abbildung 1:
(2)
Abb. 1: €nderung der WeglŠnge
Aus (2) ergibt sich:
(3)
Die KrŸmmung 
ist die
€nderung des Steigungswinkels, also die RichtungsŠnderung,
bezogen auf den Weg. Eine gro§e KrŸmmung hei§t also eine gro§e
RichtungsŠnderung auf kleinem Weg (ãscharfe KurveÒ).
In Formeln:
(4)
Dabei wŠre es allerdings praktisch, wenn wir das in AbhŠngigkeit von x ausdrŸcken kšnnten.
Der Rest ist Rechnung. Erinnerung: Ableitung des arctan:
(5)
Aus (1) folgt zunŠchst mit der Kettenregel (die zweite Ableitung von f erscheint als sogenannte innere Ableitung):
(6)
Das ist aber nicht, was wir wollen. Wir wollen die Ableitung nach s. Also erneut die Kettenregel:
(7)
Wir setzen nun (6) und (3) in (7) ein. Das gibt:
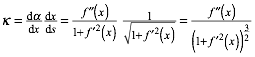(8)
In (8) ist die KrŸmmung in AbhŠngigkeit von x angegeben.
3 Beispiele
3.1 Quadratische Parabel
Aus
(9)
ergibt sich:
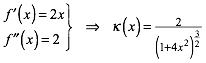(10)
Die KrŸmmung ist fŸr x = 0 am grš§ten. Wir haben dort den kleinsten KrŸmmungskreis. Der KrŸmmungskreisradius ist der Kehrwert des Betrages der KrŸmmung.
Die Abbildung 2 zeigt die Parabel mit den KrŸmmungskreisen.
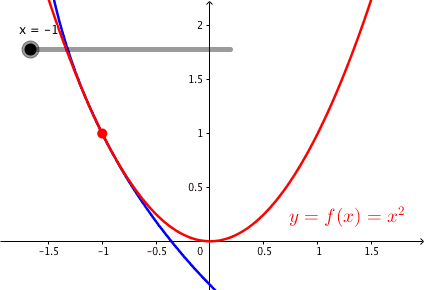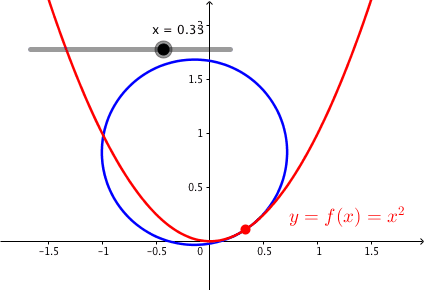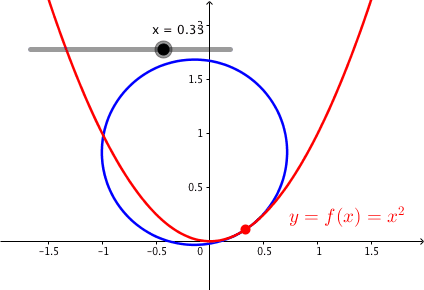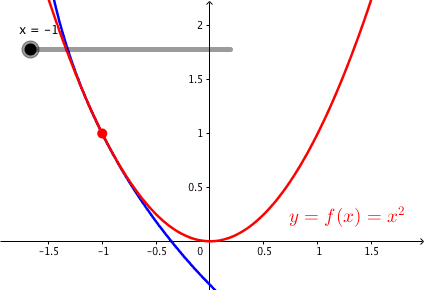
Abb. 2: Parabel und KrŸmmungskreise
3.2 Kubische Parabel
Aus
(11)
ergibt sich:
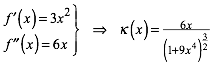(12)
FŸr x = 0 ist die KrŸmmung null und Šndert das Vorzeichen. Der KrŸmmungskreis hat einen unendlich gro§en Radius, ist also eine Gerade (die Wendetangente). Die €nderung des Vorzeichens bedeutet, dass wir bei wachsendem x einen †bergang von einer Rechtskurve (negative KrŸmmung) zu einer Linkskurve (positive KrŸmmung) haben.
Die Abbildung 3 zeigt die kubische Parabel mit den KrŸmmungskreisen.
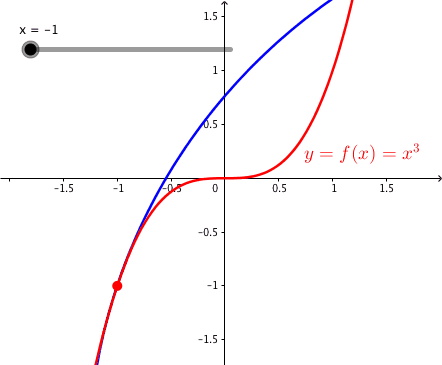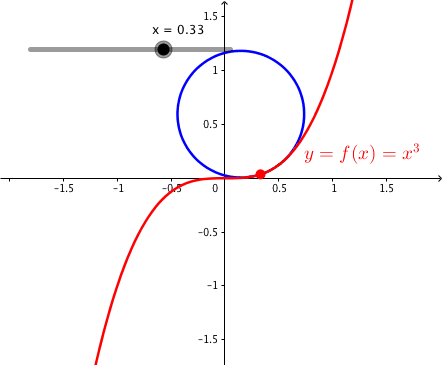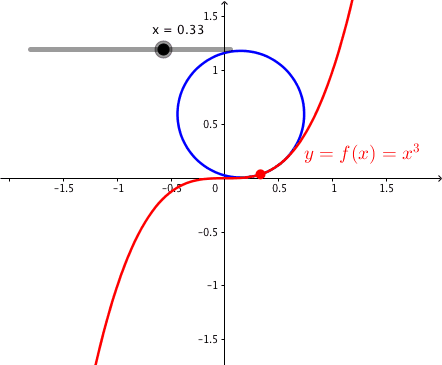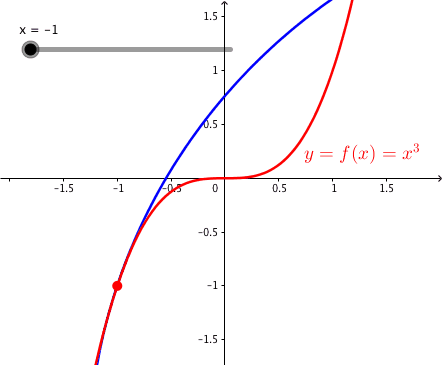
Abb. 3: Kubische Parabel und KrŸmmungskreise
Die Abbildung 4 zeigt ein weiteres Beispiel einer kubischen Parabel.
Abb. 4: Kubische Parabel
3.3 Parabel vierten Grades
Aus
(13)
ergibt sich:
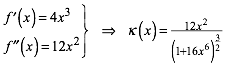(14)
FŸr x = 0 ist die KrŸmmung zwar null, aber sie Šndert nicht das Vorzeichen. Daher haben wir permanent eine Linkskurve. Die KrŸmmung hat bei x = 0 eine doppelte Nullstelle.
Der KrŸmmungskreis wird lokal bei x = 0 eine Gerade.
Die Abbildung 5 zeigt den Sachverhalt.
Abb. 5: Parabel vierten Grades
Mit dieser Parabel vierten Grades kann man folgendes illustrieren: in einem Wendepunkt ist die zweite Ableitung null. Das hei§t aber nicht, dass umgekehrt an jeder Nullstelle der zweiten Ableitung ein Wendepunkt sein muss. Unsere Parabel vierten Grades ist ein Gegenbeispiel dazu.
Das Verschwinden der zweiten Ableitung ist also eine notwendige, aber keine hinreichende Bedingung fŸr einen Wendepunkt.
3.4 Parabel sechsten Grades
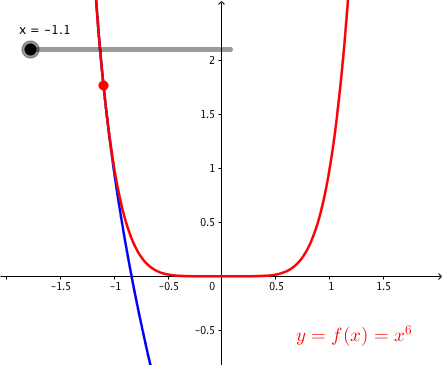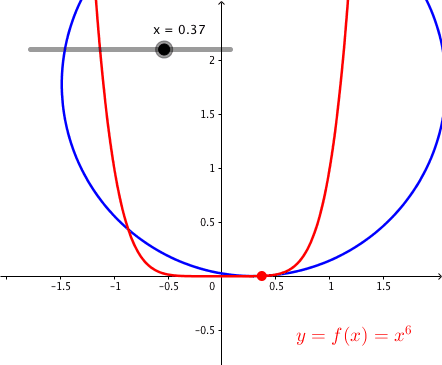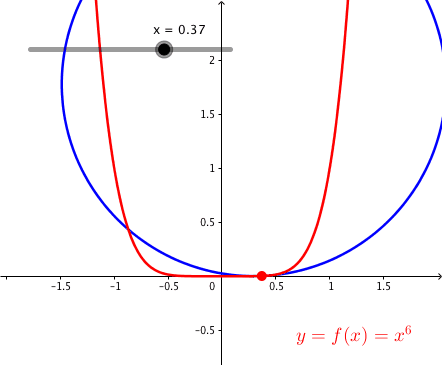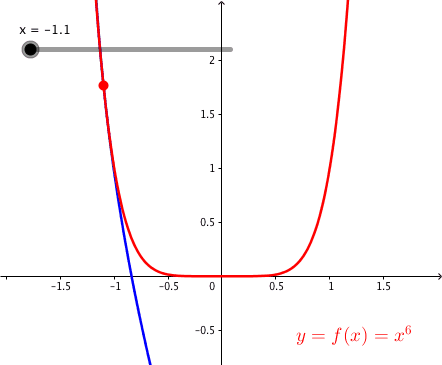
Abb. 6: Parabel sechsten Grades
Websites
Hans Walser: KrŸmmung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kruemmung/Kruemmung.htm
Hans Walser: KrŸmmungen
http://www.walser-h-m.ch/hans/Miniaturen/K/Kruemmungen/Kruemmungen.htm
Hans Walser: KrŸmmung am Beispiel
http://www.walser-h-m.ch/hans/Miniaturen/B/Beispiel_zur_Kruemmung/Beispiel_zur_Kruemmung.htm
Hans Walser: KrŸmmung der KrŸmmung
http://www.walser-h-m.ch/hans/Miniaturen/K/Kruemmung_der_Kruemmung/Kruemmung_der_Kruemmung.htm