Hans Walser, [20100120a]
KrŸmmung der KrŸmmung
1
Idee
Zu einer Funktion 
sei 
, 
die KrŸmmung des
Funktionsgrafen von 
, und allgemein 
die KrŸmmung des
Funktionsgrafen von 
. Wir iterieren also die KrŸmmung. Ob das mathematische oder
sonstwie sinnvoll ist, bleibe dahingestellt. Lustig ist es allemal.
2
Programm
MuPAD-Programm, am
Beispiel fŸr 
.
f:=x->x^2:
// Funktion
N:=2:
// Obergrenze
a:=-3:
// untere Intervallgrenze
b:=3:
// obere Intervallgrenze
k[0]:=f:
for n from 1 to N do
k[n]:=k[n-1]''/((1+(k[n-1]')^2)^(3/2)):
end_for:
kurve:=n->plot::Curve2d([x, float(k[n](x))], x=a..b,
LineWidth=1/2, LineColor=[1-n/N,0,n/N], Mesh=100*n+100):
plot(kurve(n)$n=0..N,
Scaling=Constrained, TicksDistance=1, TicksBetween=0,
ViewingBox=[a..b,-3..3], AxesLineWidth=0.5,
AxesTitleFont=["Times", 12, Italic],
TicksLabelFont=["Times", 12],
Width=140, Height=140)
Die Obergrenze 
gibt an, dass wir die Ÿbliche KrŸmmung (
) und die KrŸmmung des Diagramms der Ÿblichen KrŸmmung bearbeiten
und plotten.
Der Farbcode geht nach
ãje blauer desto krummÒ. Rot ist die Ausgangsfunktion, blau die letzte der
berechneten KrŸmmungsfunktionen.
Im Beispiel des
Programms erhalten wir:
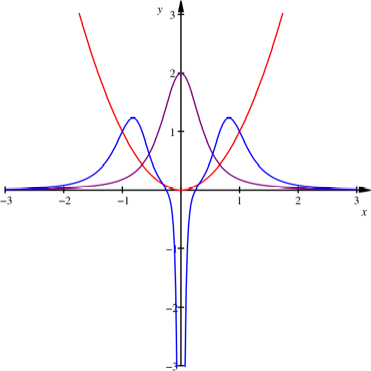
Quadratfunktion,
KrŸmmung, KrŸmmung der KrŸmmung
3
Beispiele
Bildergalerie mit
einigen Beispielen
3.1
Exponentialfunktion
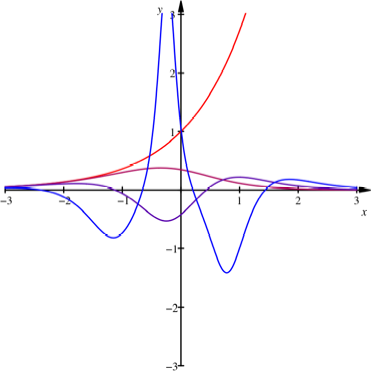
Exponentialfunktion
3.2
Oberer Halbkreis
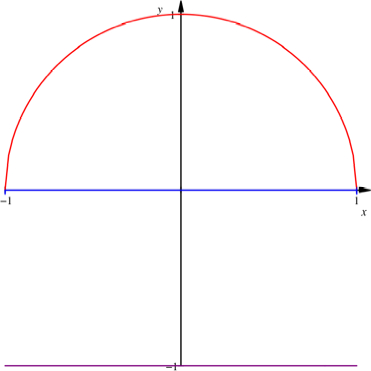
Oberer Halbkreis
Nun ja, das war zu
erwarten.
3.3
Glockenkurve der Normalverteilung
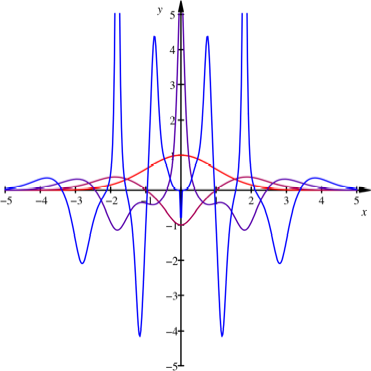
Glockenkurve
3.4
Arcustangens
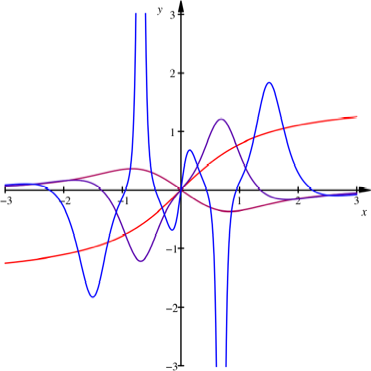
Arcustangens