Hans Walser, [20160619]
Krummer Pythagoras
1 Rechtwinklige Dreiecke
Die Abbildung 1a zeigt ein rechtwinkliges Dreieck mit dem Thaleskreis.
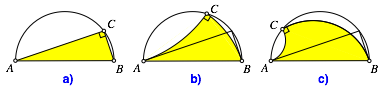
Abb. 1: Rechtwinklige Dreiecke
Wenn wir die Ecke C auf dem Thaleskreis bewegen, bleibt zwar der rechte Winkel invariant, aber die spitzen Winkel bei A und B verŠndern sich.
Wenn wir diese spitzen Winkel bei A und B ebenfalls invariant lassen wollen, mźssen wir die Katheten verbiegen.
Die Abbildungen 1b und 1c zeigen zwei solche verbogene rechtwinklige Dreiecke, welche bei A und B dieselben Winkel haben wie das Dreieck der Abbildung 1a. Die Katheten sind Kreisbšgen.
2 Satz des Pythagoras
Die Abbildung 2 illustriert den źblichen Satz des Pythagoras. Die rote QuadratflŠche ist gleich gro§ wie die Summe der beiden hellblauen QuadratflŠchen.
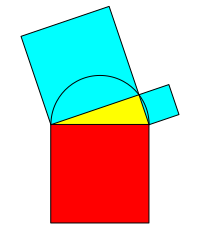
Abb. 2: Rot = Hellblau
Die Abbildung 3 zeigt das Entsprechende fźr die krummen rechtwinkligen Dreiecke.
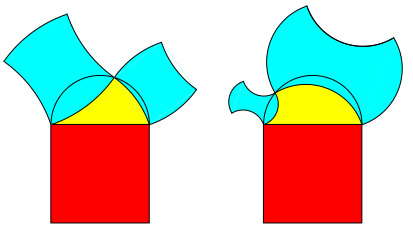
Abb. 3: Rot = Hellblau
Die Bogenvierecke haben kongruente Seiten und rechte Winkel. Beim rechten Dreieckswinkel haben wir glatte †bergŠnge.
Die FlŠchengleichheit rot = hellblau stimmt immer noch. Warum?
Die Abbildung 4 zeigt Zerlegungsbeweise nach Perigal.
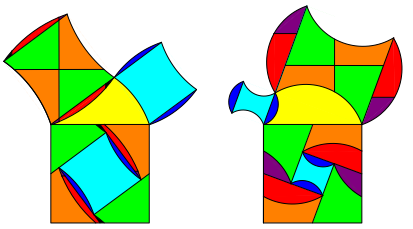
Abb. 4: Zerlegungsbeweise