Hans Walser, [20181209a]
Kubikzahlen
Visuelle Bearbeitung einer Aufgabe von Thomas Jahre, Chemnitz
1 Worum geht es?
1³ = 1 = 1
2³ = 8 = 3 + 5
3³ = 27 = 7 + 9 + 11 (1)
4³ = 64 = 13 + 15 + 17 + 19
5³ = 125 = 21 + 23 + 25 + 27 + 29
Und?
2 Die ungeraden Zahlen

Abb. 1: Ungerade Zahlen
Die ungeraden Zahlen können als Winkel visualisiert werden (Abb. 1).
Die Zahl 1 entspricht dem kleinen roten Quadrat links.
Die Zahl 3 entspricht drei in einem Winkel angeordneten hellblauen Quadraten.
Die Zahl 5 entspricht fünf in einem Winkel angeordneten gelben Quadraten.
Und so weiter.
3 Gruppierung

Abb. 2: Gruppierung
Wir gruppieren die Winkel in Gruppen von je 1, 2, 3, 4, 5, ... Winkeln. In der Abbildung 2 sind die Gruppen abwechslungsweise rot-grün und hellblau-gelb dargestellt. Die Gruppengrenzen sind mit dicken schwarzen Linien gezeichnet.
Durch diese Gruppierung erhalten wir dicke Winkel mit den Schenkelbreiten 1, 2, 3, 4, 5, ... .
4 Umfärben

Abb. 3: Umfärben
Wir färben innerhalb jeder Gruppe (also in jedem dicken Winkel) um, so dass gleichfarbige Quadrate und an den Enden allenfalls halbe Quadrate entstehen (Abb. 3). Die Anzahlen der kleinen Quadrate in den beiden Farben einer Gruppe werden dabei verändert, die Gesamtzahl der kleinen Quadrate bleibt aber unverändert. Vgl. Nelsen (2000), S. 85.
5 Einbettung in den Raum

Abb. 4: Wir gehen in den Raum
6 Trennung der dicken Winkel

Abb. 5: Trennung der dicken Winkel
Jeder dicke Winkel ist aus n quadratischen Platten (allenfalls zwei halbe Platten) der Kantenlänge n zusammengesetzt.
7 Zerschneiden und Aufstapeln
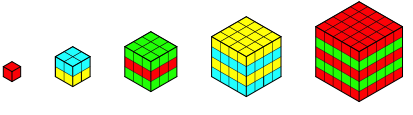
Abb. 6: Zerschneiden und Aufstapeln
Wir zerschneiden die dicken Winkel in diese Platten und stapeln diese aufeinander.
So entstehen Würfel der Kantenlänge n. Damit ist (1) illustriert.
Literatur
Nelsen, Roger B. (2000): Proofs without Words. MAA, The Mathematical Association of America. ISBN 978-0883857007
Weblink
Hans Walser: Summenformel
www.walser-h-m.ch/hans/Miniaturen/S/Summenformel/Summenformel.htm