1 Mitte zweier Nullstellen

Bei der Besprechung der Nullstellenbestimmung nach dem Approximationsverfahren von Newton-Raphson stellt sich im Unterricht die Frage, zu welcher Nullstelle ein gewählter Startwert führt.

Um dies auszutesten, wählte Jürg genau das arithmetische Mittel zweier Nullstellen einer kubischen Parabel als Startwert. Zu seinem und auch meinem Erstaunen führte gleich der erste Approximationsschritt exakt zur dritten Nullstelle.

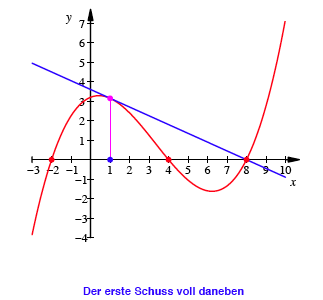
Was steckt dahinter?

2 Verallgemeinerung

Statt mit einer Tangente können wir auch mit Sekanten arbeiten.

Die kubische Parabel habe die Nullstellen , , . Die Parabel hat also die Gleichung:

Ferner sei das arithmetische Mittel zweier Nullstellen, zum Beispiel:

Nun wählen wir zwei Werte, welche symmetrisch zu (und damit auch zum Nullstellenpaar , ) liegen, also:

und

Schließlich sei die Sektante durch die beiden Parabelpunkte und . Dann verläuft diese Sekante durch die dritte Nullstelle, das heißt durch den Punkt .

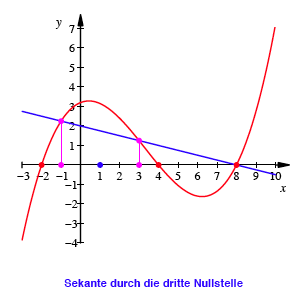
Für den Grenzfall erhalten wir den oben geschilderten Sonderfall mit der Tangente.

3 Beweis

Den Beweis organisieren wir rückwärts, indem wir mit einer Geraden durch die dritte Nullstelle beginnen und dann die Schnittpunkte mit der Parabel berechnen. Die Gerade hat die Gleichung:

Schnitt mit der Parabel führt auf:

Eine Lösung dieser kubischen Gleichung ist natürlich . Für die anderen beiden Lösungen dividieren wir durch den zugehörigen Linearfaktor und erhalten die quadratische Gleichung:

Diese hat die beiden Lösungen:

und

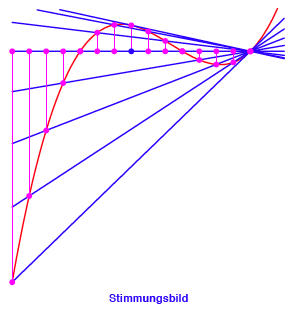
Diese beiden Lösungen liegen tatsächlich symmetrisch zu .

4 Schwerpunkt aller drei Nullstellen

Für ergibt sich mit der Wendepunkt der kubischen Parabel.

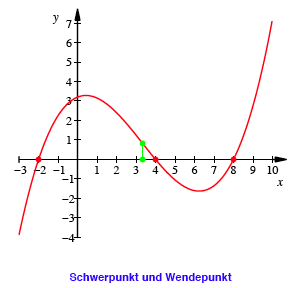
Beweis: Wir müssen die zweite Ableitung null setzen:

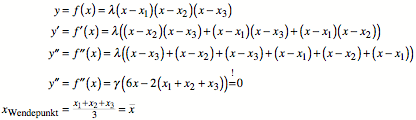
Literatur

[Kalman 2008] Kalman, Dan: The Most Marvelous Theorem in Mathematics. Math HORIZONS, Published by the Mathematical Association of America. 16 April 2008. P. 16-17