1 Worum es geht

Punktsymmetrie der kubischen Parabel

2 Beispiel

Die Abbildung 1 zeigt eine kubische Parabel mit ihrem Wendepunkt.

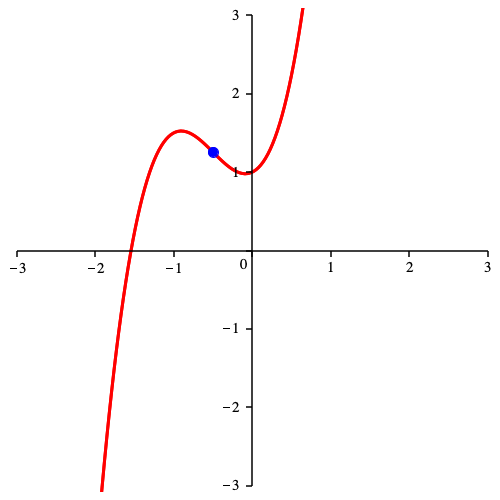
Ein Bild, das Diagramm, Reihe enthält.

Automatisch generierte Beschreibung

Abb. 1: Kubische Parabel mit Wendepunkt

Der Wendepunkt ist Symmetriezentrum (Abb. 2).

Abb. 2: Punktsymmetrie

Dies gilt allgemein für kubische Parabeln.

3 Beweis

Die kubische Parabel mit der Gleichung

y = a*x^3 + b*x^2 + c*x + d

hat den Wendepunkt W:

W = [-b/(3*a), (2*b^3)/(27*a^2) - c*b/(3*a) + d]

Mit der Variablentransformation

x := u - b/(3*a)

y := v + (2*b^3)/(27*a^2) - c*b/(3*a) + d

wird der Ursprung in den Wendepunkt verschoben. Die kubische Parabel erhält die Gleichung:

v = a*u^3 + (c - b^2/(3*a))*u

Wir haben in u nur noch Terme ungeraden Grades. Die zugehörige Kurve (die kubische Parabel) ist daher punktsymmetrisch bezüglich des Ursprungs (also des Wendepunktes der kubischen Parabel). Dies war zu zeigen.

Weblinks

Hans Walser: Kubische Parabel

http://www.walser-h-m.ch/hans/Miniaturen/K/Kubische_Parabel/Kubische_Parabel.htm

Hans Walser: Kubische Kreuzparabel

http://www.walser-h-m.ch/hans/Miniaturen/K/Kubische_Kreuzparabel/Kubische_Kreuzparabel.html