Hans Walser, [20191126]
Kuboktaeder-Kantenmodell
1 Worum geht es?
Es wird ein Kantenmodell des Kuboktaeders
vorgestellt. Als Baumaterial dienen Rechtecke aus Papier mit dem Seitenverhltnis
![]() . Fr
jede Kante braucht es ein Papier, die Bauteile reprsentieren die Kanten des
Modells.
. Fr
jede Kante braucht es ein Papier, die Bauteile reprsentieren die Kanten des
Modells.
2 Das Kuboktaeder
Wenn wir bei einem Wrfel alle Ecken bis zur Kantenmitte hin abschneiden entsteht ein Kuboktaeder (Abb. 1a).
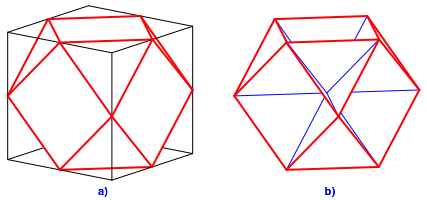
Abb. 1: Kuboktaeder
Die Oberflche des Kuboktaeders besteht aus sechs Quadraten und acht gleichseitigen Dreiecken. Der Umkugelradius ist gleich gro§ wie die Kantenlnge. Wir knnen jede der zwlf Ecken mit dem Mittelpunkt verbinden und erhalten so eine Figur aus 24 gleichseitigen Dreiecken (Abb. 1b). Im Mittelpunkt treffen sich die Spitzen von acht hohlen Tetraedern und sechs hohlen Pyramiden, welche je ein halbes hohles Oktaeder sind.
Unser Kantenmodell besteht nun aus 24 doppelwandigen gleichseitigen Dreiecken, welche alle eine Spitze im Mittelpunkt haben. Fr jedes Dreieck brauchen wir ein Bauteil.
3 Bauteil
Jedes der
24 Bauteile entsteht aus einem Papierrechteck mit dem Seitenverhltnis ![]() (Abb. 2a).
In den Abbildungen ist aus didaktischen Grnden ein Papier angenommen, das auf
der Vorderseite hellblau und auf der Rckseite gelb ist. Papierstrke etwa 70-90
g/m2.
(Abb. 2a).
In den Abbildungen ist aus didaktischen Grnden ein Papier angenommen, das auf
der Vorderseite hellblau und auf der Rckseite gelb ist. Papierstrke etwa 70-90
g/m2.
Wir legen eine Faltschablone mit denselben Ausma§en aus etwas strkerem Papier diagonal darber (Abb. 2b). Es ist egal, welche der beiden Diagonalen wir whlen, aber wir mssen es bei allen Bauteilen gleich machen.
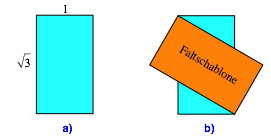
Abb. 2: Rechteck und Faltschablone
Nun falten wir die vorstehenden Ecken des Papiers ber die Faltschablone (Abb. 3). Die beiden Papierecken treffen sich genau in der Mitte der Faltschablone (warum?).
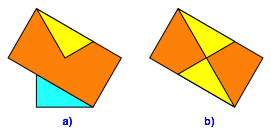
Abb. 3: Ecken einfalten
Die Faltschablone knnen wir nun herausziehen (Abb. 4a). Es entsteht ein Rhombus der aus zwei gleichseitigen Dreiecken besteht.
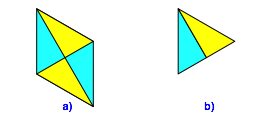
Abb. 4: Fertigstellung des Bauteils
Nun
falten wir den einen Teil des Rhombus nach hinten (Abb. 4b). Diese letzte
Faltkante wird dann zu einer Kante des Kuboktaeders. Wir haben nun ein Bauteil mit zwei
Verbindungslaschen (gelb in Abb. 4b) zum Einschieben in die Nachbarteile. Eine
Verbindungslasche ist vorn, die andere hinten.
Die Abbildung 5 zeigt zwei Ansichten eines Bauteils.


Abb. 5: Bauteil
4 Zusammenbau
Und nun kommt das Interessante, der Zusammenbau. Wir schieben jeweils
eine Verbindungslasche zwischen die beiden gleichseitigen Dreiecke des
Nachbarbauteils. Es empfiehlt sich, den Zusammenbau zunchst schrittweise mit Broklammern
zu fixieren. An jeder Ecke des Kuboktaeders hat es dann vier Broklammern, da
an jeder Ecke vier Kanten zusammenkommen. Wenn alles sitzt, knnen die
Broklammern schrittweise entfernt und durch eine Heftklammer mit dem Tacker
ersetzt werden. Dabei hat man den Ehrgeiz, dass die Klammern symmetrisch
eingebracht werden. Die Abbildungen 6 und 7 zeigen das fertige Modell. Es ist
ãdnnÒ und hat kein Volumen. In der Abbildung 6 steht das Modell auf einem
Vierkant-Trichter (wie bei der Abb. 1b). Entsprechend haben wir auch oben einen
Vierkant-Trichter. Er hat eine Pyramidenform, mit der Spitze nach unten.

Abb. 6: Modell
In der Abbildung 7 steht das Modell auf einem Dreikant-Trichter. Er hat
die Form eines regelm§igen Tetraeders.

Abb. 7: Andere Position des Modells
5 Farben
In den Abbildungen 8 bis 10 wurde mit farbigen Bauteilen gearbeitet. Es sind je sechs Bauteile in den Farben orange, gelb, lila und hellblau. Da an jeder Ecke des Modells vier Bauteile zusammenkommen, kann man es so einrichten, dass sich an jeder Ecke zwei Farben kreuzen.
In der Abbildung 8 steht das Modell auf einem Vierkant-Trichter (wie bei
den Abb. 1b und 6). Entsprechend haben wir auch oben einen Vierkant-Trichter.
Er hat eine Pyramidenform, mit der Spitze nach unten. Jede Seitenflche des Vierkant-Trichters
hat eine andere Farbe.

Abb. 8: Farbiges Modell
In der Abbildung 9 steht das Modell auf einem Dreikant-Trichter (analog
Abb. 7). Er hat die Form eines regelm§igen Tetraeders.

Abb. 9: Andere Position
In der Abbildung 10 wurde die Situation der Abbildung 9 so aufgenommen, dass wir alle orangen Bauteile sehen. Sie bilden ein regelm§iges Sechseck.

Abb. 10: Regelm§iges Sechseck
Insgesamt haben wir vier regelm§ige Sechsecke in unserer Figur, je eins in jeder Farbe.
6 Farbkombinatorik
Bei jeder Vierseit-Pyramide kommen alle vier Farben vor, aber jedes Mal in einer andren zyklischen Reihenfolge. In der Abbildung 8 ist oben sichtbar die zyklische Reihenfolge orange-gelb-lila-hellblau.
Bei vier
Farben gibt es ![]() zyklische
Reihenfolge (Abb. 11). In unserem Modell kommt jede dieser sechs zyklischen
Reihenfolgen genau einmal vor.
zyklische
Reihenfolge (Abb. 11). In unserem Modell kommt jede dieser sechs zyklischen
Reihenfolgen genau einmal vor.

Abb. 11: Zyklische Reihenfolgen von vier Farben
Bei jedem
Tetraeder kommen drei der vier Farben vor. Dazu gibt es ![]() Mglichkeiten.
Zu jeder Mglichkeit gibt es zwei zyklische Reihenfolgen (Abb. 12). Wir haben
also insgesamt acht Flle. In unserem Modell kommt jeder dieser acht Flle
genau ein Mal vor.
Mglichkeiten.
Zu jeder Mglichkeit gibt es zwei zyklische Reihenfolgen (Abb. 12). Wir haben
also insgesamt acht Flle. In unserem Modell kommt jeder dieser acht Flle
genau ein Mal vor.
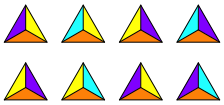
Abb. 12: Farbverteilungen bei den Tetraedern
An jeder
der zwlf Ecken des Modells sehen wir zwei sich kreuzende Farben. Das gibt
zunchst ![]() Mglichkeiten.
Die zugehrigen Sechsecke schneiden sich unter dem kristallografischen Winkel:
Mglichkeiten.
Die zugehrigen Sechsecke schneiden sich unter dem kristallografischen Winkel:
![]() (1)
(1)
Unter Bercksichtigung des (von au§en gesehenen) Drehsinns gibt es nun zwlf Mglichkeiten (Abb. 13). In unserem Modell kommt jeder dieser zwlf Flle genau ein Mal vor.

Abb. 13: Situationen an den Ecken
Websites
Hans Walser: Kantenmodell des Wrfels und des Tetraeders
www.walser-h-m.ch/hans/Miniaturen/K/Kantenmodell_Wuerfel/Kantenmodell_Wuerfel.htm