Hans Walser, [20220706]

Kuboktaeder-Stern

Idee und Anregung: Maik Bleckmann, Bremen

1 Worum geht es

Auf der Basis des Würfels wird zunächst ein Kuboktaeder hergestellt und dieses zu einem Stern ausgebaut. Clusterbildung. Verschiedene Sichten.

2 Das Kuboktaeder

Wenn wir bei einem Würfel alle Ecken bis zur Kantenmitte hin abschneiden entsteht ein Kuboktaeder (Abb. 1).

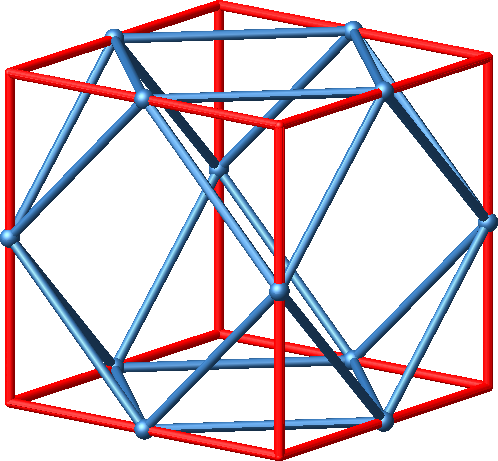
Abb. 1: Kuboktaeder

Das Kuboktaeder ist die Schnittfigur eines Würfels (Kubus) mit einem Oktaeder, daher der Doppelname (Abb. 2).

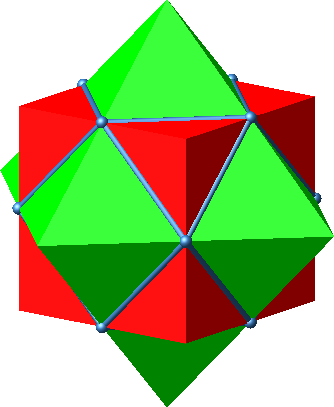
Abb. 2: Schnittfigur

Wir können jede der zwölf Ecken des Kuboktaeders mit dem Mittelpunkt verbinden und erhalten so eine Figur aus 24 gleichseitigen Dreiecken (Abb. 3 und 4). Im Mittelpunkt treffen sich die Spitzen von acht hohlen Tetraedern und sechs hohlen Pyramiden, welche je ein halbes hohles Oktaeder sind.

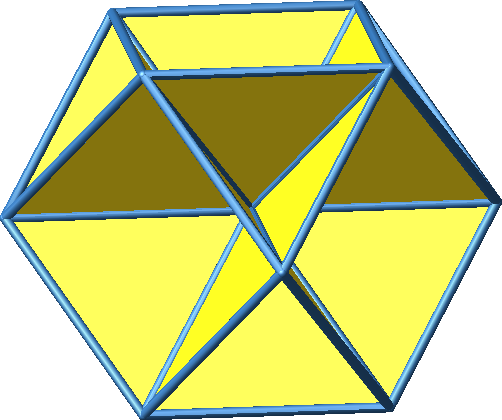
Abb. 3: Gleichseitige Dreiecke

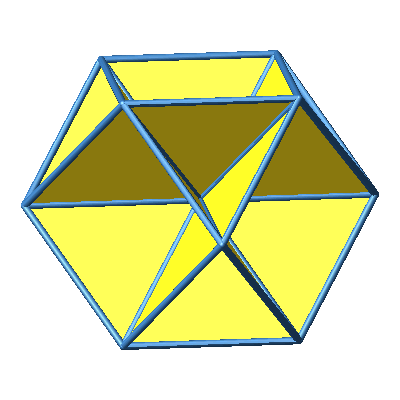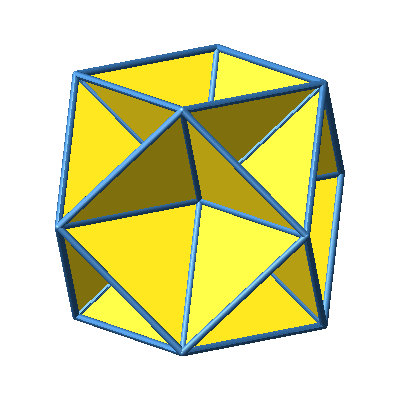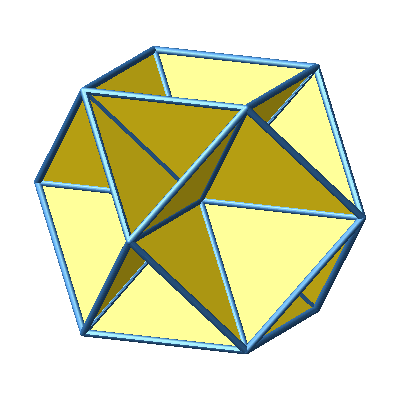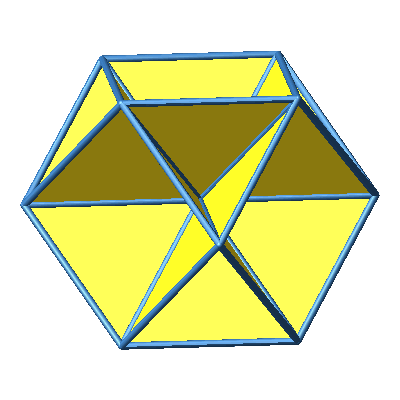
Abb. 4: Kuboktaeder mit gleichseitigen Dreiecken

Die Abbildung 5 zeigt ein Papiermodell des Kuboktaeders (Bauanleitung hier).

Abb. 5: Papiermodell

3 Vom Kuboktaeder zum Stern

Durch Zusammenfügen von zwei gleichseitigen Dreiecken entsteht ein Rhombus mit spitzen Winkeln von 60° (Abb. 6).

Abb. 6: Rhombus

Wir setzen nun den gleichseitigen Dreiecken der Abbildungen 4 und 5 nach außen je ein gleichseitiges Dreieck an. Dadurch entsteht ein Stern aus 24 Rhomben mit entsprechend 24 Spitzen (Abb. 7 und 8). Wir nennen diesen Stern den Kubolkaeder-Stern.

Abb. 7: Kuboktaeder-Stern aus 24 Rhomben

Abb. 8: Kuboktaeder-Stern

Die Abbildung 9 zeigt das Kantengerüst des Kuboktaeder-Sterns ohne die Rhombenflächen.

Abb. 9: Kantengerüst des Kuboktaeder-Sterns

4 Spezielle Sichten

Die Abbildung 10a zeigte eine allgemeine Sicht auf einen Würfel. Es gibt nun aber drei spezielle Sichten auf einen Würfel.

(1) Wir können frontal auf eine Seitenfläche schauen (Abb. 10b). Der Umriss der Figur ist ein Quadrat.

(2) Wir können den Würfel über eine Kante ansehen (Abb. 10c). Der Umriss der Figur ist ein Rechteck im Seitenverhältnis des DIN-Formates. Wir sehen zwei Seitenflächen, die als Rechtecke im DIN-Format erscheinen.

(3) Wir können den Würfel über eine Ecke ansehen (Abb. 10d). Der Umriss der Figur ist ein regelmäßiges Sechseck. Wir sehen drei Seitenflächen, die als Rhomben mit einem spitzen Winkel 60° erscheinen.

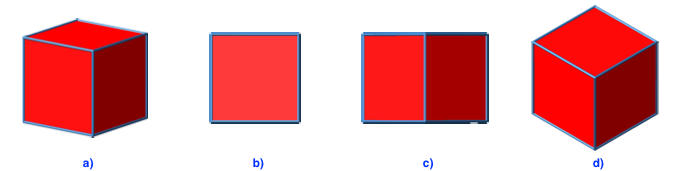
Abb. 10: Spezielle Sichten auf einen Würfel

Da das Kuboktaeder und damit der Kuboktaeder-Stern auf einem Würfel basieren (Abb. 1). Können wir den Kuboktaeder-Stern ebenfalls in den entsprechenden drei speziellen Sichten darstellen.

Die Abbildung 11 zeigt das Kantengerüst in frontaler Sicht. Der Umriss ist ein Stern mit acht Spitzen, allerdings sind die Kantenlängen der Spitzen nicht alle gleich groß. Rein planimetrisch gesehen, ist die Figur aus 16 rechtwinklig gleichschenkligen Dreiecken zusammengesetzt. Sie hat die Symmetrien eines Quadrates.

Abb. 11: Frontale Sicht

Die Abbildung 12 entspricht der Sicht über eine Würfelkante. Die Figur hat die Symmetrien eines Rechteckes.

Abb. 12: Merkwürdige Symmetrie

Die Abbildung 13 entspricht der Sicht über eine Würfelecke. Die Figur hat planimetrisch gesehen die Symmetrie eines regelmäßigen Sechseckes.

Abb. 13: Symmetrie des regelmäßigen Sechseckes

5 Cluster

Die Abbildung 14 zeigt eine würfelförmige Anordnung von 3×3×3 = 27 Kuboktaeder-Sternen in verschiedenen Ansichten.

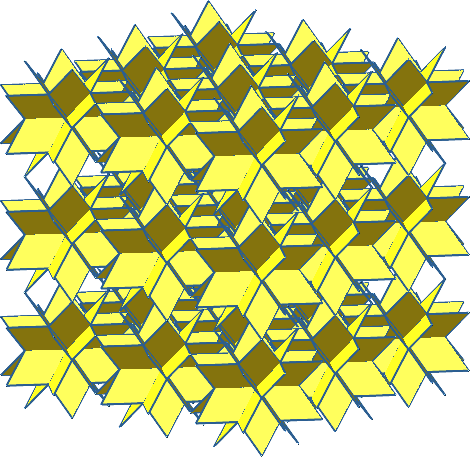
Abb. 14.1: Cluster

Abb. 14.2: Frontale Ansicht

Abb. 14.3: Sicht über eine Würfelkante

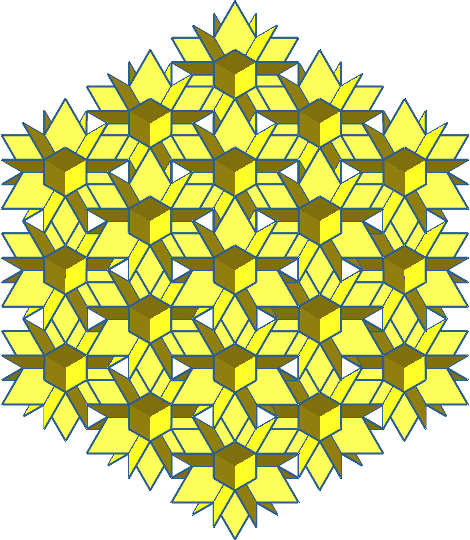
Abb. 14.4: Sicht über eine Würfelecke

Die Abbildung 15 zeigt dasselbe ohne Rhombenflächen, also nur mit den Kantengerüsten.

Abb. 15.1: Kantengerüst

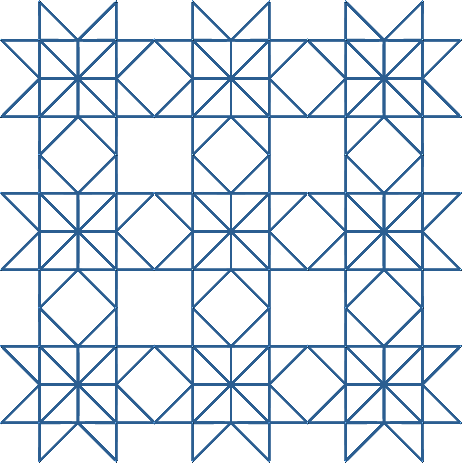
Abb. 15.2: Frontale Ansicht

Abb. 15.3: Sicht über Würfelkante

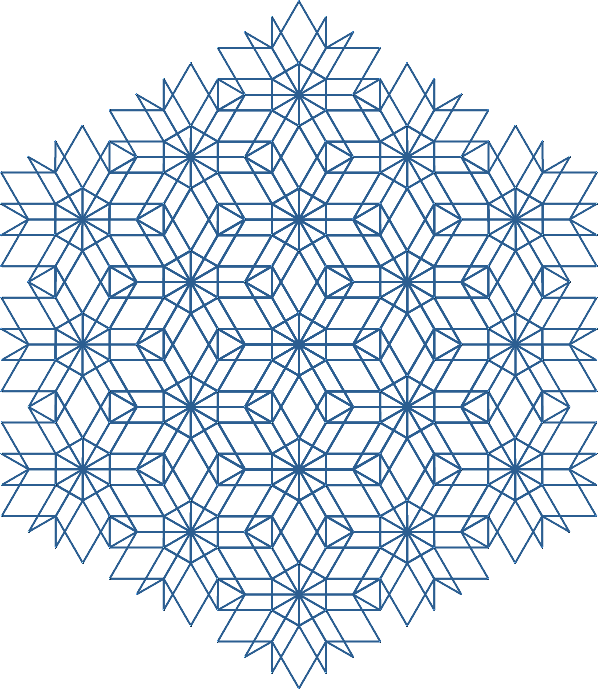
Abb. 15.4: Sicht über Würfelecke

Websites

Hans Walser: Kuboktaeder-Kantenmodell

http://www.walser-h-m.ch/hans/Miniaturen/K/Kuboktaeder-Kantenmodell/Kuboktaeder-Kantenmodell.htm

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.