Hans Walser, [20180114]

1 Kürzeste Würfelwege

1.1 Symmetrisches Beispiel

1.1.1 Der Tunnelweg

Auf dem Würfel der Abbildung 1a sind der Mittelpunkt einer Kante und der Mittelpunkt einer Seitenfläche markiert. Der Würfel habe die Kantenlänge 1.

Der kürzeste Verbindungsweg der beiden Punkt ist natürlich der Tunnel durch den Würfel (Abb. 1b).

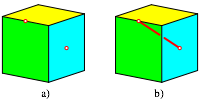
Abb. 1: Der kürzeste Weg ist ein Tunnel

Frage 1: Wie lang ist der Tunnel?

1.1.2 Auf der Würfelfläche

Die Abbildung 2a zeigt einen kürzesten Verbindungsweg auf der Würfelfläche. Den Übergangspunkt über die Kante kann aus der Abwicklung (Abb. 2b) entnommen werden.

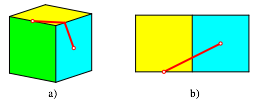
Abb. 2: Ein kürzester Weg auf der Würfeloberfläche

Frage 2: Wie lang ist dieser Weg?

Wenn wir den Übergangspunkt über die Würfelkante etwas variieren, wird der Weg länger (Abb. 3a). Dies wird aus der Abwicklung (Abb. 3b) sofort ersichtlich. Der blaue Weg ist länger als der rote Weg.

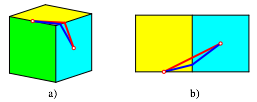
Abb. 3: Variation des Übergangspunktes

Frage 3: In der Bildlegende zur Abbildung 2 ist von „einem“ kürzesten Weg die Rede. Warum dieser unbestimmte Artikel?

Frage 4: Gibt es einen kürzesten Weg hinten herum? Wenn ja, wie lang ist dieser?

1.2 Asymmetrisches Beispiel

Die Abbildung 4 zeigt ein asymmetrisches Beispiel eines kürzesten Weges auf der Würfeloberfläche. Der eine Punkt ist immer noch die Seitenmitte, die Position des anderen ergibt sich durch die Rasterung. Die Weglänge ist .

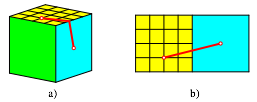
Abb. 4: Asymmetrisches Beispiel

Die Abbildung 5 zeigt einen anderen Weg. Dieser Weg hat die Länge . Er ist somit länger als der Weg der Abbildung 4. Trotzdem ist er kürzer als alle Wege, die sich durch eine Variation der Übergangspunkte auf der jeweiligen Würfelkante ergeben. Er ist also lokal kürzester Weg, aber nicht global.

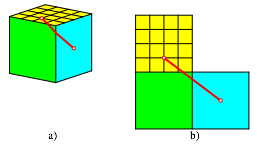
Abb. 5: Variante

Frage 5: Was kann über die beiden Wege der Abbildung 6 gesagt werden?

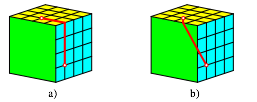
Abb. 6: Vergleich der Wegelängen

Frage 6: Wie viele kürzeste Wege gibt es von einem Seitenflächenmittelpunkt eines Würfels zu seinem diametral gegenüberliegenden Punkt?

Frage 7: Wie viele kürzeste Wege gibt es von einer Würfelecke zur diametral gegenüberliegenden Würfelecke?

Frage 8: Wie ist es im allgemeinen Fall: Kürzester Weg von einem Punkt auf der Würfeloberfläche zum diametral gegenüberliegenden Punkt?

1.3 Gleiche Winkel

Bei den (lokal) kürzesten Wegen läuft dieser in der Abwicklung geradlinig über die Kanten. Somit ist der Auftreffwinkel auf eine Kante jeweils gleich dem Abgangswinkel von der Kante (Abb. 7).

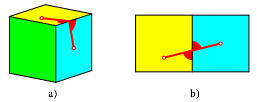
Abb. 7: Gleiche Winkel

Ein analoges Phänomen haben wir etwa beim Billard, nur läuft dort der Weg wieder zurück ins gleiche Quadrat.

Wege auf der Würfeloberfläche welche die Kanten in der Abwicklung geradlinig schneiden, werden auch als geodätische Linien oder kurz Geodätische bezeichnet. Dabei ist zu unterscheiden zu einer „Geodäten“. Dies ist eine weibliche Person, welche sich der Geodäsie, also der Vermessungs- und Kartenkunde widmet.

1.4 Geschlossene Wege auf dem Würfel

1.4.1 Beispiele

Geschlossene Wege, also geschlossene geodätische Linien, ergeben sich durch Verschnüren des Würfels (Abb. 8).

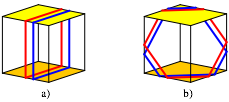
Abb. 8: Geschlossene Wege

Geschlossene Wege lassen eine lokale Parallelverschiebung auf den Würfelseiten zu. Dabei kann der Gesamtweg seine Form verändern (Abb. 8b). Die Gesamtlänge bleibt aber invariant. Was auf der einen Seite der Kante verloren geht, erscheint als Zugewinn auf der anderen Seite.

1.4.2 Rationale Steigung und Geschlossenheit

Eine geodätische Linie schneidet die Würfelkanten immer unter einem der beiden Winkeln oder . Unter der Steigung m der geodätischen Linie verstehen wir den Wert .

Wir markieren auf einer geschlossenen geodätischen Linie einen beliebigen Punkt und wickeln längs dieser geodätischen Linie ab, bis der markierte Punkt ein zweites Mal erscheint (Abb. 9).

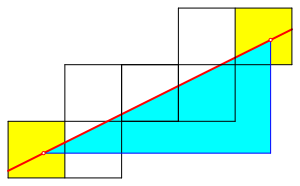
Abb. 9: Abwickeln längs des Weges

Dann hat das Steigungsdreieck ganzzahlige Katheten. Die Steigung m ist also rational.

Ein geschlossener Weg hat also notwendig eine rationale Steigung. Das heißt aber auch, dass es zu einer irrationalen Steigung keinen geschlossenen Weg geben kann. So ist es zum Beispiel nicht möglich, dass ein geschlossener Weg die Würfelkanten unter Winkeln von 60° oder 30° schneidet, da der Tangens dieser Winkel irrational ist.

Umgekehrt kann es bei einer rationalen Steigung Probleme geben. Wenn wir etwa in einem Seitenmittelpunkt mit dem Winkel 45°, also mit , starten, fahren wir auf eine Ecke zu und wissen dort nicht mehr weiter. In diesem Fall muss der Startpunkt leicht verschoben werden.

1.5 Bearbeitung der Fragen

Bearbeitung der Frage 1: Bei der Kantenlänge 1 des Würfels hat der Tunnel die Länge . Das ist gleich lang wie die Höhe im gleichseitigen Dreieck der Seitenlänge 1 (Abb. 51).

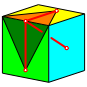
Abb. 51: Vergleich mit Dreieckshöhe

Bearbeitung der Frage 2: Der Weg hat die Länge . Am besten wird das auf Grund der Abwicklung gerechnet.

Bearbeitung der Frage 3: Es gibt noch eine zweite Lösung, die gleich lang ist (Abb. 52a). Sie entsteht durch eine andere Abwicklung (Abb. 52b).

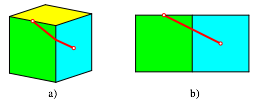
Abb. 52: Zweite Lösung

Wir haben also zwei kürzeste Lösungen. Sie sind kürzer als jede Lösung, die sich durch Variation des Übergangspunktes ergeben.

Bearbeitung der Frage 4: Die Abbildung 53a zeigt eine Lösung hinten herum. Die Übergangspunkte über die Kanten können in der begleitenden Abwicklung gefunden werden. Der Weg hat die Länge .

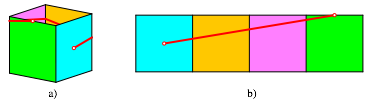
Abb. 53: Hinten herum

Die Abbildung 54 zeigt einen Zickzack-Weg im vorderen (grünen) Seitenquadrat, der durch dieselben Übergangspunkte festgelegt ist. Der Zickzack-Weg verläuft im Quadrat wie bei einem Billard.

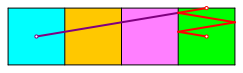
Abb. 54: Billard-Lösung

Es gibt noch viele andere Lösungen. So können wir etwa mehrfach um den Würfel herumwickeln.

Bearbeitung der Frage 5: Die beiden Wege haben die gleiche Länge ist (Abb. 55).

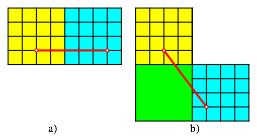
Abb. 55: Gleich lange Wege

Bearbeitung der Frage 6: Die einfachste Lösung läuft orthogonal über die Kanten (Abb. 56). Diese Wege haben die Länge 2.

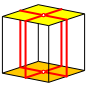
Abb. 56: Kürzeste Wege zum gegenüberliegenden Punkt

Es gibt allerdings weitere Lösungen, welche lokal, das heißt im Vergleich mit Nachbarkurven, kürzeste Wege darstellen. Die Abbildung 57a zeigt ein Beispiel der Länge . Der Weg liegt nicht in einer Ebene, wie aus der Ergänzung zum geschlossenen Weg (Abb. 57c) ersichtlich ist. .

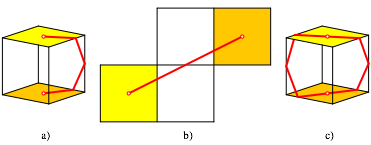
Abb. 57: Lokal kürzester Weg

Die Abbildung 58 zeigt ein umfangreiches, sich selbst überkreuzendes Beispiel mit der fortgesetzten Abwicklung.

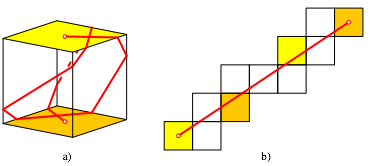
Abb. 58: Umfangreiches Beispiel

Bearbeitung der Frage 6: Die Abbildung 59a zeigt eine der sechs möglichen absolut kürzesten Verbindungen. Diese sechs kürzesten Wege sind die Kanten einer Sechskant-Doppelpyramide (Abb. 59b). Es gibt weitere nur noch relativ kürzeste Wege zwischen zwei diametralen Eckpunkten (Abb. 59c).

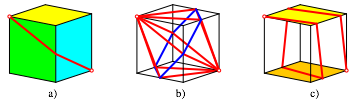
Abb. 59: Von Ecke zu Ecke

Bearbeitung der Frage 7: Die Abbildung 60 zeigt unterschiedliche Lösungen mit den zugehörigen Abwicklungen.

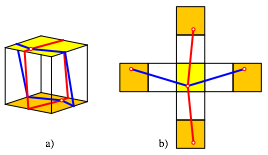
Abb. 60: Unterschiedliche Lösungen