Hans Walser, [20090824a]

Kugel-Steckmodelle

1 Worum geht es?

Es werden Steckmodelle von Kugeln besprochen. Dabei werden Großkreise, in Einzelfällen auch Kleinkreise, aus starkem Papier geschnitten, geschlitzt oder gekerbt und zusammengesteckt. Allgemeines über Steckmodelle siehe [Walser 2009].

2 Großkreismodelle

2.1 Kugelmodell mit drei Großkreisen

Durch Projektion des Oktaeders auf seine Umkugel erhalten wir drei paarweise orthogonale Großkreise.

Oktaeder und Projektion auf die Umkugel

2.1.1 Einfachstes Modell

Steckmodell mit drei Großkreisen

Wir verwenden drei verschiedene Bauteile.

Bauteile

Für das Zusammenstecken werden die Bauteile in der Reihenfolge von links nach rechts eingebaut. Beim Zusammenstecken ist ein wenig sanfte Gewalt nötig — eine Übung in Feinmotorik.

2.1.2 Die Versuchung

An sich (was immer „an sich“ heißt) käme man mit drei Exemplaren des mittleren Bauteils aus.

Drei gleiche Bauteile?

Wir bräuchten also nur einen Bauteiltyp. Es müsste dann einfach der rote Bauteil durch den grünen gesteckt werden, der grüne durch den blauen und der blaue durch den roten. Ausprobieren! — Der erste Schritt geht problemlos, aber dann kommen wir in Schwierigkeiten. Die drei Bauteile sind topologisch gesehen Ringe, welche wie die drei borromäischen Ringe wechselseitig ineinander verschlungen sein müssten.

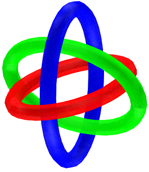
Drei borromäische Ringe

Drei nicht verschlungene Ringe können wir aber nur in die borromäische Lage bringen, indem wir einen der drei Ringe aufschneiden und nach dem Zusammenfügen wieder zusammenlöten. So machen es die Zauberkünstler mit ihren acht Ringen...

2.1.3 Gleiche Bauteile

Allerdings geht es mit gleichen Bauteilen. Allerdings müssen wir die Kreise sozusagen halbieren. Wir brauchen daher sechs Bauteile.

Modell mit sechs gleichen Bauteilen

Bauteilmuster:

Bauteil

2.1.4 Beliebiges sphärisches Dreieck

Unser Modell unterteilt die Kugeloberfläche in acht kongruente sphärische Dreiecke, deren Seitenlängen (auf der Einheitskugel) je sind, und die drei rechte Winkel haben.

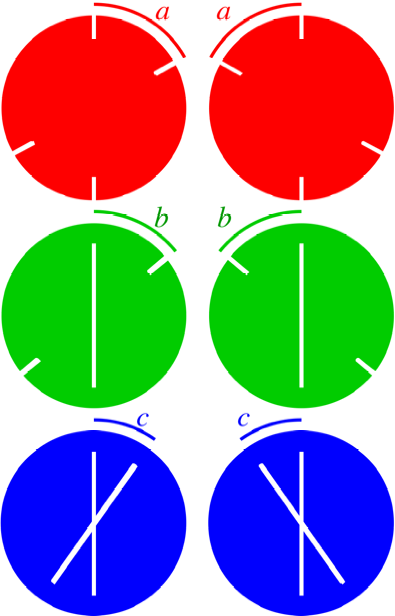
Wir bauen nun eine Kugel mit einem beliebigen sphärischen Dreieck mit den Seitenlängen a, b, c (bezogen auf die Einheitskugel mit dem Umfang 2π). Wir können entweder mit drei Kreisbauteilen arbeiten oder mit drei Paaren von Halbkreisbauteilen.

Bei drei Kreisscheiben ist die Topologie dieselbe wie beim einfachsten Modell oben.

Drei Kreisscheiben

Im Anhang das Beispiel in extenso. Es ist auch eine spiegelbildliche Version angegeben. Die Idee dabei ist, das Beispiel auf einem Farbdrucker auszudrucken, auszuschneiden und dann die gleichfarbenen Bauteile zweiseitig zu verwenden. Ein Zusammenkleben ist nicht einmal nötig, die Teile halten durch das Zusammenstecken.

Bei drei Paaren von Halbkreisbauteilen kann das so aussehen:

Halbkreis-Bauteile

In der folgenden Abbildung ist das fragliche sphärische Dreieck oben.

Sphärisches Dreieck

Dieses Modell ist geeignet, um die Herleitung der Flächenformel mit dem sphärischen Exzess zu visualisieren.

2.2 Kugelmodell mit vier Großkreisen

Durch Projektion des Kuboktaeders auf seine Umkugel erhalten wir die Situation der folgenden Abbildung. Die Kugeloberfläche wird durch vier Großkreise in acht sphärische Dreiecke und sechs sphärische Vierecke unterteilt.

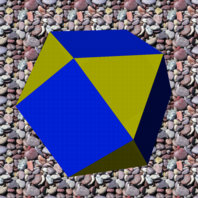
Kuboktaeder und Projektion auf die Umkugel

2.2.1 Einfaches Modell

Kugelmodell des Kuboktaeders

Wir benötigen vier Bauteile gemäß Figur:

Bauteile

Für das Zusammenstecken werden die Bauteile in der Reihenfolge von links nach rechts eingebaut.

2.2.2 Modell mit gleichen Bauteilen

Zwölf gleiche Bauteile

Der einzelne Bauteil ist im Prinzip (Winkelabstand zwischen den äußersten Kerben) ein Drittelskreis.

Bauteil

Da wir vier Großkreise haben, brauchen wir also zwölf gleiche Bauteile.

2.3 Kugelmodell mit sechs Großkreisen

Wir projizieren das Ikosidodekaeder auf seine Umkugel.

Ikosidodekaeder und Projektion auf Umkugel

Dies führt zu einer Figur mit sechs Großkreisen.

An sich ist es möglich, ein Modell mit sechs Teilen zu bauen.

Modell aus sechs Teilen

Die Teile sind ungleich.

Bauteile

Das Zusammenstecken ist äußerst heikel, besonders das Einbringen des letzten Bauteils ist etwa vergleichbar mit der Erdumsegelung des Ferdinand de Magellan. Es empfiehlt sich daher, insbesondere bei den letzten Bauteilen, mit zwei Hälften zu arbeiten.

Halbierte Bauteile

Äußerlich sieht man das dem Modell nicht an.

Ikosidodekaeder

3 Die geografische Kugel

3.1 Meridiane und Breitenkreise

Modell mit einer 30°-Rasterung.

Meridiane und Breitenkreise

Blick auf den Südpol

Für die Meridiane brauchen wir 12 Bauteile, welche paarweise aus sechs Typen bestehen.

Bauteile für die Meridiane

Der zweite und der sechste Bauteil sind symmetrisch, ebenso der dritte und der vierte. Wenn wir mit beidseitig gleichfarbenem Papier arbeiten, können wir diese Teile zusammenfassen. Bei der Verwendung von Fotos unter Berücksichtigung der beiden Seiten sind die Teile verschieden.

Die Bauteile finden sich großformatig im Anhang.

Für den Äquator brauchen wir 2 Bauteile, für die Breitenkreise ±30° insgesamt vier Bauteile und ebenso für die Breitenkreise ±60°.

Bauteile für Äquator und Breitenkreise

Für die Herstellung der Bauteile habe ich mit Kartonschablonen gearbeitet. Die Schablone wird auf die Rückseite der Foto gelegt und mit Kugelschreiber übertragen.

Die Schablone links kann für alle 6 Typen von Meridianen verwendet werden, dazu dienen die Führungslöcher auf der Achse.

Schablonen für die Bauteile

Das Zusammenstecken beginnt mit den Meridianen an der Erdachse. Die zwei gleichen Bauteile ergänzen sich zu einem Großkreis. Anschließend werden die Bauteile für Äquator und Breitenkreise eingesteckt.

3.2 Meridianebenen und Breitenkegel

Wir ersetzen die Breitenkreisebenen durch Breitenkreiskegel mit Spitze im Kugelzentrum und dem Breitenkreis als Leitkreis. Das Modell ist geeignet, die Kugelkoordinaten zu erklären. Auch Punkte im Kugelinnern haben die „richtige“ geografische Breite. Modell mit einer 30°-Rasterung.

Meridianebenen und Breitenkegel

Sicht auf den Nordpol

Für die Meridiane brauchen wir 12 Bauteile, welche paarweise aus sechs Typen bestehen.

Bauteile für die Meridiane

Bauteile für Äquator und Breitenkegel

Die Bauteile für Äquator und Breitenkegel haben alle denselben Radius, hingegen sind die Winkelabstände der Kerben verkürzt.

Für den Äquator brauchen wir zwei der Bauteile links, für die Breitenkegel ± 30° insgesamt vier der Bauteile Mitte und für die Breitenkegel ± 60° insgesamt zwei der Bauteile rechts, da dieser Bauteil den ganzen Kegelmantel (inklusive Überlappungen an den Nähten) darstellt.

4 Technisches

Die Bauteile sind aus starkem Papier geschnitten; dabei können alte Fotos, Ansichtskarten oder Karteikarten zweitverwertet werden. Das Ende einer Kerbe wird mit einer Lochzange durchgestoßen. Dann kann sehr einfach bis zum Ende mit der Scheren oder einem Japanschneider geschnitten werden. Die Breite der Kerben hängt vom verwendeten Material ab. Ich habe mit ca. 1 mm gearbeitet. Eine kerbenbreite ist zwingend, wenn man nur mit einem Schnitt arbeitet, wellt sich das Material.

Der Zusammenbau braucht keinen Klebestoff; die Modelle sind im Prinzip reversibel. Erfahrungen im Unterricht zeigen, dass die Technik leicht verständlich ist.

Literatur

[Walser 2009] Walser, Hans: Steckmodelle. MU Der Mathematikunterricht. Polyeder im Mathematikunterricht. Jahrgang 55. Heft 1. Februar 2009. Friedrich Verlag, Seelze. S. 38-47

Anhang

Sphärisches Dreieck mit Seiten a, b, c.

Kugel mit Meridianen und Breitenkreisen

Im folgenden Schnittmuster in Originalgröße für eine Kugel mit dem Radius ca. 7cm. Diese Größe ist geeignet für die Verwendung von DIN A6 Karteikarten oder alten Fotos im selben Format.

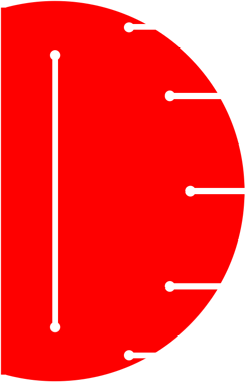
Meridian Typ 1

Meridian Typ 2

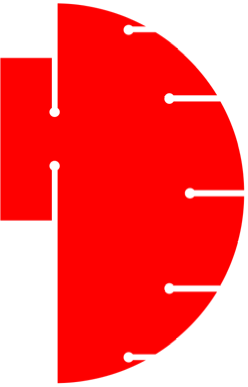
Meridian Typ 3

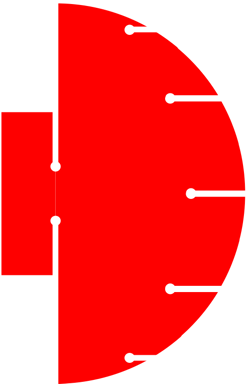
Meridian Typ 4

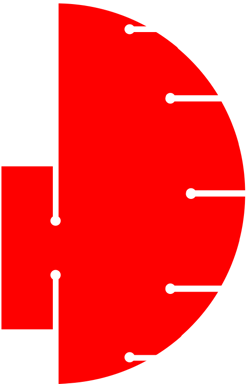
Meridian Typ 5

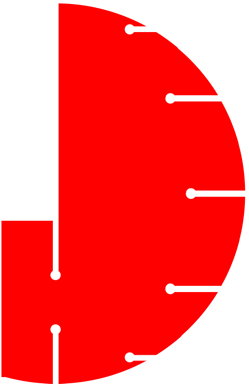
Meridian Typ 6

Äquator

Breitenkreis für ± 30°

Breitenkreis für ± 60°