[HW1]Hans Walser, [20110903a]
Kugeln als Baumaterial
1
Worum geht es?
Es werden einige bekannte Figuren als Kugelpackungen dargestellt. Dabei wird die dichteste Kugelpackung verwendet. Statt Kugeln kšnnen auch Rhombendodekaeder verbaut werden.
Bei Berechnungen arbeiten
wir mit Einheitskugeln, also 
.
2
Einfachste Kugelpackung
Die zum Beschreiben
einfachste Kugelpackung besteht aus Kugeln, deren Zentren ein WŸrfelgitter
bilden.
Sieben mal sieben mal
sieben Kugeln
Wenn wir die vorstehenden
Kugelteile abschruppen, erhalten wir einen WŸrfel.
Abgeschruppt.
Minimalmodell
Diese Kugelpackung hat
relativ viel Hohlraum. Im Minimalmodell sehen wir acht Achtelkugeln, insgesamt
also eine Kugel, eingepackt in einen WŸrfel der SeitenlŠnge 2. FŸr den
AusnŸtzungsgrad erhalten wir:
Fast die HŠlfte ist
Hohlraum.
3
Beste Kugelpackung
Eine bessere (die best
mšgliche) RaumausnŸtzung haben wir bei den im folgenden beschriebenen
Kugelpackungen. Der AusnŸtzungsgrad ist:
Die Herleitung des
AusnŸtzungsgrades folgt spŠter.
3.1 Tetraeder
3.1.1
Tetraeder als Kugelpackung
Die folgende Abbildung
zeigt ein Tetraeder mit 7 Kugeln lŠngs einer Kante.
Dreiecksbasis. Tetraeder
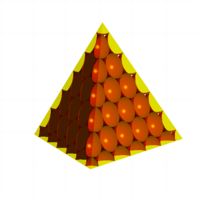
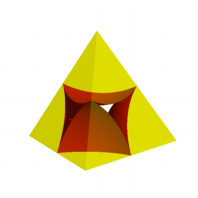
Abgeschruppt.
Minimalmodell
Das Minimalmodell des
Tetraeders ist allerdings nicht sehr geeignet, den AusnŸtzungsgrad zu
berechnen. Die vier angeschnittenen Kugelteile lassen sich nicht zu einem
ãschšnenÒ Kugelteil zusammenfŸgen.
3.1.2
Anzahl Kugeln
Wie viele Kugeln
enthŠlt ein Tetraeder mit n lŠngs einer
Kante?
In der untersten
Schicht bilden die Kugeln ein Dreieck der KantenlŠnde n.
Unterste Schicht
Die Anzahl 
der Kugeln ist:
FŸr die Anzahl 
der Kugeln im
Tetraeder erhalten wir daher (Induktion):
3.1.3
Rhombendodekaeder
Die Voronoi-Regionen
der (unendlich gro§ gedachten) Kugelpackung ist das Rhombendodekaeder. Das
Rhombendodekaeder ist von zwšlf kongruenten Rhomben mit dem DiagonalenverhŠltnis
berandet. In der
Position der folgenden Abbildung ist der Umriss, von oben gesehen, ein
Sechseck.
Rhombendodekaeder
Die folgende Abbildung
zeigt die in Rhombendodekaeder verpackten Kugeln des Tetraeders.
Tetraeder aus
Rhombendodekaedern
Die folgende Abbildung
zeigt die unterste Schicht, genau von oben gesehen.
Unterste Schicht
Es fŠllt schwer, das
von WŸrfeln zu unterscheiden.
3.2
Pyramide
3.2.1
Pyramide als Kugelpackung
Die Abbildung zeigt
eine Pyramide mit quadratischer Grundseite. Wir haben 
Kugeln sowohl an
den Grundkanten wie an den SchrŠgkanten.
Aufbau der Pyramide
3.2.2
Anzahl Kugeln
FŸr die Anzahl 
der Kugeln
finden wir:
3.2.3
Rhombendodekaeder
Die Rhombendodekaeder
mŸssen jetzt anders im Raum ausgerichtet sein. Der Umriss ist, von oben
gesehen, ein Quadrat.
Andere Ausrichtung des
Rhombendodekaeders
Damit lŠsst sich die
Pyramide bauen.
Pyramide aus
Rhombendodekaedern
Die unterste Schicht
von oben:
Kšlsch
3.3
Oktaeder
Die Pyramide ist
sozusagen ein halbes Oktaeder.
3.3.1
Oktaeder als Packungen von Kugeln und Rhombendodekaedern
Oktaeder
Die einzelnen
Rhombendodekaeder sind natŸrlich gleich orientiert wie bei der Pyramide
3.3.2
Anzahl Kugeln
FŸr die Anzahl 
der Kugeln
finden wir:
3.3.3
Link mit dem Tetraeder
Wir markieren die
mittlere Kugel auf jedem der acht Seitendreiecke des Oktaeders abwechslungsweise
mit magenta und cyan. Eine solche mittlere Kugel gibt es allerdings nur fŸr 
, also fŸr 
. Es hat dann vier magenta und vier cyan Kugeln. Die vier
magenta Kugeln sind Ecken eines regelmŠ§igen Tetraeders, ebenso natŸrlich die
cyan blauen Kugeln. Nun zerschneiden wir mit Ebenen durch die Zentren der
magenta Kugeln. Es entsteht ein abgeschrupptes Tetraeder.
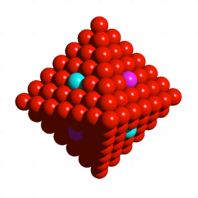
Tetraeder im Oktaeder
3.4
WŸrfel
3.4.1
WŸrfel als Kugelpackung
Wir zeigen schichtweise
den Aufbau des WŸrfels.
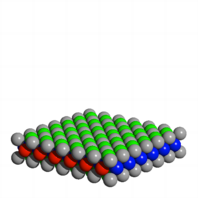
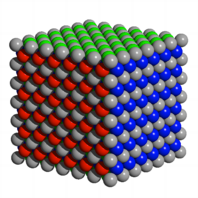
Aufbau des WŸrfel
Diese Anordnung der
Kugel wird als ãflŠchenzentriertÒ bezeichnet. Die grauen Kugeln bilden die
Knoten eines WŸrfelgitters, die weiteren Kugeln sitzen jeweils in den FlŠchenmitten.
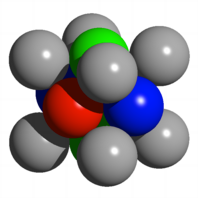
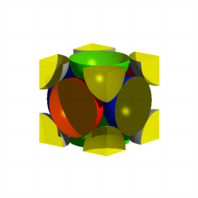
WŸrfelecken und
FlŠchenmitten
Der WŸrfel, dessen
Ecken die Mittelpunkte der grauen Kugeln sind, hat eine SeitenlŠnge 
und enthŠlt acht
Achtelkugeln und sechs Halbkugeln, insgesamt also vier Kugeln. FŸr den
AusnŸtzungsgrad erhalten wir:
3.4.2
Anzahl Kugeln
Bei der Berechnung der
Anzahl 
der Kugeln
orientieren wir uns an den Farben. FŸr die KantenlŠnge n haben wir zunŠchst 
graue Kugeln.
Dann gibt es zum Beispiel 
rote Kugeln und
eben so viele grŸne und blaue Kugeln. Somit haben wir:
3.4.3
Rhombendodekaeder
ZunŠchst der WŸrfel:
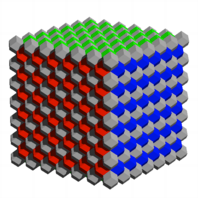
WŸrfel aus
Rhombendodekaeder
Das einzelne
Rhombendodekaeder ist nochmals in einer anderen Ausrichtung.
Ausrichtung des
Rhombendodekaeders
Die beiden folgenden
Abbildungen zeigen zunŠchst die unterste Schicht und dann darŸber gelagert die
zweitunterste Schicht.
Unterste und
zweitunterste Schicht.
Die dritte Schicht ist
dann wieder gleich wie die unterste Schicht.
3.4.4
Link mit dem Tetraeder
Wir markieren die
WŸrfelecken abwechslungsweise magenta und cyan. Es hat dann vier magenta und
vier cyan Kugeln. Die vier magenta Kugeln sind Ecken eines regelmŠ§igen
Tetraeders, ebenso natŸrlich die cyan blauen Kugeln. Nun zerschneiden wir mit
Ebenen durch die Zentren der magenta Kugeln. Es entsteht ein abgeschrupptes
Tetraeder.
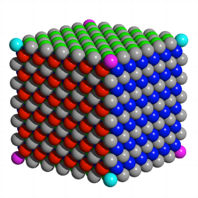
Linke mit dem Tetraeder
3.5
Sechskantprisma
3.5.1
Sechskantprisma als Kugelpackung
Prisma
Interessant ist, dass
die drei durch verschiedene Farben angedeuteten Schichten auch verschieden Form
haben. Dazu sehen wir uns die drei untersten Schichten von oben her an.
Unterste Schicht
Die unterste Schicht
ist ein regelmŠ§iges Sechseck.
Nun geben wir die
zweitunterste Schicht dazu sowie in einem weiteren Bild auch noch die
drittunterste Schicht.
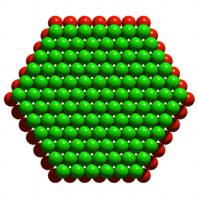
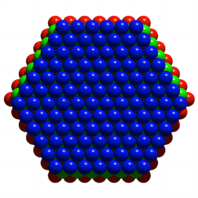
Die zwei und drei
untersten Schichten
Wir sehen, dass diese
beiden Schichten keine regelmŠ§igen Sechseck mehr sind. Die SeitenlŠngen
wechseln zwischen 6 und 5. Zudem ist die blaue Schicht gegenŸber der grŸnen
Schicht verdreht.
3.5.2
Anzahl Kugeln
Wir berechnen die
Anzahlen der Kugel schichtweise. Die unterste Schicht kšnnen wir in sechs
Sektoren zerlegen, wobei eine zentrale Kugel Ÿbrig bleibt.
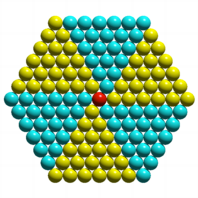
Unterste Schicht,
Zerlegung in Sektoren
FŸr die Anzahl 
der Kugeln gilt
daher:
Die zweitunterste
Schicht kann wie folgt zerlegt werden.
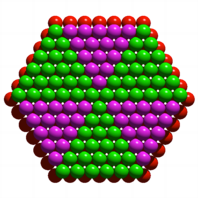
Zweitunterste Schicht
In der Mitte haben wir
keine Kugel, sondern ein Loch. Die Sektoren haben unterschiedliche Grš§e. Wir
finden:
Mit etwas Phantasie
hŠtten wir das auch ohne Rechnung sehen kšnnen. FŸr die drittunterste Schicht
gilt dieselbe Formel.
FŸr ein Prisma der Hšhe
h (gezŠhlt werden die roten Schichten)
erhalten wir:
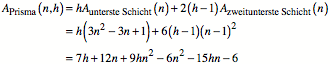
3.5.3
Rhombendodekaeder
Die Rhombendodekaeder
sind gleich ausgerichtet wie beim Tetraeder.
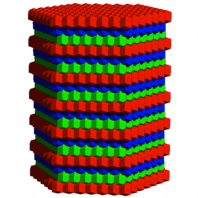
Rhombendodekaeder
Literatur
[Leppmeier 1997] Leppmeier, Max: Kugelpackungen von Kepler bis heute. Braunschweig: Vieweg 1997. ISBN 3-528-06792-6