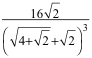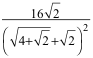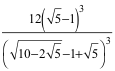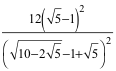Hans Walser, [20211218]

Kugeln in Kugel

Anregung: Mathe.Entdecker: Konstanz neu vermessen

1 Große und kleine Kugeln

Am Weihnachtsbaum hängen Kugeln in zwei Größen.

Die eine Frage: Wie oft passt das Volumen einer kleinen Kugel in das Volumen einer großen Kugel?

Die andere Frage: Wie oft passt eine kleine Kugel in eine große Kugel?

Beispiel: Die große Kugel habe den Radius R = 1. Die kleine Kugel habe den Radius r:

Das Volumen der kleinen Kugel passt sieben Mal in das Volumen der großen Kugel (nachrechnen).

Die kleine Kugel passt aber nur einmal in die große Kugel: der Durchmesser der kleinen Kugel ist größer als der Radius der großen Kugel. Selbst wenn die kleine Kugel die große Kugel von innen berührt, enthält sie den Mittelpunkt der großen Kugel im Innern. Eine gleich große zweite kleine Kugel enthielte ebenfalls diesen Mittelpunkt. Die beiden kleinen Kugeln müssten sich also überschneiden.

Erst für

fänden zwei (oder mehr) kleine Kugeln in der großen Kugel Platz.

2 Kugelpackung in der Kugel

Wir wollen n kongruente kleine Kugeln in die Einheitskugel (R = 1) platzieren.

Was ist der größtmögliche Radius r der kleinen Kugeln?

Wie müssen die kleinen Kugeln angeordnet werden?

Die Einheitskugel wird im Folgenden grün dargestellt, die kleinen Kugeln rot. Es werden jeweils auch der gesamte Volumenanteil und der gesamte Oberflächenanteil der n kleinen Kugeln im Vergleich zur Einheitskugel angegeben. Der gesamte Volumenanteil ist kleiner als 1. Der gesamte Oberflächenanteil divergiert mit wachsendem n.

3 Zwei kleine Kugeln

Für zwei eingepasste Kugeln erhalten wir den optimalen den Radius ½ (Abb. 1).

Der gesamte Volumenanteil der beiden roten Kugeln gegenüber der grünen Einheitskugel ist 1/4. Volumenmäßig hätten also noch sechs weitere rote Kugeln Platz.

Der gesamte Oberflächenanteil der beiden roten Kugeln ist halb so groß wie die Oberfläche der grünen Einheitskugel.

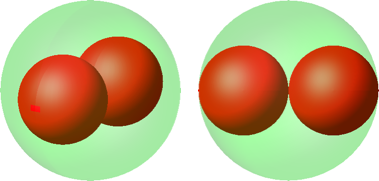
Abb. 1: Zwei Kugeln

4 Drei kleine Kugeln

Drei kleine Kugeln lassen sich so anordnen, dass ihre Mittelpunkte ein gleichseitiges Dreieck bilden (Abb. 2).

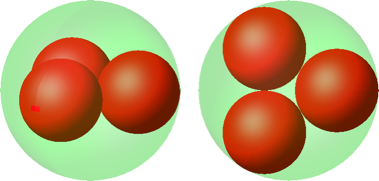
Abb. 2: Drei Kugeln

Daten:

Radius einer kleinen roten Kugel		0.4641
Volumenanteil		0.2999
Oberflächenanteil		0.6462

5 Vier kleine Kugeln

Wir untersuchen zwei verschiedene Anordnungen.

5.1 Quadratische Anordnung

Zunächst die quadratische Anordnung (Abb. 3).

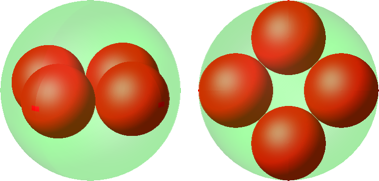
Abb. 3: Vier kleine Kugeln in quadratischer Anordnung

Daten:

Radius einer kleinen roten Kugel		0.4142
Volumenanteil		0.2843
Oberflächenanteil		0.6863

5.2 Tetraedrische Anordnung

Die vier Kugelzentren bilden die Ecken eines regelmäßigen Tetraeders (Abb. 4 und Abb. 5).

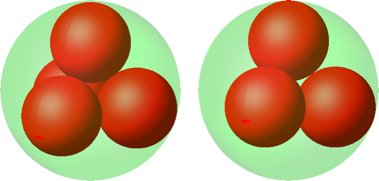
Abb. 4: Vier kleine Kugeln in tetraedrischer Anordnung

Daten:

Radius einer kleinen roten Kugel		0.4495
Volumenanteil		0.3633
Oberflächenanteil		0.8082

Die tetraedrische Lösung ist besser als die quadratische. Ich vermute, dass sie die optimale Lösung ist.

Die Abbildung 5 gibt eine andere Sicht der vier Kugeln in tetraedrischer Anordnung.

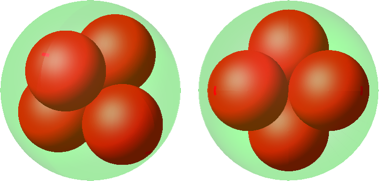
Abb. 5: Andere Sicht

5.3 Metamorphose

Die Abbildung 6 zeigt die Metamorphose der quadratischen Anordnung (Abb. 3) in die tetraedrische Anordnung (Abb. 5). Die Kugelradien wachsen sichtbar bei der Annäherung an die tetraedrische Anordnung. Wo ist im dritten Bild die vierte kleine Kugel?

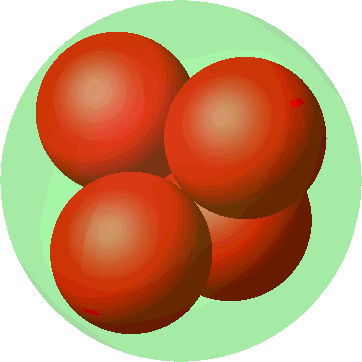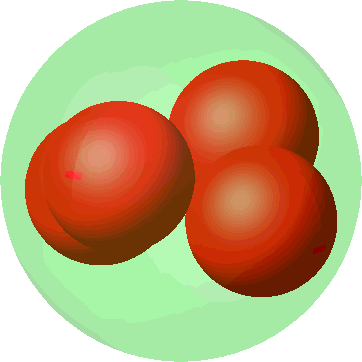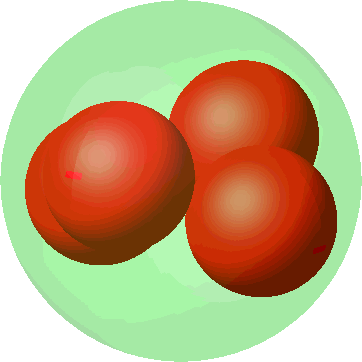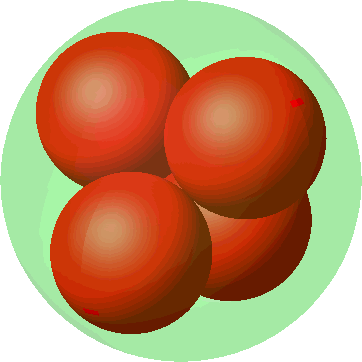
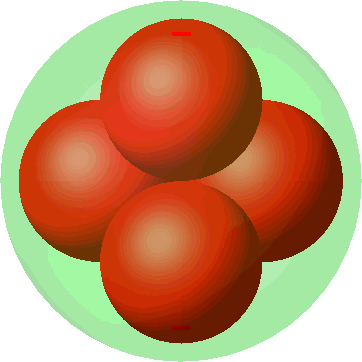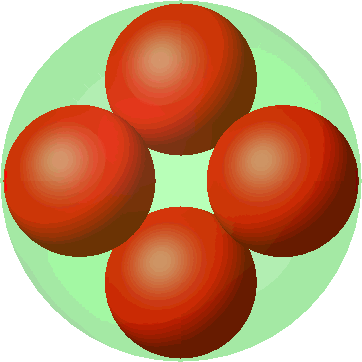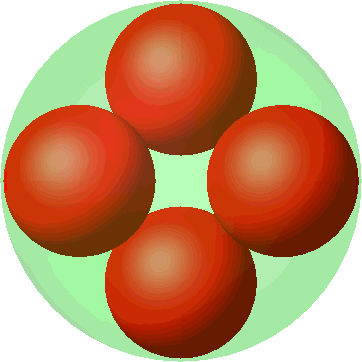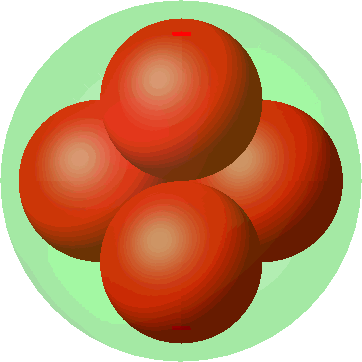
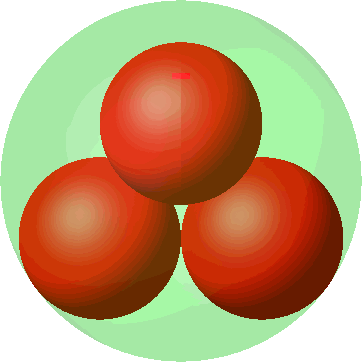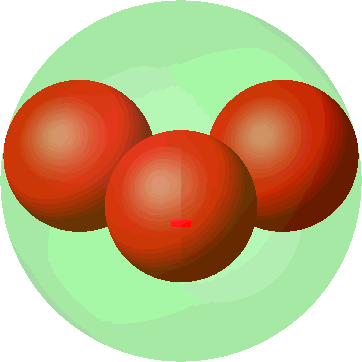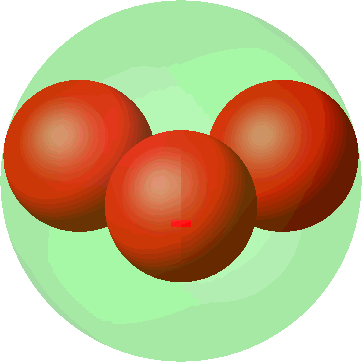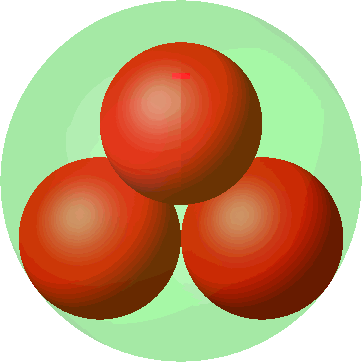
Abb. 6: Metamorphose

6 Fünf Kugeln

Die Abbildung 7 zeigt eine Lösung mit fünf Kugeln. Der Autor ist aber nicht so sicher, ob das eine optimale Lösung ist.

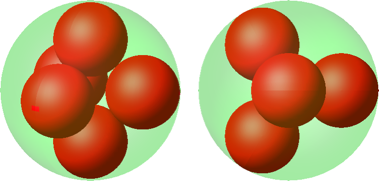
Abb. 7: Fünf Kugeln

Daten:

Radius einer kleinen roten Kugel		0.4142
Volumenanteil		0.3553
Oberflächenanteil		0.8579

7 Sechs kleine Kugeln

7.1 Oktaedrische Anordnung

Die Mittelpunkte der sechs kleinen Kugeln sind die Eckpunkte eines regelmäßigen Oktaeders (Abb. 8).

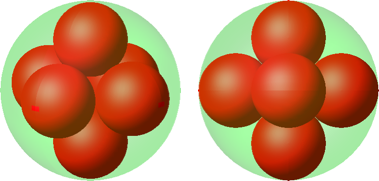
Abb. 8: Sechs Kugeln

Daten:

Radius einer kleinen roten Kugel		0.4142
Volumenanteil		0.4264
Oberflächenanteil		1.0294

Die Summe der Oberflächen der sechs roten Kugeln ist nun größer als die Oberfläche der grünen Einheitskugel.

Wird eine der sechs Kugeln entfernt, ergibt sich eine Lösung für fünf Kugeln.

Werden zwei diametrale Kugeln entfernt, bilden die restlichen vier Kugeln eine quadratische Anordnung (Abb. 3).

7.2 Antiprisma

Wir beginnen mit sechs kleinen Kugeln in ebener hexagonaler Anordnung (Abb. 9). Der Radius der kleinen Kugeln ist ein Drittel. Wir könnten in der Mitte noch eine siebte kleine Kugel einfügen.

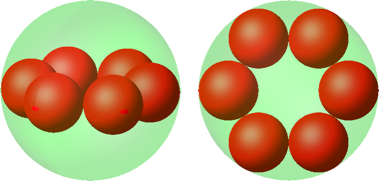
Abb. 9: Hexagonale Anordnung

Nun heben wir jede zweite Kugel an und schieben die drei Kugeln dazwischen um gleich viel hinunter. Die Radien vergrößern wir so, dass sich benachbarte Kugeln dauernd berühren. Dies machen wir bis zum Anschlag (Abb. 10).

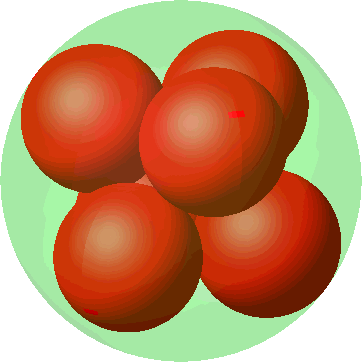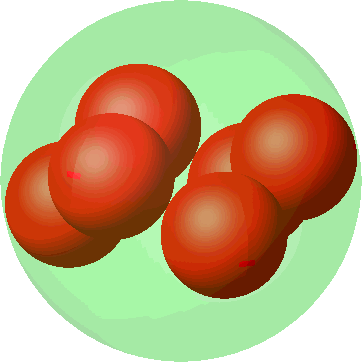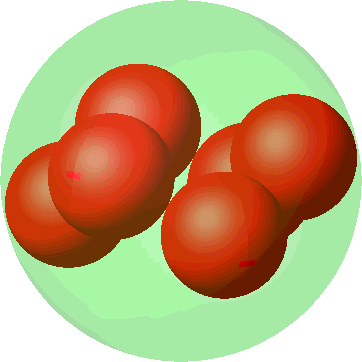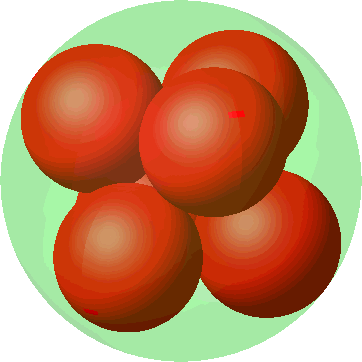
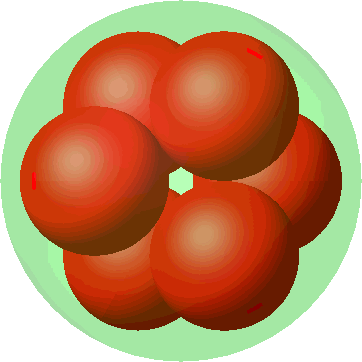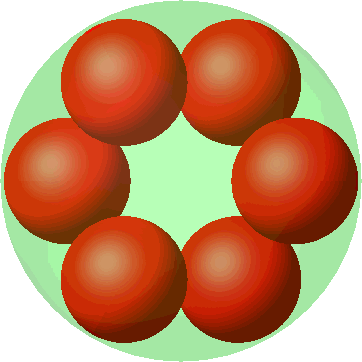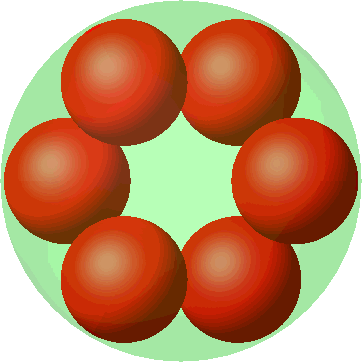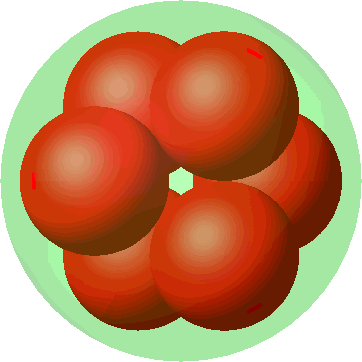
Abb. 10: Metamorphose

In der Endlage am Anschlag haben wir ein Antiprisma mit einem gleichseitigen Dreieck als Grundfläche (Abb. 11). Es ist wiederum das Oktaeder (Abb. 8), aber in einer anderen Sicht.

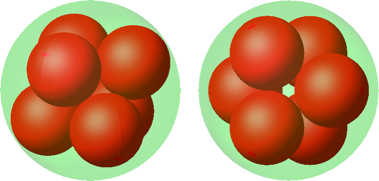
Abb. 11: Oktaeder als Antiprisma

Man kann jetzt darüber philosophieren, dass auch das Tetraeder (Abb. 4 und 5) ein Antiprisma ist, mit einer Strecke als „Grundfläche“. Das bringt den Dimensionsbegriff durcheinander.

8 Sieben kleine Kugeln

Frau Königin, Ihr seid die Schönste hier,

Aber Schneewittchen über den Bergen

Bei den sieben Zwergen

Ist noch tausendmal schöner als Ihr.

9 Acht kleine Kugeln

9.1 Würfel-Anordnung

Natürlich denkt man an die Anordnung in den acht Würfelecken (Abb. 12).

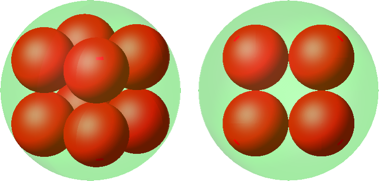
Abb. 12: Würfelecken

Daten:

Radius einer kleinen roten Kugel		0.3660
Volumenanteil		0.3923
Oberflächenanteil		1.0718

9.2 Antiprisma

Wie sieht es mit dem Antiprisma aus (Abb. 13)? Das Antiprisma hat eine quadratische Grundfläche.

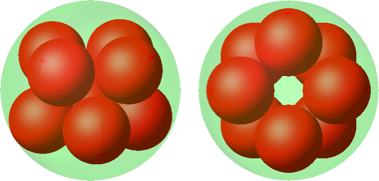
Abb. 13: Antiprisma

Daten:

Radius einer kleinen roten Kugel		0.3780
Volumenanteil		0.4322
Oberflächenanteil		1.1432

Die antiprismatische Lösung ist besser als die Lösung mit den Würfelecken. Der Autor vermutet, dass dies die optimale Lösung ist.

Die Abbildung 14 gibt die Genesis des Antiprismas aus einer ebenen oktogonalen Anordnung.

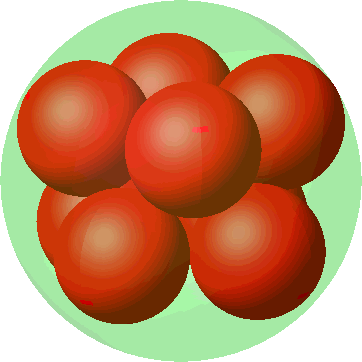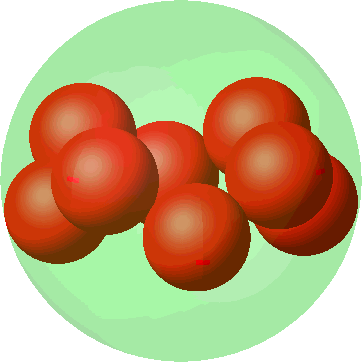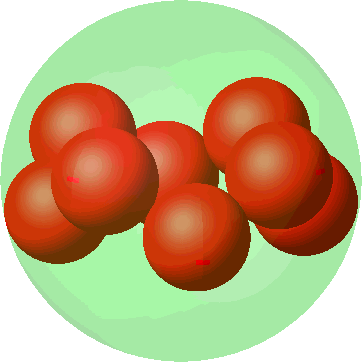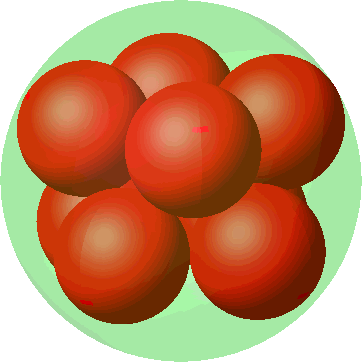
Abb. 14: Genesis des Antiprisma

10 Sieben kleine rote Kugeln

Wenn wir beim Antiprisma (Abb. 13) eine Kugel entfernen, bleibt die vermutlich optimale Lösung für sieben kleine rote Kugeln übrig. Weder schön noch symmetrisch.

11 Zwischenpause

Es scheint keine systematische Lösung für alle natürlichen Zahlen n zu geben. Jeder Fall ist für sich spannend.

12 Zwölf Kugeln

12.1 Ikosaedrische Anordnung

Die zwölf Kugelzentren liegen in den Ecken eines Ikosaeders (Abb. 15).

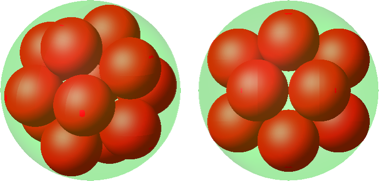
Abb. 15: Ikosaedrische Anordnung

Daten:

Radius einer kleinen roten Kugel		0.3446
Volumenanteil		0.4910
Oberflächenanteil		1.4248

Der Volumenanteil ist fast die Hälfte.

12.2 Kuboktaedrische Anordnung

Die zwölf Kugelzentren liegen in den Ecken eines Kuboktaeders (Abb. 16). Man kann es auch so sagen: die zwölf Kugelzentren liegen in den Kantenmitten eines Würfels.

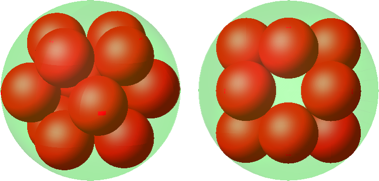
Abb. 16: Zwölf Kugeln

Wir erhalten rationale Daten:

Radius einer kleinen roten Kugel
Volumenanteil
Oberflächenanteil

Die Summe der Oberflächen der zwölf roten Kugeln ist größer als die Oberfläche der grünen Einheitskugel.

13 Dreizehn kleine rote Kugeln

Wir können in die Mitte der Konfiguration der Abbildung 16 noch eine dreizehnte gleich große Kugel platzieren (blau in Abb. 17). Dass diese blaue Kugel größer zu sein scheint als die roten, ist eine optische Täuschung.

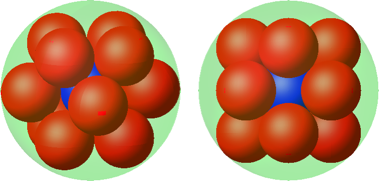
Abb. 17: Tredecim

Wir erhalten rationale Daten:

Radius einer kleinen Kugel		0.3333
Volumenanteil		0.4815
Oberflächenanteil		1.4444

Die Konfiguration mit den dreizehn Kugeln ist ein Ausschnitt aus der dichtesten (globalen) Kugelpackung (Vermutung 1611 von Johannes Kepler, Beweis 1998 Thomas Hales). Dass diese Packung trotzdem schlechter ist als die ikosaedrische Packung (Abb. 15), ist kein Widerspruch. Es hängt damit zusammen, dass wir mit lokalen endlichen Packungen arbeiten.

Weblinks

Mathe.Entdecker: Konstanz neu vermessen

https://mathcitymap.eu/de/konstanz-neu-vermessen/

Kleine Kugel, große Kugel

https://mathcitymap.eu/de/portal/#!/trail/492255/task/6810662