Hans Walser, [20160724]
Kugelumriss im SchrŠgbild
1 Worum geht es?
Der Umriss einer im SchrŠgbild dargestellten Kugel ist eine Ellipse. Es wird ein Rezept zur schnellen Konstruktion vorgestellt.
2 Die Sonne bringt es an den Tag
Das Schattenbild einer Kugel bei schrŠg einfallendem Licht (Sonnenlicht, praktisch Parallelbeleuchtung) ist eine Ellipse (Abb. 1).

Abb. 1: SchrŠgbild der Kugel
Allgemein ist der Umriss eines SchrŠgbildes (Kavalierperspektive, japanische Axonometrie, MilitŠrperspektive) einer Kugel eine Ellipse.
3 Inkugel eines Wźrfels
Zu einem Wźrfel im SchrŠgbild (Abb. 2) zeichnen wir die Inkugel.
Das SchrŠgbild ist an sich eine schematische Zeichnung und unanschaulich. Es ist nicht mšglich, einen richtigen Wźrfel auch nur nŠherungsweise so wie im SchrŠgbild zu sehen. Der Wźrfel existiert nur in unserem Vorstellungsraum.
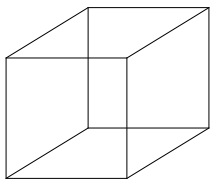
Abb. 2: SchrŠgbild des Wźrfels
Die Mittelpunkte der Vorderfront und der Rźckwand sind die Brennpunkte der Kugelumrissellipse (Abb. 3). In unserem Vorstellungsraum verlŠuft die Inkugel durch diese beiden Punkte.
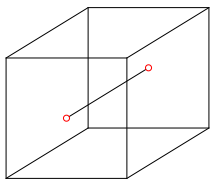
Abb. 3: Brennpunkte
Um den Mittelpunkt zeichnen wir einen Kreis, dessen Durchmesser gleich gro§ ist wie die KantenlŠnge des Wźrfels (Abb. 4). In unserem geografischen Vorstellungsraum ist dieser Kreis der 90ˇE / 90ˇW –Meridiankreis.
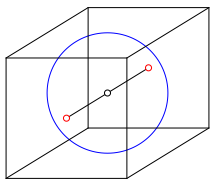
Abb. 4: Kreis
Den Kreis der Abbildung 4 schneiden wir mit der Mittelsenkrechten der beiden Brennpunkte (Abb. 5). Dieser Schritt ist rein planimetrisch ohne Bezug zum Vorstellungsraum (oder vielleicht doch?).
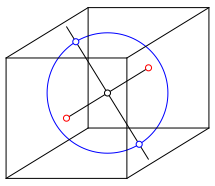
Abb. 5: Mittelsenkrechte
Der so erhaltene Durchmesser des Kreises ist die kurze Achse der gesuchten Umrissellipse. Zusammen mit den Brennpunkten haben wir jetzt genźgend Information, um die Ellipse zu zeichnen (Abb. 6).
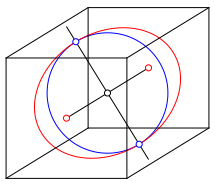
Abb. 6: Umrissellipse der Inkugel
In der Abbildung 7 sind zusŠtzlich die Bilder des €quators und des Greenwich-Gro§kreises unseres Vorstellungsraumes eingetragen, ebenso die Bilder von Nord- und Sźdpol. Dazu wurde mit konjugierten Durchmessern gearbeitet.
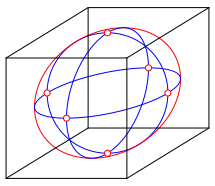
Abb. 7: Bis hin zu den Polen
Die Figur sieht unnatźrlich gequetscht aus. Das ist so bei SchrŠgbildern.
4 Einheitskugel im Koordinatensystem-SchrŠgbild
Wir zeichnen den Umriss der Einheitskugel in einem Koordinatensystem-SchrŠgbild (Abb. 8). Auf jeder Achse ist der Einheitspunkt eingezeichnet.

Abb. 8: Koordinatensystem
Wir spiegeln die Einheitspunkte am Ursprung (Abb. 9). Auf der x-Achse erhalten wir so die Brennpunkte der gesuchten Umrissellipse.
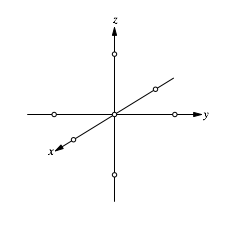
Abb. 9: Spiegeln der Einheitspunkte. Brennpunkte
Durch die Einheitspunkte auf der y- und z-Achse zeichnen wir einen Kreis und schneiden diesen mit der Mittelsenkrechten der beiden Brennpunkte (Abb. 10). So erhalten wir die kurze Achse der gesuchten Umrissellipse.
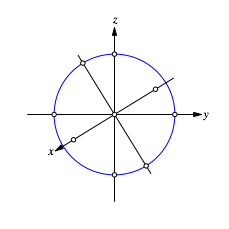
Abb. 10: Kurze Achse
Nun kšnnen wir die Umrissellipse zeichnen (Abb. 11).
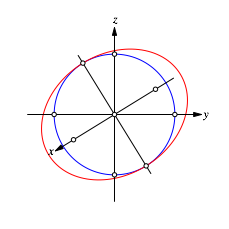
Abb. 11: Umrissellipse
In der Abbildung 12 sind zusŠtzlich die Bilder der Einheitskreise in der x,y-Ebene und der x,z-Ebene eingezeichnet.
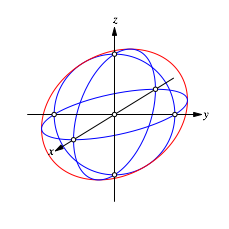
Abb. 12: Bilder der Einheitskreise in den Rissebenen