Hans Walser, [20140202]
Kurven im Viereck
1 Unterteilung der Viereckseiten
Wir unterteilen die Seiten eines grźnen Vierecks im gleichen VerhŠltnis. Dies kann auf zwei Arten geschehen.
Die Abbildung 1 zeigt eine ăgegengleicheŇ Unterteilung. Die vier Teilpunkte bilden ein diagonalenparalleles blaues Parallelogramm.
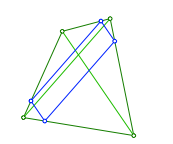
Abb. 1: Gegengleiche Unterteilung
Die Abbildung 2 zeigt eine gleichorientierte Unterteilung. Die vier Teilpunkte bilden ein unregelmŠ§iges blaues Viereck.
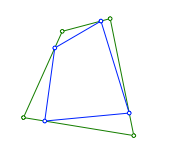
Abb. 2: Gleichsinnige Unterteilung
2 Gegengleiche Unterteilung
Der Ort der Mittelpunkte der blauen Parallelogramme (Abb. 1) ist eine Gerade durch die Mittelpunkte der beiden Diagonalen des grźnen Viereckes (Abb. 3).
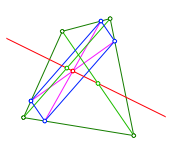
Abb. 3: Ort der Mittelpunkte
Nachweis rechnerisch.
Es seien 
die
Ortsvektoren der Ecken des grźnen Viereckes. Fźr die Eckpunkte des blauen
Parallelgramms gilt dann der Reihe nach:
Fźr den Mittelpunkt des blauen Parallelogramms genźgt es, den Mittelpunkt zweier gegenźberliegender Ecken zu nehmen, also:
Das ist eine
Geradengleichung. Die Gerade verlŠuft fźr 
beziehungsweise fźr 
durch je
einen Diagonalen-Mittelpunkt. Fźr 
erhalten
wir den Eckenschwerpunkt des grźnen Viereckes.
3 Gleichsinnige Unterteilung
Dieser Fall ist spannender. Beim grźnen Viereck kšnnen wir nicht mehr von einem ăMittelpunktŇ reden sondern mźssen prŠzisieren.
3.1 Eckenschwerpunkte
Der Ort der Eckenschwerpunkte der blauen Vierecke ist ein fester Punkt, nŠmlich der Eckenschwerpunkt des grźnen Viereckes.
Nachweis wiederum rechnerisch. Fźr die Ecken des blauen Viereckes gilt der Reihe nach:
Fźr den Eckenschwerpunkt erhalten wir daraus:
3.2 Diagonalen-Schnittpunkte
Die Abbildung 4 zeigt den Ort der Diagonalen-Schnittpunkte der blauen Vierecke.
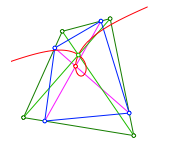
Abb. 4: Ort der Diagonalen-Schnittpunkte
Wir erhalten eine Kurve die ich nicht kenne. Sie hat im Diagonalen-Schnittpunkt des grźnen Viereckes einen Doppelpunkt. Auch scheint sie an beiden Enden sich derselben Geraden asymtotisch anzunŠhern.