Hans Walser, [20150117]
k-nomialkurven
1 Worum geht es?
Die Polynome, welche zu den Bi-, Tri, ... , k-nomialkoeffizienten fŸhren, werden als Funktionsterme gedeutet und die zugehšrigen Grafen geplottet.
Die k-nomialkoeffizienten ergeben sich als Koeffizienten von:
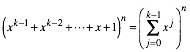
Die k-nomialkurven sind die Funktionsgrafen von.
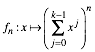
2 Binomialkurven
Die
Binomialkoeffizienten kšnnen als Koeffizienten von 
generiert
werden:
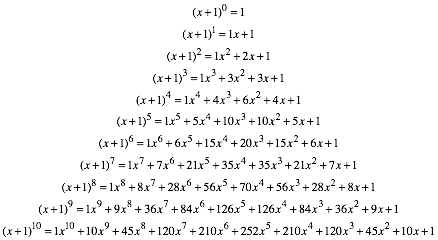
Die
Abbildung 1 zeigt nun die Grafen der Funktionen 
fŸr 
. FŸr gerade n
sind die Kurven rot, fŸr ungerade n
blau gezeichnet.
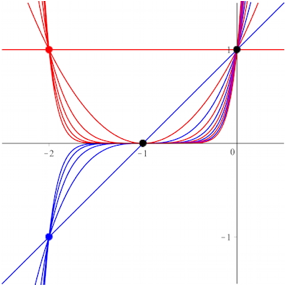
Abb. 1: Binomialkurven
3 Trinomialkurven
Die
Binomialkoeffizienten kšnnen als Koeffizienten von 
generiert
werden:
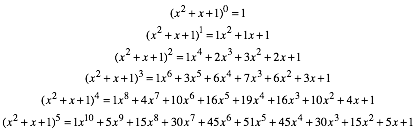
Die Rekursion ist offensichtlich. Jede Zahl ist die Summe der drei nŠchstgelegenen Zahlen in der oberen Reihe.
Die
Abbildung 2 zeigt nun die Grafen der Funktionen 
fŸr 
. FŸr gerade n
sind die Kurven rot, fŸr ungerade n
blau gezeichnet.
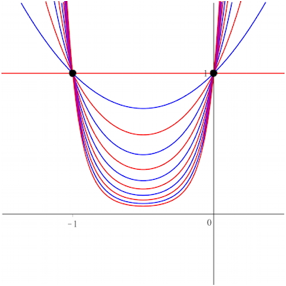
Abb. 2: Trinomialkurven
4 Tetranomialkurven
(Ich frage mich, ob die griechischen Zahlwšrter hier angebracht sind.)
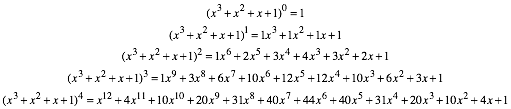
Jede Zahl ist die Summe der vier nŠchstgelegenen Zahlen in der oberen Reihe.
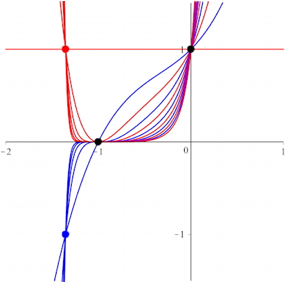
Abb. 3: Tetranomialkurven
Der rote und der blaue Punkt links haben die x-Koordinate (CAS):
5 Pentanomialkurven
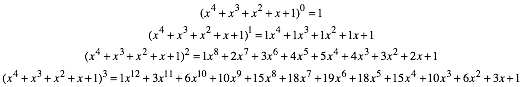
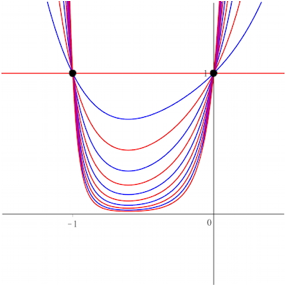
Abb. 4: Pentanomialkurven
6 Hexanomialkurven
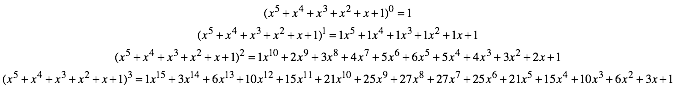
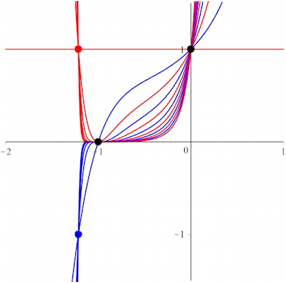
Abb. 5: Hexanomialkurven
Der rote
und der blaue Punkt links haben die x-Koordinate
(CAS) 
.
7 Heptanomialkurven
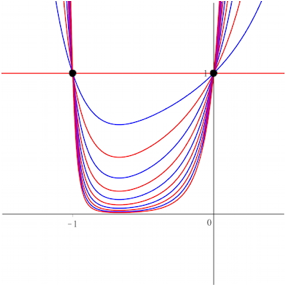
Abb. 6: Heptanomialkurven
8 Oktanomialkurven
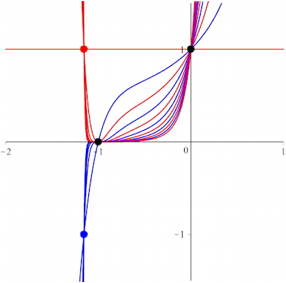
Abb. 7: Oktanomialkurven
9 ParitŠtsunterschiede
FŸr ungerades k verlaufen die Kurven oberhalb der x-Achse und durch die beiden Punkte (0, 1) und (–1, 1).
Die Abbildung 8 zeigt die Situation fŸr k = 49.
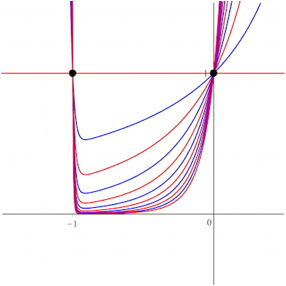
Abb. 8: k = 49
FŸr gerades k ist die Sache spannender. Alle Kurven verlaufen durch (0, 1), und bis auf die Kurve fŸr n = 0 durch (–1, 0). Dir Kurven fŸr gerades n verlaufen durch einen Punkt mit einer x-Koordinate < –1 und der y-Koordinate 1, fŸr ungerades n ist die y-Koordinate –1.
Die Abbildung 9 zeigt die Situation fŸr k = 50.
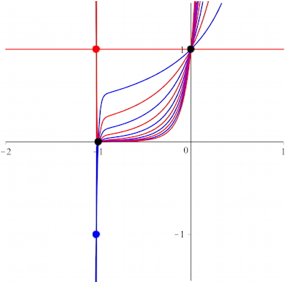
Abb. 9: k = 50
Der rote
und der blaue Punkt haben die x-Koordinate:
.
Diese x-Koordinaten finden sich als Lšsung der Gleichung:
Die Tabelle 1 gibt die Lšsungen (CAS) fŸr k = 2, 4, ... , 50.
|
k |
x-Koordinate |
|
2 |
–2 |
|
4 |
–1.353209965 |
|
6 |
–1.214862322 |
|
8 |
–1.154423057 |
|
10 |
–1.120528255 |
|
12 |
–1.098836878 |
|
14 |
–1.083763094 |
|
16 |
–1.072679116 |
|
18 |
–1.064185914 |
|
20 |
–1.057470136 |
|
22 |
–1.052026651 |
|
24 |
–1.047525179 |
|
26 |
–1.043740659 |
|
28 |
–1.040514435 |
|
30 |
–1.037731451 |
|
32 |
–1.035306233 |
|
34 |
–1.033173957 |
|
36 |
–1.031284569 |
|
38 |
–1.029598804 |
|
40 |
–1.028085427 |
|
42 |
–1.026719281 |
|
44 |
–1.025479877 |
|
46 |
–1.024350359 |
|
48 |
–1.023316734 |
|
50 |
–1.022367287 |
Tab. 1: x-Koordinaten