Hans Walser, [20101114a]

Der Satz von Lehmann-Rosenbaum

Anregung: I. L., B.

1 Worum geht es?

Zu gegebenem unterteilen wir die Seiten eines Dreiecks mit den Teilpunkten und :

Weiter sei der Schnittpunkt der beiden Ecktransversalen und . Die Abbildung zeigt die Situation für . Schließlich sei der Schwerpunkt des Dreiecks .

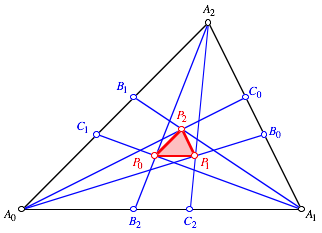
Situation

Dann gilt der Satz von Lehmann-Rosenbaum: Die zentrische Streckung mit dem Zentrum S und dem Faktor bildet das Dreieck auf das Dreieck ab:

2 Beweis

Wir beweisen den Satz zunächst für rationales .

2.1 Rationales Teilverhältnis

Den Beweis verdanke ich Felix, MSG-Schüler der Klasse 12, Berlin.

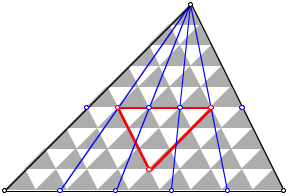
Es sei mit , und . Wir rastern das Dreieck in kanonischer Weise kongruente Teildreiecke. Die Abbildungen zeigen die Fälle und der Reihe nach , also .

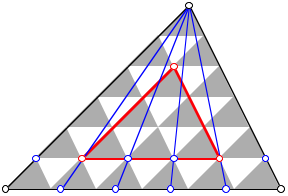
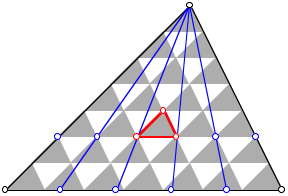
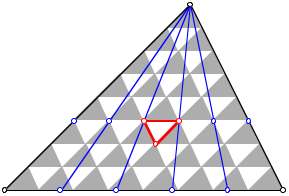
Im Sinne eines proof without words sehen wir für den Streckfaktor f:

Schließlich ist:

2.2 Reelles Teilverhältnis

Für arbeiten wir mit dem dedekindschen Schnitt.

3 Ergänzungen

3.1 Weitere Teilverhältnisse

Die folgenden Teilverhältnisse lassen sich ebenfalls aus der Rasterung ablesen:

Der Punkt teilt die beiden Ecktransversalen und so dass:

Der Punkt teilt die Schwerlinie so dass:

3.2 Ecktransversalen außerhalb des Dreieckes

Der Satz gilt für beliebige . Interessant sind die Sonderfälle der Funktion:

Für hat die Funktion einen Pol. Die beiden Ecktransversalen und werden parallel. Für ist ; das Dreieck hat das Ausgangsdreieck als Seitenmittendreieck.

3.3 Komplementarität

Für und erhalten wir Ecktransversalen, die sich decken. Die Abbildung zeigt die Situation für und .

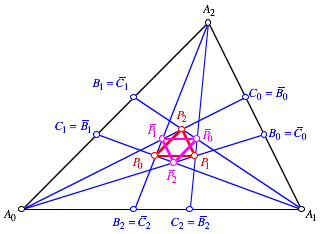
Komplementarität

Wegen

und

folgt:

Den Streckfaktor können wir vereinfachen: