Hans Walser, [20150711]
Lehrerdreieck
1 Worum geht es?
Das Folgende ist nicht ernst zu nehmen.
2 Der KŠfer
Ein KŠfer marschiert drei LŠngeneinheiten geradeaus und hinterlŠsst eine rote Farbspur. Dann Šndert er den Farboutput auf grŸn und marschiert vier LŠngeneinheiten geradeaus. Beim €ndern des Farboutputs hat er mšglicherweise die Richtung geŠndert. Dann Šndert er auf blau und marschiert wieder geradeaus. Nach fŸnf LŠngeneinheiten kommt er zum Ausgangspunkt zurŸck.
3 Das Lehrerdreieck
In der Schule haben wir gelernt, dass ein Dreieck mit den SeitenlŠngen 3, 4 und 5 aussieht gemŠ§ Abbildung 1.
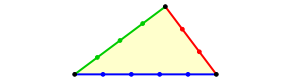
Abb. 1: Das Lehrerdreieck
Man erinnert sich an den Pythagoras. Die blaue FlŠche ist inhaltsgleich zur roten und grŸnen FlŠche zusammen. Man pflegt zu sagen, dass das Dreieck einen rechten Winkel habe (Abb. 2).
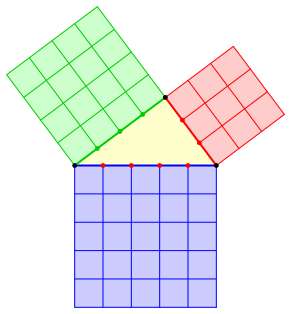
Abb. 2: Pythagoras
4 Der UhrenkŠfer
Nun ist es aber so, dass der KŠfer auf einer Uhr lebt (Abb. 3a).
Abb. 3: KŠferwelt. KŠferdreieck
Die Abbildung 3b zeigt sein Dreieck.
5 Pythagoras
Die Abbildung 4 zeigt eine Figur mit flŠchengleichen angesetzten Kreisvierecken. Die blaue FlŠche ist inhaltsgleich zur roten und grŸnen FlŠche zusammen.
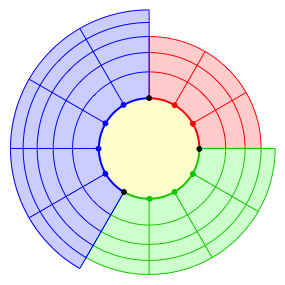
Abb. 4: Pythagoras
Die Abbildung 5 zeigt einen Versuch mit Quadraten. Die FlŠchengleichheit ist jetzt allerdings nicht mehr vorhanden.
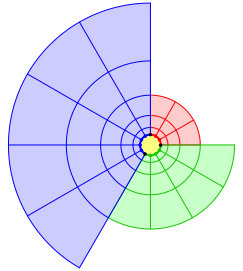
Abb. 5: Versuch mit Quadraten
Wir kšnnen die Quadrate auch nach innen ansetzen (Abb. 6).
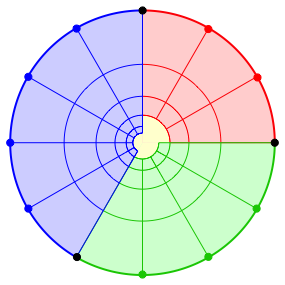
Abb. 6: Quadrate nach innen
6 Winkel im Sehnendreieck
Das Lehrerdreieck hat in der Ÿblichen Bezeichnung folgende Winkel:
Die beiden spitzen Winkel sind ãhŠsslichÒ.
Sir zeichnen nun im KŠferdreieck (Abb. 3b) das Sehnendreieck ein. Dieses hat die in der Abbildung 7 angegebenen ãschšnenÒ Winkel, allerdings keinen rechten Winkel.
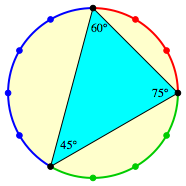
Abb. 7: Winkel im Sehnendreieck
7 Variante
Es geht auch auf einer Sechser-Uhr (Abb. 8).
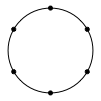
Abb. 8: Sechser-Uhr
Die Abbildung 9 zeigt das schrittweise Vorgehen.
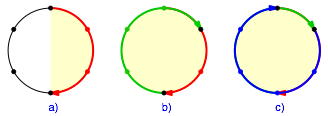
Abb. 9: Schrittweises Vorgehen
Der Kreis
wir zweimal durchfahren, da 
.
Die Abbildung 10 zeigt das zugehšrige Sehnendreieck.
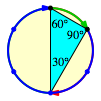
Abb. 10: Sehnendreieck
Es hat in
der Ÿblichen Notation die Winkel 
, 
und 
.