Hans Walser, [20160910]

Lemniskate

1 Worum geht es

Es werden Konstruktionen der Lemniskate mit Hilfe von Ellipsen und deren Brennpunkten besprochen.

2 Das Vorgehen

Wir zeichnen den Einheitskreis mit Mittelpunkt O(0, 0) und die Punkte S(1, 0),
N(–1, 0), E(0, 1), W(0, –1) (Abb. 1). Auf dem Einheitskreis wählen wir einen beliebigen Punkt P.

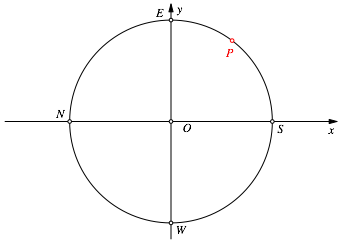
Abb. 1: Ein Punkt P auf dem Einheitskreis

Nun zeichnen wir die Ellipse mit den konjugierten Halbmessern OS und OP sowie deren Brennpunkte F₁ und F₂ (Abb. 2).

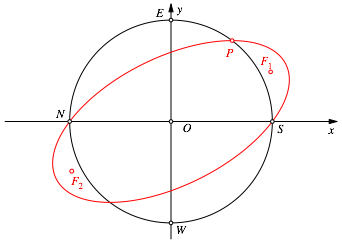
Abb. 2: Ellipse mit Brennpunkten

Die beiden Brennpunkte liegen auf der zu den Punkten S und N gehörenden Lemniskate (Abb. 3).

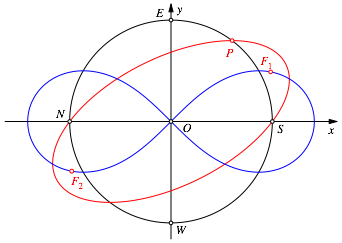
Abb. 3: Brennpunkte auf Lemniskate

Durch Variation von P erhalten wir so alle Punkte der Lemniskate (Ortslinie).

3 Lemniskate

Einige Fakten zur Lemniskate (Abb. 4).

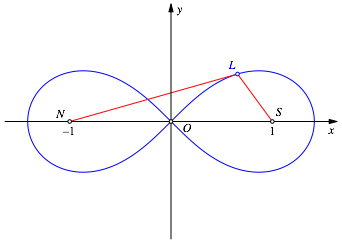
Abb. 4: Lemniskate

Für einen Punkt L auf der Lemniskate gilt (definierende Eigenschaft):

(1)

In Polarkoordinaten hat die Lemniskate die Gleichung:

(2)

In kartesischen Koordinaten hat die Lemniskate die Gleichung:

(3)

4 Beweis der Brennpunkteigenschaft

Der Punkt P (Abb. 2) habe die Koordinaten:

(4)

Der Faktor 2 beim Parameter t ist aus technischen Gründen dabei. Er vereinfacht die Formeln.

Da die beiden konjugierten Halbmesser OS und OP die gleiche Länge haben, sind die Hauptachsenrichtungen der Ellipse die Winkelhalbierenden der Halbmesser. Die Halbachsen a und b haben die Länge:

(5)

Daraus erhalten wir die halbe Brennpunktweite c:

(6)

Vergleich mit (2) beweist die Behauptung.

5 Umriss

Die Hüllkurve der sich durch die Variation von P ergebenden Ellipsenschar (rote Ellipse in Abb. 2 und 3) ist ihrerseits eine Ellipse (Abb. 5).

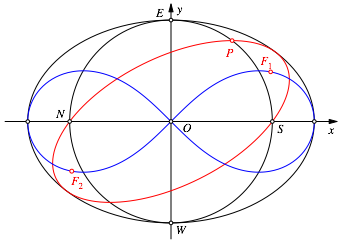
Abb. 5: Umrissellipse

Sie hat die Punkte N und S als Brennpunkte und verläuft durch die Punkt E und W.

Die lange Halbachse ist , die kurze Halbachse ist 1.

Wir können das durch eine kartografische Überlegung einsehen.

6 Schrägbild der Erdkugel

Wir stellen die Erdkugel auf den Tisch (Projektionsebene) und beleuchten von recht oben unter einem Winkel von 45° (Abb. 6a, Aufriss).

In der Projektionsebene erhalten wir so ein Schrägbild der Erdkugel (Abb. 6b, Grundriss).

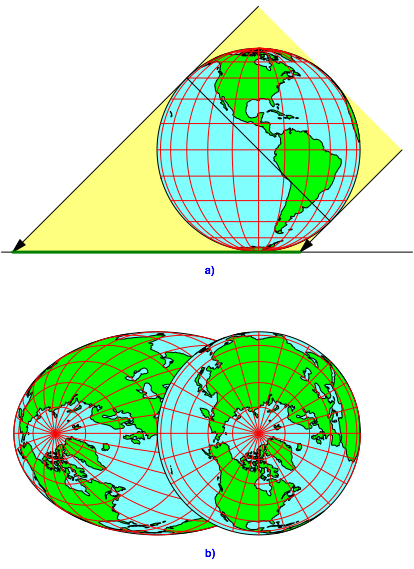
Abb. 6: Schrägbild der Erdkugel

Die Abbildung 7 zeigt das Schrägbild allein.

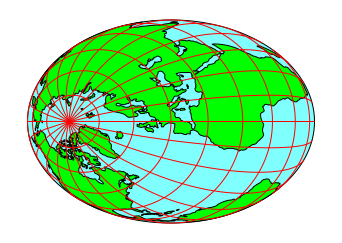
Abb. 7: Wo ist das schöne Tirol?

Die Breitenkreise sind in diesem Schrägbild als Kreise dargestellt. Der Äquator erscheint als Einheitskreis in der Mitte. Der Kartenumriss ist eine Ellipse mit der langen Halbachse und der kurzen Halbachse 1 (Schrägschnitt des sich durch die Projektionsstrahlen ergebenden Umrisszylinders). Die Brennpunkte dieser Ellipse sind die Bilder der beiden Pole (Überlegung mit Kugeln von Dandelin). Die Meridiane erscheinen als Ellipsen durch die beiden Pole, welche die Umrissellipse von innen berühren.

Die Abbildung 8 zeigt das Netz (15°-Maschenweite) der Meridiane und Breitenkreise ohne die Erde. Wegen der Projektionsrichtung 45° und der Maschenweite 15° berühren sich die Bilder der Breitenkreise.

Abb. 8: Meridiane und Breitenkreise

Die Figur der Abbildung 8 passt genau auf die Figur der Abbildung 5. Die rote Ellipse in der Abbildung 5 entspricht einem Meridianbild im Schrägbild.

Somit erhalten wir eine Variante der Lemniskaten-Konstruktion.

7 Variante der Lemniskaten-Konstruktion

Wir zeichnen die Punkte S(1, 0), N(–1, 0), E(0, 1), W(0, –1) und dazu die Ellipse mit den Brennpunkten S und N durch E. Auf der Ellipse wählen wir einen beliebigen Punkt Q (Abb. 9).

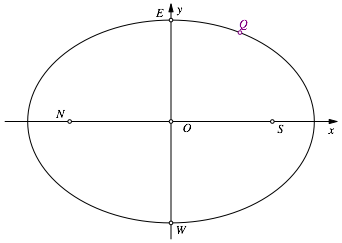
Abb. 9: Start mit Ellipse

Nun zeichnen wir eine zweite Ellipse mit dem Mittelpunkt O durch S, welche die erste Ellipse in Q berührt (Abb. 10). Ebenso zeichnen wir die Brennpunkte G₁ und G₂ dieser Ellipse.

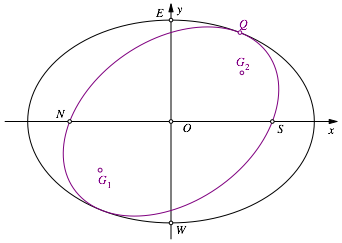
Abb. 10: Berührende Inellipse

Die Brennpunkte G₁ und G₂ liegen auf unserer Lemniskate (Abb. 11).

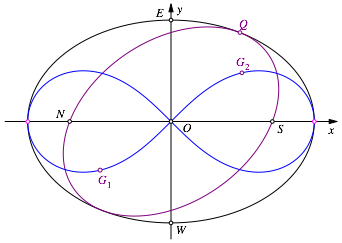
Abb. 11: Brennpunkte auf Lemniskate

Websites

Kartenprojektionen (04.09.2016):

http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html

Wikipedia, Lemniskate (08.09.2016):

https://de.wikipedia.org/wiki/Lemniskate_von_Bernoulli