Hans Walser, [20170929]

Lemniskate

1     Worum geht es?

Es wird eine Verallgemeinerung der Lemniskate von Bernoulli gezeigt.

2     Die Lemniskate von Bernoulli

Zu den beiden Punkten  und  zeichnen wir die Punkte  fźr welche das Produkt der AbstŠnde zu E0 und E1 konstant 1 ist. Es gilt also die implizite Gleichung:

 

                                                                                     (1)

 

 

Die entstehende Kurve (Abb. 1) ist die Lemniskate von Bernoulli (Jakob Bernoulli, 1654jul./1655greg-1705). Siehe Haftendorn (2017), S. 108f.

Abb. 1: Lemniskate von Bernoulli

3     Polardarstellung

Die Lemniskate hat in Polarkoordinaten die Darstellung:

 

                                                                                           (2)

 

 

Beweis:

Die Gleichung (1) schreiben wir in der Form:

 

                                                                                     (3)

 

 

Dies kann umgeformt werden zu:

 

                                                                                                 (4)

 

 

Die Gleichung (2) schreiben wir in der Form:

 

                                                                           (5)

 

 

Es ist:

 

                                                       (6)

 

 

Einsetzen in (5) liefert:

 

                                                                                           (7)

 

 

Daraus ergibt sich unmittelbar die Gleichung (4).

Die Polardarstellung (2) hat eine Tźcke: sie ist nicht fźr den ganzen Definitionsbereich  reell definiert, sondern nur fźr . Dazwischen ergeben sich imaginŠre Werte.

Wir kšnnen das Problem umgehen mit:

 

                                                                                         (8)

 

 

Die Abbildung 2 zeigt die zugehšrige Kurve.

 

           

Abb. 2: Absolutes Kleeblatt

4     Verallgemeinerung

In den Polardarstellungen (2) beziehungsweise (8) kommen je zweimal der Faktor 2 vor. Wir ersetzen diesen Faktor durch den positiven rationalen Faktor  und den Definitionsbereich durch . Wir arbeiten also mit den Polardarstellungen:

 

                                                                                       (9)

 

 

und:

 

                                                                                     (10)

 

 

Im Folgenden einige Beispiele. Es sind jeweils die Versionen ohne Betragsstriche beziehungsweise mit Betragsstrichen angegeben.

Die Kurven sind – mit Ausnahme der Lemniskate von Bernoulli – nicht identisch mit den Verallgemeinerungen unter [2].

4.1    p/q = 3

Abb. 3: p/q = 3

4.2    p/q = 4

Abb. 4: p/q = 4

4.3    p/q = 4/5

Abb. 5: p/q = 4/5

4.4    p/q = 5/4

Abb. 6: p/q = 5/4

Die beiden Figuren unterscheiden sich nicht.

4.5    p/q = 1/2

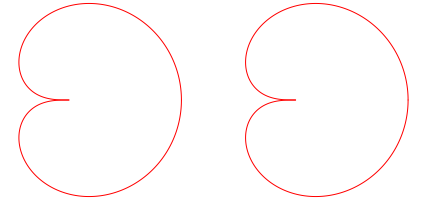
Abb. 7: p/q = 1/2

Die beiden Figuren unterscheiden sich nicht.

Es handelt sich nicht um die Kardioide.

 

Literatur

Haftendorn, Dšrte (2017): Kurven erkunden und verstehen. Mit GeoGebra und anderen Werkzeugen. Wiesbaden: Springer Spektrum. ISBN 978-3-658-14748-8.

 

Websites

[1] Hans Walser: Lemniskate (abgerufen 29.09.2017):

www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate/Lemniskate.htm

 

[2] Hans Walser: Lemniskate (abgerufen 29.09.2017):

www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate2/Lemniskate2.htm