Hans Walser, [20200221]
Lemniskate als Enveloppe von Kreisen
Anregung: Luchli 2020
1 Worum geht es?
Die BernoulliÕsche Lemniskate kann als Enveloppe von Kreisen erhalten werden. Hintergrund ist ein ebener Schnitt durch den Torus. Die Schnittebene ist tangential an einen Punkt des Kehlkreises des Torus.
2 Torus
Wir arbeiten mit einem Torus mit dem ãgro§enÒ Radius R (das ist der Radius vom Torusmittelpunkt zu den Zentren der Meridiankreise) und dem ãkleinenÒ Radius r (der Radius der Meridiankreise). Als Torusmittelpunkt nehmen wir den Koordinatenursprung, als Torusachse die y-Achse.
Dieser Torus hat die implizite Gleichung:
![]() (1)
(1)
Herleitung
der impliziten Gleichung: Wir schneiden den Torus mit zur x,z-Ebene parallelen Ebenen im Abstand ![]() . Dies ergibt vier Kreise mit den Radien
. Dies ergibt vier Kreise mit den Radien ![]() . Diese haben somit die Gleichungen:
. Diese haben somit die Gleichungen:
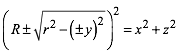 (2)
(2)
Durch Quadrieren und Wegmachen der Wurzeln erhalten wir daraus (1).
Die Abbildung 1 zeigt einen Torus mit R = 2 und r = 0.5. In der Abbildung 1a) wurde mit der impliziten Gleichung (1) mit 12×6×12 Gitterpunkten gearbeitet. Die Abbildung 1b) zeigt eine geglttete Version.
Natrlich kann man den Torus auch mit einer Parameterdarstellung beschreiben. Fr unsere Zwecke ist aber die implizite Koordinatengleichung sachdienlicher.
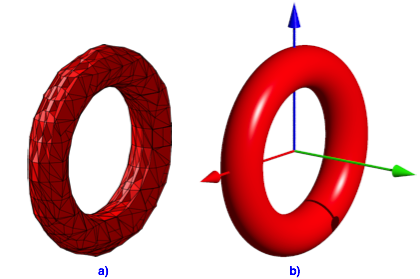
Abb. 1: Torus
Nun tauchen wir den Torus ins Wasser, bis die Wasseroberflche den Kehlkreis erreicht (Abb. 2).
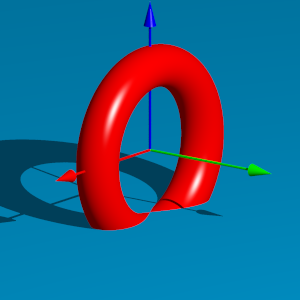
Abb. 2: Eintauchen
Die Schnittfigur auf der Wasseroberflche ist eine 8-frmige Kurve. Allerdings sind haben wir im Doppelpunkt keine rechten Winkel wie das fr die BernoulliÕsche Lemniskate der Fall sein msste.
3 Die BernoulliÕsche Lemniskate
Die BernoulliÕsche Lemniskate erhalten wir fr ein Radienverhltnis R:r = 2:1.
Die Abbildung 3 zeigt die Situation fr R = 1 und r = 0.5.
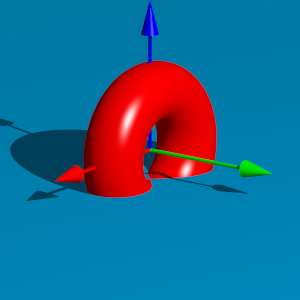
Abb. 3: BernoulliÕsche Lemniskate
Wir haben zu zeigen, dass sich im Doppelpunkt rechte Winkel ergeben.
3.1 Anschaulicher Beweis mit viel Symmetrie und etwas Differentialgeometrie
Bei einem Radienverhltnis R:r = 2:1 ist der Kehlkreis gleich gro§ wie ein Meridiankreis. In einem Kehlkreispunkt haben wir also entgegengesetzt gleiche Hauptkrmmungen. Die DupinÕsche Indikatrix ist eine gleichseitige Hyperbel. Die Asymptotenrichtungen sind orthogonal. Das sind aber auch die Tangentenrichtungen im Doppelpunkt.
3.2 Rechnerischer Beweis
Wir arbeiten mit R = 1 und r = 0.5. Aus (1) ergibt sich dafr die Torusgleichung:
![]() (3)
(3)
Die
Wasseroberflche hat die Gleichung ![]() . Eingesetzt in (3) erhalten wir:
. Eingesetzt in (3) erhalten wir:
![]() (4)
(4)
Dies ist die Gleichung der BernoulliÕschen Lemniskate.
4 Torus und Kugeln
Die Idee ist, den Torus durch eine Folge von Kugeln zu ersetzen.
Die Abbildung 4a zeigt die Situation mit sechs Kugeln. Zwei Kugeln berhren die Wasseroberflche, zwei schneiden einen Kreis heraus (Abb. 4b).
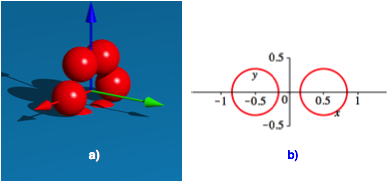
Abb. 4: Sechs Kungeln
Die Abbildung 5 zeigt die Situation mit zwlf Kugeln. Die Kugeln und entsprechend die Kreise berschneiden sich. Sechs der zwlf Kugeln haben Wasserkontakt.
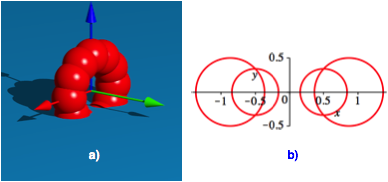
Abb. 5: Zwlf Kugeln
Die Abbildung 6 zeigt die Situation mit 24 Kugeln. Davon erreichten zwlf die Wasseroberflche.
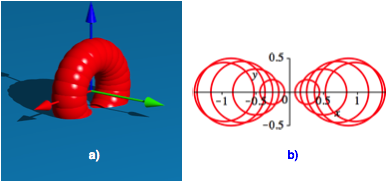
Abb. 6: 24 Kugeln
Die Abbildung 7 zeigt die Schnittkreise bei 96 Kugeln (von denen 48 Wasserkontakt haben). Der Umriss ist die BernoulliÕsche Lemniskate. Man beachte, dass nicht alle Kreise der Kreisschar die Umrisslinie erreichen.

Abb. 7: 96 Kugeln
5 Rechnerisches
Bei 2N Kugeln haben deren N Wasserkontakt.
Wir fhren einen Parameter tn ein:
![]() (5)
(5)
Die Mittelpunkte der 2N Kugeln haben die Koordinaten:
![]() (6)
(6)
Die
Kreise in der x,y-Darstellung haben
die Mittelpunktkoordinaten ![]() und die
Radien:
und die
Radien:
![]() (7)
(7)
Fr ![]() wird der
Radius (7) rein imaginr (die Kugeln sind oberhalb des Wasserspiegels), fr
wird der
Radius (7) rein imaginr (die Kugeln sind oberhalb des Wasserspiegels), fr ![]() reell.
reell.
Wir ndern (7) ab in:
![]() (8)
(8)
Damit
haben wir auch fr ![]() reelle
Werte (welche geometrische Bedeutung haben diese?).
reelle
Werte (welche geometrische Bedeutung haben diese?).
Die Abbildung 8 zeigt die erweiterte Kreisschar.
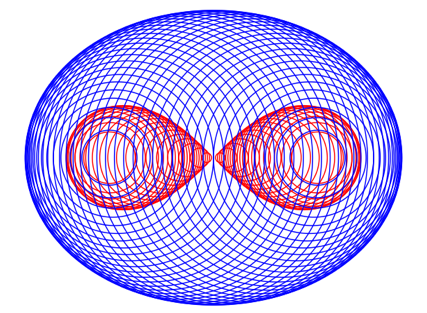
Abb. 8: Erweiterte Kreisschar
Die Enveloppe der erweiterten Kreisschar sieht aus wie eine Ellipse, ist aber keine [6] .
Literatur
Haftendorn, Drte (2017): Kurven erkunden und verstehen. Mit GeoGebra und anderen Werkzeugen. Wiesbaden: Springer Spektrum. ISBN 978-3-658-14748-8.
Luchli, Juan (2020): Die BernoulliÕsche Lemniskate im Unterricht. VSMP Bulletin. Januar 2020, No 142, S. 6-11.
Websites
[1] Hans Walser: Lemniskate (abgerufen 23.02.2020):
http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate/Lemniskate.htm
[2] Hans Walser: Lemniskate (abgerufen 23.02.2020):
http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate2/Lemniskate2.htm
[3] Hans Walser: Lemniskate (abgerufen 23.02.2020):
http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate3/Lemniskate3.htm
[4] Hans Walser: Lemniskatenmodell (abgerufen 23.02.2020)
http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskatenmodell/index.html
[5] Hans Walser: Lemniskatoid (abgerufen 23.02.2020)
http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskatoid/Lemniskatoid.htm
[6] Hans Walser: Eilinie (abgerufen 27.02.2020)
http://www.walser-h-m.ch/hans/Miniaturen/E/Eilinie/Eilinie.htm