Hans Walser, [20191007]

Lemniskatenmodell

Anregung: Juan Läuchli, Frauenfeld

1 Worum geht es?

Die Lemniskate von Jacob Bernoulli (Abb. 1) kann mechanisch mit einem Gelenkmodell realisiert werden. Es wird die Frage untersucht, wie das Problem mit dem „toten Punkt“ angegangen werden kann.

2 Die Lemniskate von Bernoulli

Abb. 1: Lemniskate

Die Lemniskate kann wie folgt definiert werden. Die beiden schwarzen Punkte haben den Abstand 2. Die Lemniskate ist die Menge der Punkte, deren Produkt der Abstände von den beiden schwarzen Punkten 1 ist.

3 Gelenkmodell

Die Abbildung 2 zeigt das Gelenkmodell zur Generierung der Lemniskate in verschiedenen Positionen.

An die beiden schwarzen Punkte der Abbildung 1 sind je ein Hebelarm der Länge angeschlossen. Die Endpunkte dieser Hebelarme sind mit einer gelenkig angebrachten Strecke der Länge 2 verbunden. Der Mittelpunkt dieser Strecke bewegt sich auf der Lemniskate.

Die beiden an die schwarzen Punkte angeschlossenen Hebelarme drehen gegenläufig, aber mit zueinander variablen Drehgeschwindigkeiten. Der an den schwarzen Punkt rechts angeschlossene Hebelarm dreht in der Figurenfolge der Abbildung 2 im positiven Drehsinn, der an den schwarzen Punkt links angeschlossene Hebelarm im negativen Drehsinn.

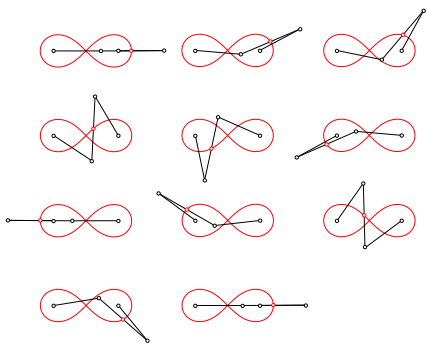
Abb. 2: Gelenkmodell

Das funktioniert in der Theorie und auch im Internet sehr schön.

4 Der tote Punkt

Wir haben aber zwei sogenannte „tote Punkte“. In der Abbildung 2 ist es die Startsituation und dann die Situation im Bild links in der dritten Zeile. In diesen toten Punkten liegen alle Gelenkpunkte und Gelenkteile auf einer Geraden.

Die Startsituation macht keine Probleme, wenn wir den am schwarzen Punkt rechts angeschlossenen Hebelarm im positiven Drehsinn zu drehen beginnen. Es läuft alles gut bis zum zweiten toten Punkt. Dann passiert Folgendes (Abb. 3).

Abb. 3: Nach dem toten Punkt

Der an den schwarzen Punkt links angeschlossene Hebelarm „fällt herunter“. Er ändert die Drehrichtung und dreht nun ebenfalls im positiven Drehsinn. Dadurch entsteht ein Parallelogramm, und der rote Punkt bewegt sich auf einem Kreis.

Das entsprechende Phänomen tritt auch beim Zeichnen mit Dynamischer Geometrie-Software auf. Das liegt daran, dass die Software beim Verändern mit dem Zugmodus nicht entscheiden kann, welcher der beiden Schnittpunkt von zwei Kreisen der „richtige“ ist. Für eine Animation muss man den Vorgang in Teile zerlegen und dann in der Animation wieder zusammenfügen.

Dieser Studie ist eine Animation1(GeoGebra) zum Download beigegeben, welche aus zwei hintereinander ausgeführten Teilanimationen besteht. Der Übergang findet bei den toten Punkten statt. Dabei wird der Hebelarm rechts im schwarzen Punkt rechts angetrieben und bewegt das ganze Gelenkmodell. Der Bewegungsablauf ist asymmetrisch. Der Hebelarm rechts wird gleichmäßig gedreht, der Hebelarm links aber nicht.

In der ebenfalls dieser Studie beigegebenen Animation2 wir geschummelt. Der Lemniskatenpunkt wird mit einer Parameterdarstellung gegeben. Von diesem Punkt aus wird das Gelenkmodell angehängt. Das Gelenkmodell arbeitet daher zwar mit variablen Drehgeschwindigkeiten, aber symmetrisch bezüglich der beiden Hebelarme rechts und links. Die Animation ist aus vier Teilanimationen zusammengesetzt.

5 Historische Bemerkung

Tote Punkte gibt es bei Kolbenmotoren.

Bei ganz alten Dampfmaschinen mit nur einem Kolben wurde das Problem mit einem Schwungrad gelöst, welches die Drehrichtung aufrechterhielt.

Bei Maschinen mit mehr als einem Kolben kann durch ein Winkelversatz erreicht werden, dass immer nur eine Pleuelstange im toten Punkt ist, die anderen aber arbeiten können.

6 Überlistung der Schwerkraft

Ich habe das Problem mechanisch so gelöst, dass ich den einen Hebelarm festhielt, dafür die Referenzfigur mit der Lemniskate drehte. Dadurch fällt der andere Hebelarm immer auf die richtige Seite. Die Abbildungsfolge 4 zeigt einige Positionen des mechanischen Modells.

Die an den schwarzen Punkten (Abb. 2) angeschlossenen Hebelarme sind aus Plexiglas. Der eine Hebelarm zeigt fest nach links oben.

Die Verbindungsstrecke ist als Quadratdiagonale realisiert, das Quadrat ebenfalls aus Plexiglas. Mit diesem Quadrat-Trick bringt man das an sich irrationale Verhältnis in den Raster. Der Mittelpunkt ist durch eine Schraube mit unterlegter Messingscheibe markiert. Er bewegt sich längs der Lemniskate. Da der Mittelpunkt und die Lemniskate auf verschiedenen Ebenen liegen, haben wir in den Fotos teilweise Parallaxen, das heißt der Mittelpunkt liegt in der Foto nicht immer genau vor der Lemniskate.

Abb. 4.1: Startposition

Abb. 4.2: Verdrehung der Lemniskatenebene

Abb. 4.3

Abb. 4.4

Abb. 4.5

Abb. 4.6

Abb. 4.7

Abb. 4.8

Abb. 4.9

Abb. 4.10

Das Modell funktioniert nur in einer Drehrichtung. Wenn man umgekehrt kurbelt, entstehen Parallelogramme, und der Mittelpunkt bewegt sich auf einem Kreis.

Websites

Hans Walser: Winkeldrittelung mit Lemniskate

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung5/Winkeldrittelung5.htm

Hans Walser: Lemniskate

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate/Lemniskate.htm

Hans Walser: Lemniskate

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate2/Lemniskate2.htm

Hans Walser: Lemniskate

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate3/Lemniskate3.htm

Hans Walser: Lemniskatoid

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskatoid/Lemniskatoid.htm

Lieratur

Walser, Hans (2018): Die Acht in der Kugel. MU, Der Mathematikunterricht. Jahrgang 64. Heft 4-2018. S. 50-55. ISSN 0025-5807.