Hans Walser, [20160929]
Lemniskatoid
1 Worum geht es?
Topologische Fragen (Orientierbarkeit) einer speziellen Rotationsflche
2 Das Lemniskatoid
Wir drehen eine liegende Acht (der Autor hat die Lemniskate genommen, das ist aber unwesentlich) um eine senkrechte Achse durch den Kreuzungspunkt (Abb. 1).
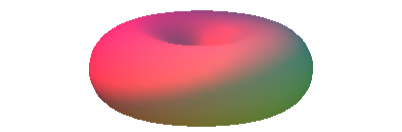
Abb. 1: Lemniskatoid
Die Abbildung 2 zeigt einen Achsenschnitt.
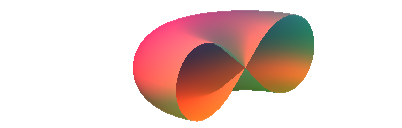
Abb. 2: Achsenschnitt
Topologisch gesehen ist die Lemniskate die bergangsstelle vom Torus zur Sphre.
Die Abbildung 3 zeigt den Achsenschnitt in der x,z-Ebene.

Abb. 3: Lemniskate
3 Orientierbarkeit
Wir gehen der Frage nach, ob das Lemniskatoid orientierbar ist.
3.1 Lngs eines Meridians
Lo
duca e io per quel cammino ascoso
intrammo a ritornar nel chiaro
mondo;
e sanza cura aver d'alcun riposo,
salimmo s,
el primo e io secondo,
tanto ch'i' vidi de le cose
belle
che porta 'l ciel, per un
pertugio tondo.
Dante, La Divina Commedia
Inferno, Canto XXXIV
Prima vista hat man den Eindruck, man knne lngs eines Meridians beim Durchgang durch den Kreuzungspunkt vom Inneren ins u§ere gelangen und umgekehrt.
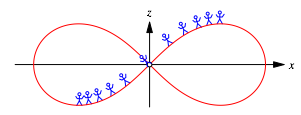
Abb. 4: Durchgang
Damit wre das Lemniskatoid nicht orientierbar und so eine schne Sache wie die Kleinsche Flasche.
Damit haben wir allerdings die Rechnung ohne unsere Existenzgrundlage, eben das Lemniskatoid, gemacht.
3.2 Kreuzende Meridiane
E
pi corusco e con pi lenti passi
teneva il sole il cerchio di merigge,
che
qua e l, come li aspetti, fassi,
quando s'affisser, s come s'affigge
chi va
dinanzi a gente per iscorta
se
trova novitate o sue vestigge,
le
sette donne al fin d'un'ombra smorta,
qual
sotto foglie verdi e rami nigri
sovra
suoi freddi rivi l'alpe porta.
Dante, La Divina Commedia
Purgatorio,
Canto XXXIII
Die Abbildung 5 zeigt einen Ausschnitt beim Kreuzungspunkt.
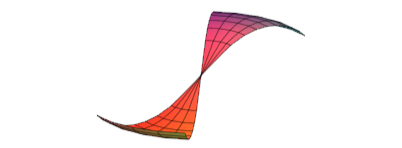
Abb. 5: Ausschnitt
Ein durch zwei Meridiane begrenzter Streifen verhlt sich beim Kreuzungspunkt wie ein Mbiusband. Er wird getwistet. Ein Wanderer auf diesem Streifen wird mitgedreht und befindet sich nach dem Durchgang wieder auf derselben Seite wie vorher (Abb. 6).
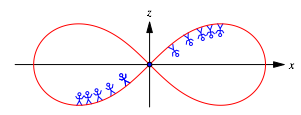
Abb. 6: Da gibt es kein Entrinnen
Somit ist das Lemniskatoid orientierbar.
4 Ausdehnung
Wir modifizieren unsere Flche wie folgt. Wir beginnen mit einem halben Lemniskatoid (Abb. 2) und setzen einen liegenden Lemniskatenzylinder an (Abb. 7).

Abb. 7: Ansetzen eines Lemniskatenzylinders
Im Zylinderteil knnen wir gem§ Abbildung 4 von innen nach au§en gelangen, ohne Mbius-Twist. Die Gesamtflche der Abbildung 7 ist daher nicht mehr orientierbar.
Der Symmetrie zuliebe schlie§en wir die Flche mit einem zweiten halben Lemniskatoid ab (Abb. 8).
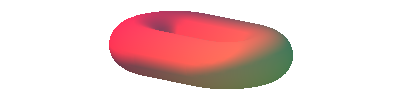
Abb. 8: Abschluss
Die Abbildung 9 zeigt einen Ausschnitt aus der Flche der Abbildung 8. Der Ausschnitt ist ein Mbius-Band.
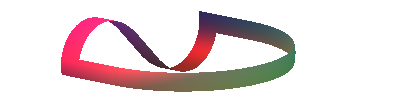
Abb. 9: Mbius-Band
5 Nachtrag: Stehendes Lemniskatoid
Natrlich htten wir dieselben berlegungen auch am stehenden Lemniskatoid (Abb. 10) durchfhren knnen.
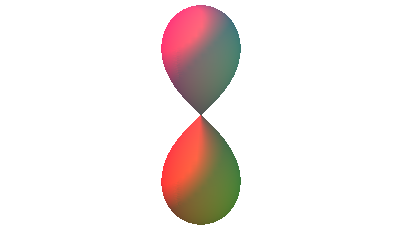
Abb. 10: Hora incerta