1 Worum geht es?

Definitionen und eine Eigenschaft der Lemoine-Gerade. Schnittpunkte. Verifikation mit DGS.

2 Der Lemoine-Punkt

In einem beliebigen Dreieck ABC ist der Lemoine-Punkt L (auch Grebe-Punkt genannt) derjenige Punkt, der von den drei Seiten a,b,c Abstände im Verhältnis a:b:c hat.

Konstruktion (Abb. 1): Wir setzen dem Dreieck (gelb in Abb. 1) hellblaue Quadrate an. Dies hat aber nichts mit Pythagoras zu tun, das Dreieck ist im Regelfall nicht rechtwinklig.

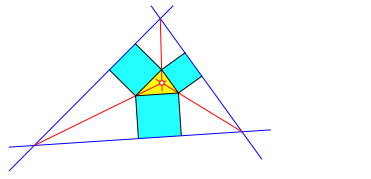
Abb. 1: Lemoine-Punkt

Wir verlängern die Außenkanten der Quadrate bis zum Schnittpunkt. Die roten Geraden durch diese Schnittpunkte und die naheliegenden Dreiecksecken schneiden sich ein einem Punkt. Dies ist der Lemoine-Punkt L.

3 Die Lemoine-Gerade

Die Lemoine-Gerade ist die Gerade durch den Lemoine-Punkt L und den Umkreismittelpunkt des Dreiecks (Abb. 2).

Abb. 2: Lemoine-Gerade

4 Apollonius-Kreise

Wir zeichnen zu jeder Dreiecksseite den Apollonius-Kreis für das Teilverhältnis der beiden anderen Seiten (violett in Abb. 3). Die Apollonius-Kreise finden wir mit den inneren und äußeren Winkelhalbierenden, die wir mit den Gegenseiten schneiden. Die Apollonius-Kreise sind die Thaleskreise über den durch die Winkelhalbierenden herausgeschnittenen Strecken.

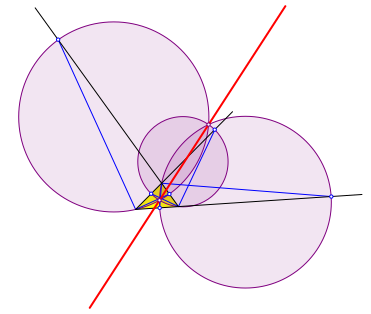
Abb. 3: Apollonius-Kreise

Die drei Apollonius-Kreise haben zwei Schnittpunkte gemeinsam. Diese liegen auf der Lemoine-Geraden.

5 Ansetzen von Fünfecken

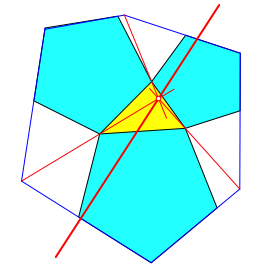
Abb. 4: Fünfecke ansetzen

Wir setzen Fünfecke an und schneiden die verlängerten Dachschrägen. Die roten Geraden durch diese Schnittpunkte und die naheliegenden Dreiecksecken schneiden sich ein einem Punkt. Dieser Punkt liegt auf der Lemoine-Geraden.

Es geht analog mit beliebigen regelmäßigen n-Ecken mit n ≥ 4.

6 Allgemein

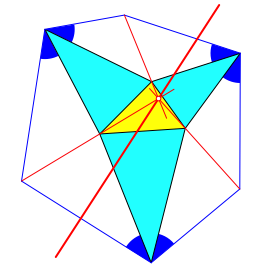
Abb. 5: Allgemein

Wir setzen beliebige, aber ähnliche gleichschenklige Dreiecke auf. An der Spitze tragen wir auf beiden Seiten den gleichen Winkel ab und schneiden die entstehenden zweiten Winkelschenkel. Die roten Geraden durch diese Schnittpunkte und die naheliegenden Dreiecksecken schneiden sich ein einem Punkt. Dieser Punkt liegt auf der Lemoine-Geraden.

7 Sonderfälle

Wenn wir die Basiswinkel der gleichschenkligen Dreiecke abtragen, ergibt sich der Lemoine-Punkt.

Wenn wir nach innen den halben Spitzenwinkel abtragen (also die Symmetrieachsen der gleichschenkligen Dreiecke nehmen), ergibt sich der Mittelsenkrechtenschnittpunkt, also der Mittelpunkt des Umkreises.

Die beiden definierenden Punkte der Lemoine-Geraden sind also in dieser Konstruktion enthalten.

Websites

Hans Walser: Schnittpunkte 801-900

http://www.walser-h-m.ch/hans/Schnittpunkte/Schnittpunkte_801-900.htm