Hans Walser, [20220928]
Linsenträger Hyperwürfel
1 Worum geht es?
Zweidimensionale Darstellung des n-dimensionalen Hyperwürfels.
2 Grundidee
Wir arbeiten mit n Basisvektoren v1, v2, v3, ... , vn unterschiedlicher Steigung und benützen diese als Einheitsvektoren für Einheits-Hyperwürfel.
3 Beispiel vierdimensionaler Hyperwürfel
3.1 Basisvektoren
Die vier Basisvektoren haben der Reihe nach die Steigungen 1, 2, 4, 8, also ein exponentielles Wachstum der Steigungen (Abb. 1). Um schönere Bilder zu erhalten, können die beiden Koordinatenachsen unterschiedlich skaliert werden. Die Pfeilspitzen werden dabei allerdings verzerrt dargestellt.
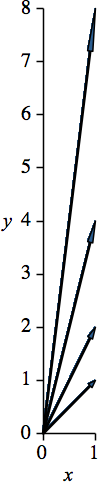
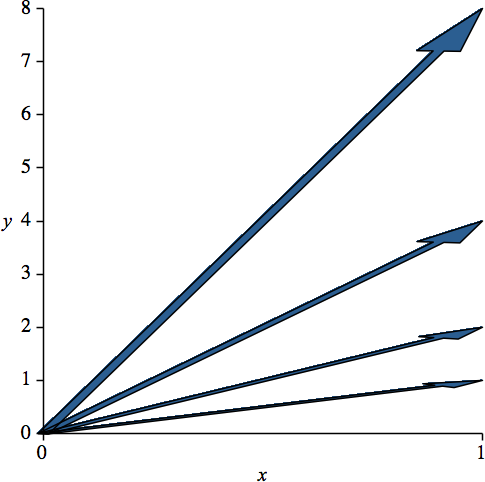
Abb. 1: Exponentielles Wachstum der Steigungen. Gleiche und unterschiedliche Achsenskalierung
3.2 Eckpunktkoordinaten
Die 24 = 16 Eckpunkte des vierdimensionalen Einheits-Hyperwürfels haben die Koordinaten der Tabelle 1:
[0, 0, 0, 0]
[1, 0, 0, 0]
[0, 1, 0, 0]
[1, 1, 0, 0]
[0, 0, 1, 0]
[1, 0, 1, 0]
[0, 1, 1, 0]
[1, 1, 1, 0]
[0, 0, 0, 1]
[1, 0, 0, 1]
[0, 1, 0, 1]
[1, 1, 0, 1]
[0, 0, 1, 1]
[1, 0, 1, 1]
[0, 1, 1, 1]
[1, 1, 1, 1]
Tab. 1: Koordinaten der Eckpunkte
3.3 Bilder der Eckpunkte
Die Bilder der Eckpunkte erhalten wir nun durch Linearkombination der vier Vektoren gemäß den Eckpunktkoordinaten.
Beispiel: Zum Punkt mit den Koordinaten [1, 0, 1, 1] gehört der Bildpunkt 1v1 + 0v2 + 1v3 + 1v4.
Die Abbildung 2 zeigt die Situation mit den Koordinaten.
Die Summe der Koordinaten eines Punktes ist der horizontale Abstand (also der Abstand in der x-Richtung) von der y-Achse.
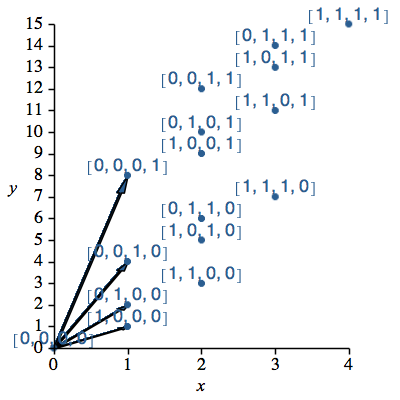
Abb. 2: Eckpunkte mit Koordinaten
3.4 Bilder der Kanten
Zwei Eckpunkte sind genau dann durch eine Kante verbunden, wenn ihre Koordinaten sich an genau einer Stelle unterscheiden (Abb. 3).
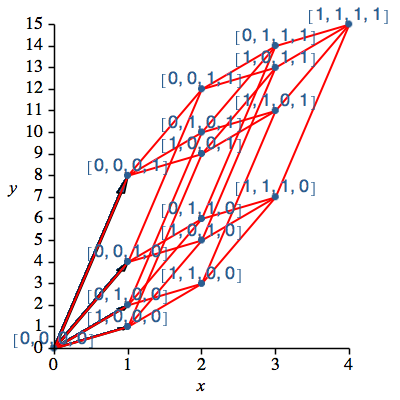
Abb. 3: Kanten
4 Exkurs: Hamming-Distanz
Unter der Hamming-Distanz zweier Punkte verstehen wir in unserem Kontext die Anzahl unterschiedlicher Koordinaten der beiden Punkte.
Die Summe der Koordinaten eines Punktes ist die Hamming-Distanz des Punktes vom Punkt [0, 0, 0, 0].
Da in unserem Kontext nur die Koordinaten 0 und 1 vorkommen, ist die mit Pythagoras berechnete Distanz zweier Punkte die Quadratwurzel aus der Hamming-Distanz. Dies gilt natürlich nur im n-dimensionalen Raum, nicht in unserer zweidimensionalen Darstellung.
Beispiel: Punkte mit der Hamming-Distanz 2 haben die gewöhnliche Distanz √2. Ihre Verbindung ist eine Quadratdiagonale. Die Abbildung 4 zeigt sämtliche Quadratdiagonalen (in magenta).
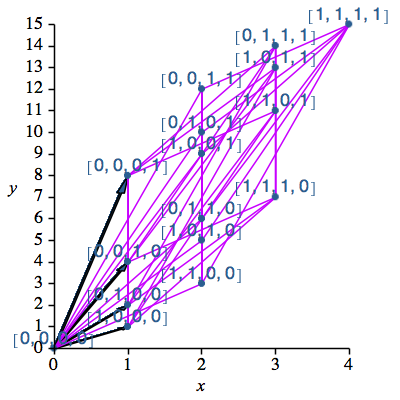
Abb. 4: Quadratdiagonalen
5 Eckennummern
Wir interpretieren die Koordinaten der Ecken als Dualzahlen in umgekehrter Reihenfolge der Schreibweise.
Beispiele:
[0, 0, 1, 0] interpretieren wir als Dualzahl 0100, somit als Dezimalzahl 4.
[1, 0, 1, 1] interpretieren wir als Dualzahl 1101, somit als Dezimalzahl 13.
Die Abbildung 5 zeigt den vierdimensionalen Hyperwürfel mit den Eckennummern in dezimaler Schreibweise. Die Eckennummern entsprechen in unserer Darstellung dem Niveau in y-Richtung.
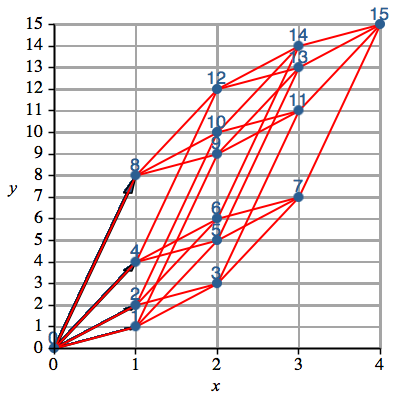
Abb. 5: Eckennummern
6 Diskussion
Das Bild eines Punktes finden wir nun wir folgt: Die Summe der Koordinaten ist die x-Koordinate des Bildpunktes. Die Interpretation der Koordinaten als Dualzahl in umgekehrter Reihenfolge ist die y-Koordinate des Bildpunktes. Umgekehrt können wir jedem Bildpunkt eindeutig die Koordinaten zuordnen. Es wird also jeder Punkt einzeln dargestellt.
Bei der x-Koordinate 0 haben wir nur einen Punkt.
Bei der x-Koordinate 1 haben wir vier Punkte.
Bei der x-Koordinate 2 haben wir sechs Punkte.
Bei der x-Koordinate 3 haben wir vier Punkte.
Bei der x-Koordinate 4 haben wir nur einen Punkt.
Die Anzahlen 1, 4, 6, 4, 1 sind die Binomialkoeffizienten für n = 4.
7 Exponentielle Darstellung
Die Abbildung 6 ist auf das Wesentliche beschränkt. Die Punkte am unteren Rand liegen auf einer Exponentialkurve, daher die Bezeichnung exponentielle Darstellung. Die Figur ist punktsymmetrisch.
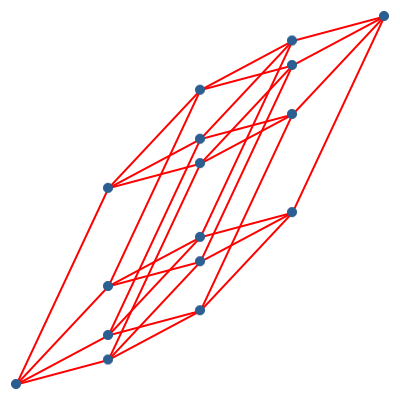
Abb. 6: Vierdimensionaler Hyperwürfel
Die Abbildung 7 zeigt die exponentielle Darstellung für die Dimensionen 1 bis 7.

Abb. 7: Exponentielle Darstellung
8 Linsenträger-Darstellung
Durch eine Scherung können wir erreichen, dass der Punkt rechts oben auf dasselbe Niveau wir der punkt links unten zu liegen kommt (Abb. 8). Die Darstellung erinnert an ein Linsenträger-Fachwerk im Brückenbau.
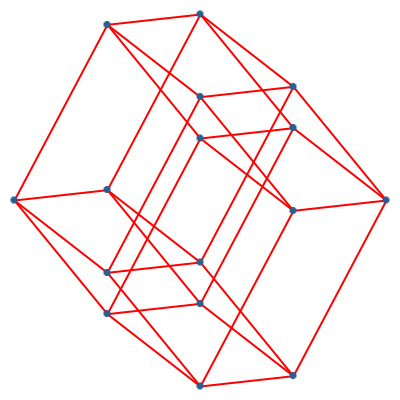
Abb. 8: Linsenträger-Darstellung des vierdimensionalen Hyperwürfels
Die Abbildung 9 zeigt die Situation für die Dimensionen 1 bis 7.

Abb. 9: Dimensionen 1 bis 7
9 Lineare Basisvektoren
Wir wählen nun die Basisvektoren so, dass ihre Steigung linear zunimmt (Abb. 10).
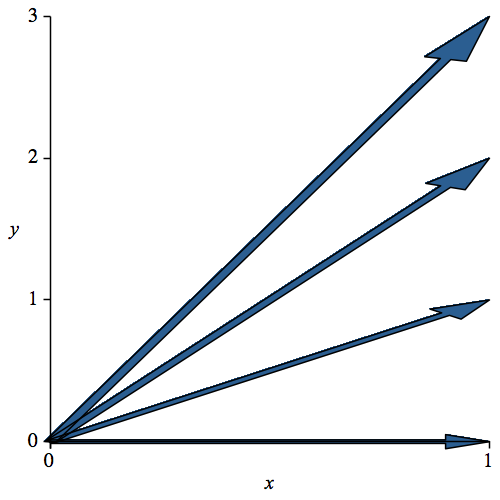
Abb. 10: Lineare Zunahme der Steigung
Die Abbildung 11 zeigt die entsprechende Darstellung des vierdimensionalen Hyperwürfels.
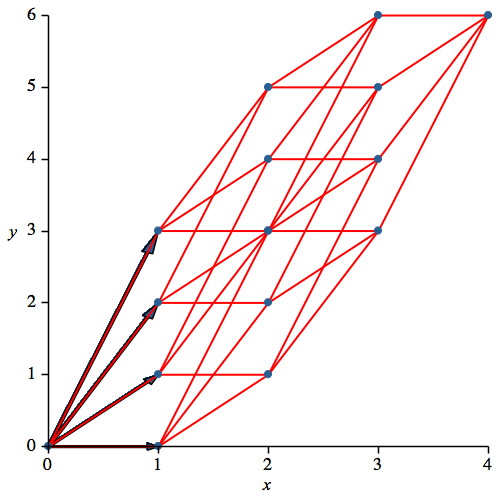
Abb. 11: Vierdimensionaler Hyperwürfel
Bei der Hamming-Distanz 2 vom Startpunkt (also bei x = 2) haben wir nur noch 5 statt 6 Punkte. Dies kommt daher, dass in der Darstellung zwei Punkte aufeinanderfallen. Wir können also nicht mehr die Koordinaten eindeutig rekonstruieren. Es sind die Punkte 6 und 9, die aufeinanderfallen (Abb. 12).
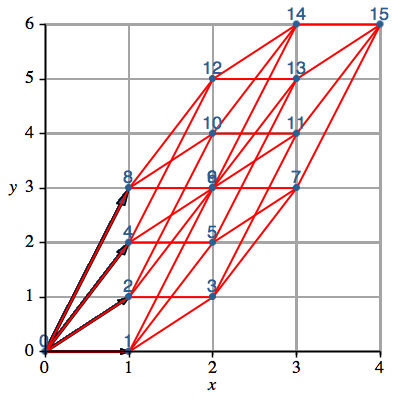
Abb. 12: Aufeinanderfallende Punkte
Die Abbildung 13 zeigt die entsprechende Darstellung für die Dimensionen 1 bis 7.

Abb. 13: Lineare Darstellung
10 Lineare Linsenträger-Darstellung
Die Abbildung 14 zeigt die zugehörige lineare Linsenträger-Darstellung für den vierdimensionalen Hyperwürfel. Wir haben mehr Symmetrien als bei der exponentiellen Linsenträger-Darstellung.
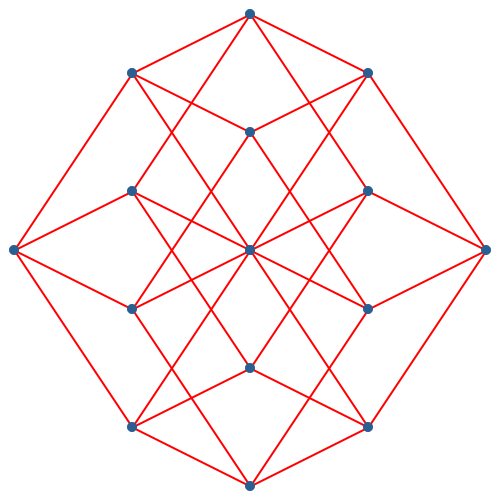
Abb. 14: Lineare Linsenträger-Darstellung des vierdimensionalen Hyperwürfels
Die Abbildung 15 zeigt die Darstellung für die Dimension 7. Der Autor gesteht, dass er die vorliegende Studie wegen diesem Bild geschrieben hat.
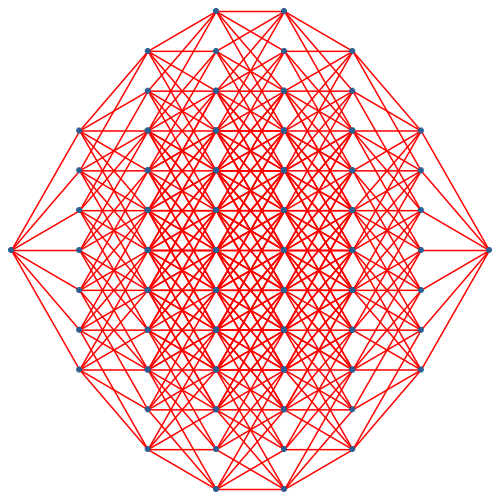
Abb. 15: Lineare Linsenträger-Darstellung des siebendimensionalen Hyperwürfels
Die Abbildung 16 zeigt eine Animation für die Dimensionen 1 bis 7.

Abb. 16: Dimensionen 1 bis 7
11 Übergang
Wir können von der exponentiellen Darstellung zur linearen Darstellung übergehen. Die Abbildung 17 zeigt dies für die Dimension 4. Wir sehen, wie die beiden Punkte in der Mitte zusammenkommen.
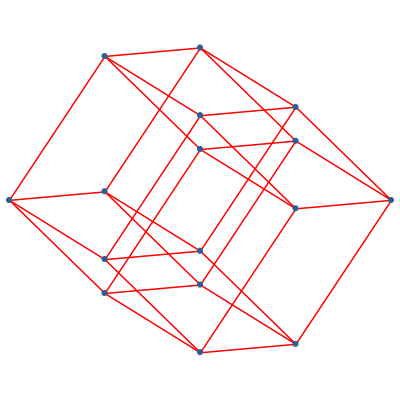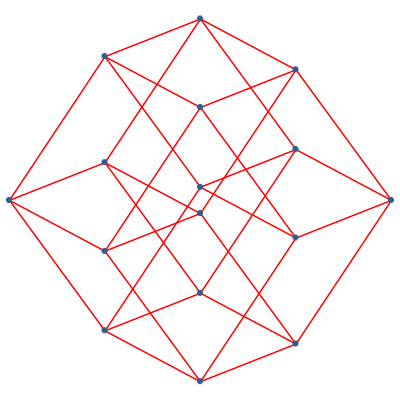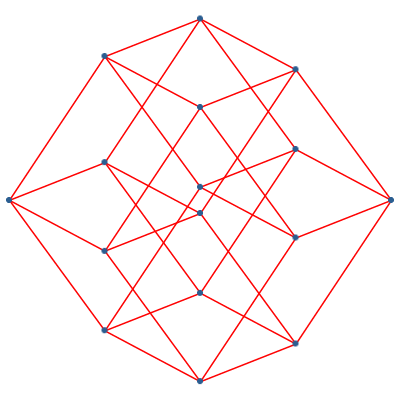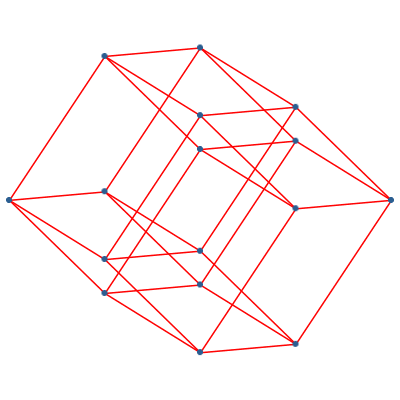
Abb. 17: Darstellungen des vierdimensionalen Hyperwürfels
Die Abbildung 18 zeigt das Entsprechende für die Dimension 7.

Abb. 18: Darstellungen des siebendimensionalen Hyperwürfels
Weblinks
Hans Walser: Diagonalen im Hyperwürfel
Hans Walser: Eckennummerierung von Hyperwürfeln
http://www.walser-h-m.ch/hans/Miniaturen/E/Eckennummerierung/Eckennummerierung.html
Hans Walser: Hypercubus
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel/Hyperwuerfel.pdf
Hans Walser: Hyperwürfel
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel4/Hyperwuerfel4.html
Hans Walser: Hyperwürfel
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel3/Hyperwuerfel3.html
Hans Walser: Hyperwürfel
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel2/Hyperwuerfel2.htm
Hans Walser: Kollineare Punkte
http://www.walser-h-m.ch/hans/Miniaturen/K/Kollineare_Punkte6/Kollineare_Punkte6.html
Hans Walser: Simplex
http://www.walser-h-m.ch/hans/Miniaturen/S/Simplex2/Simplex2.html