0 Worum geht es?

Räumliche Analogie zu den Lissajous-Figuren in der Ebene

Schöne Bildchen

1 Die Parameterdarstellung

Wir arbeiten mit der Parameterdarstellung:

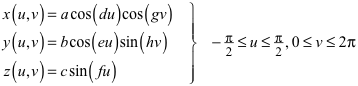(1)

Wir haben acht freie Koeffizienten: a, b, c, d, e, f, g, h

Werden alle Koeffizienten auf 1 gesetzt, ergibt sich die Kugel in der üblichen Parametrisierung.

Abb. 1: a = 1, b = 1, c = 1 , d = 1, e = 1, f = 1 , g = 1 , h = 1

Abb. 2: a = 1, b = 1, c = 1 , d = 2, e = 1, f = 1 , g = 1 , h = 1

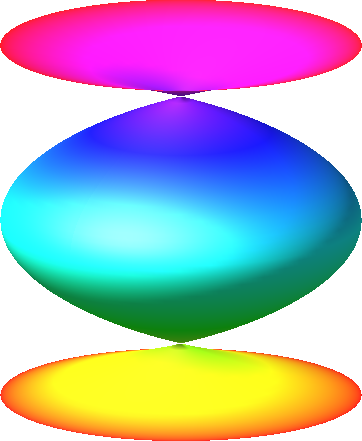
Abb. 3: a = 1, b = 1, c = 1 , d = 2, e = 2, f = 1 , g = 1 , h = 1

Ein Bild, das Sitz, Stuhl, Hocker, Vektorgrafiken enthält.

Automatisch generierte Beschreibung

Abb. 4: a = 1, b = 1, c = 1 , d = 2, e = 3, f = 1 , g = 1 , h = 1

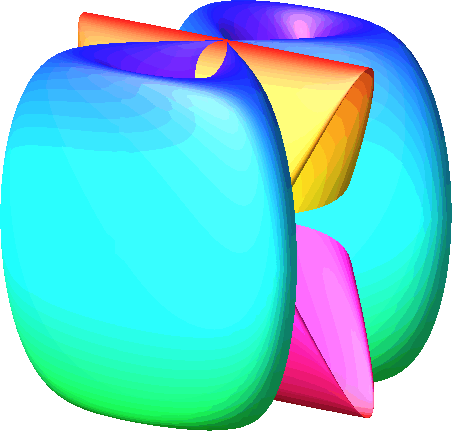
Abb. 5.1: a = 1, b = 1, c = 1 , d = 1, e = 2, f = 3 , g = 1 , h = 2

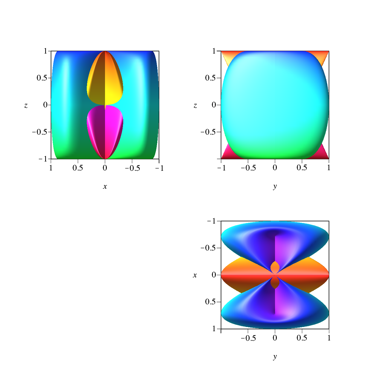
Abb. 5.2: Klassische Risse

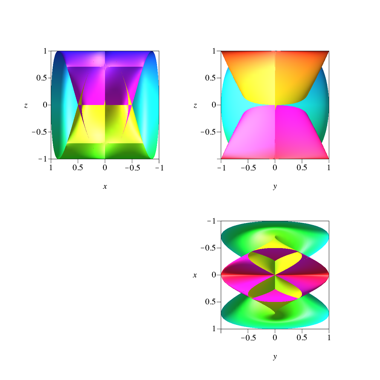
Abb. 5.3: Halbe Sichten

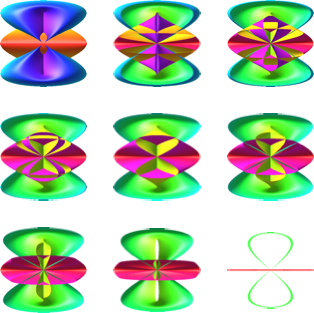
Abb. 5.4: Schnittfolge

Abb. 5.5: Schnittfolge

Abb. 5.6: Genesis-Animation Parameter u

Abb. 5.7: Genesis-Animation Parameter v

Abb. 6: a = 1, b = 1, c = 1 , d = 1, e = 2, f = 3 , g = 1 , h = 3

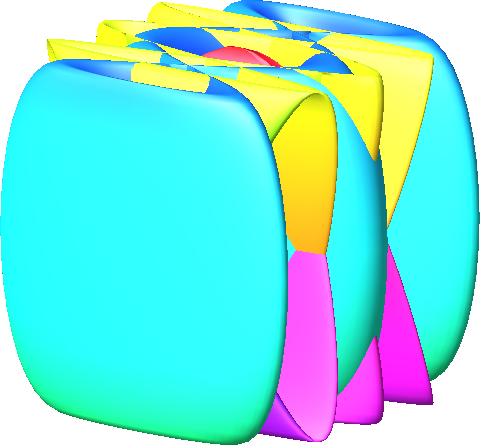
Ein Bild, das Zubehör enthält.

Automatisch generierte Beschreibung

Abb. 7: a = 1, b = 1, c = 1 , d = 1, e = 3, f = 5 , g = 1 , h = 3

Abb. 8: a = 1, b = 1, c = 1 , d = 1, e = 3, f = 5 , g = 1 , h = 3

Websites

Hans Walser: 3d-Lissajous

Hans Walser: nd-Kreis