Hans Walser, [20200716]
Logarithmische Kantenmittenspirale
Anregung: M. E., B.
1 Worum geht es
Gesucht ist eine eckige logarithmische Spirale aus Streckenzgen, welche sich selber in- und umbeschrieben ist und sich in den Kantenmitten berhrt.
2 Beispiel

Abb. 1: Beispiel
Die Abbildung 1 zeigt eine eckige logarithmische Spirale. Die Streckenlngen nehmen schrittweise um denselben Faktor q = 0.9691929055 ab. Die Richtungsnderung (Au§enwinkel) ist an jeder Ecke gleich, nmlich 65.35002089¡ im positiven Drehsinn. Der Endpunkt der sechsten Strecke ist der Mittelpunkt der ersten Strecke. Auch alle nachfolgenden Eckpunkte sind Mittelpunkte von Spiralen-Strecken.
Eine eckige logarithmische Spirale ist bis auf hnlichkeit durch den konstanten Lngenvernderungsfaktor q und die konstante Richtungsnderung bestimmt.
Wir fragen nach diesen beiden Bestimmungsdaten unter der zustzlichen Bedingung, dass der Endpunkt der n-ten Strecke der Mittelpunkt der ersten Strecke ist.
3 Die Gleichung
Wir arbeiten exemplarisch fr n = 6 in der Gau§schen Ebene der komplexen Zahlen (Abb. 2). Der Schlssel zu unserer Aufgabe ist die komplexe Zahl z. Ihr Betrag ist der Lngen-Vernderungsfaktor q, ihr Argument die Richtungsnderung.
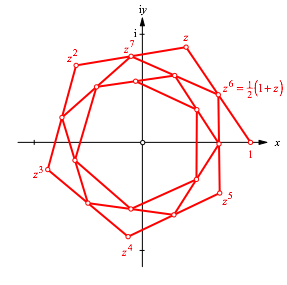
Abb. 2: berlegungsfigur
Die Bedingung, dass der Endpunkt der sechsten Strecke auf den Mittelpunkt der ersten Strecke zu liegen kommen muss, hei§t:
![]() (1)
(1)
Im allgemeinen Fall erhalten wir die Gleichung:
![]() (2)
(2)
4 Lsungsbersicht
Die Gleichung (2) hat nach dem Fundamentalsatz der Algebra in der komplexen Ebene genau n Lsungen.
Eine triviale Lsung ist z = 1. Diese Lsung ist fr uns nicht relevant.
Wir machen eine Parittsunterscheidung bezglich n.
4.1 n gerade
Die Tabelle 1 zeigt exemplarisch die Lsungen fr n = 6. Die Lsungen sind mit dem Index k nummeriert.
|
k |
zk |
|zk| |
arg(zk) |
|
1 |
1 |
1 |
0¡ |
|
2 |
0.4042249299 + 0.8808729160i |
0.9691929055 |
65.35002089¡ |
|
3 |
–0.5440186493 + 0.6655179335i |
0.8595757155 |
129.2638176¡ |
|
4 |
–0.7204125613 |
0.7204125613 |
180¡ |
|
5 |
–0.5440186493 – 0.6655179335i |
0.8595757155 |
-–129.2638176¡ |
|
6 |
0.4042249299 – 0.8808729160i |
0.9691929055 |
–65.35002089¡ |
Tab. 1: Lsungen fr n = 6
Die Abbildung 3 zeigt die Verteilung dieser Lsungen in der Gau§schen Ebene der komplexen Zahlen. Der blaue Kreis ist der Einheitskreis.
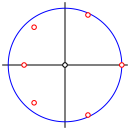
Abb. 3: Lsungen fr n = 6
Neben der trivialen Lsung z1 = 1 haben wir noch eine zweite reelle Lsung. Die brigen Lsungen sind paarweise konjugiert komplex und liegen daher spiegelbildlich bezglich der reellen Achse.
4.2 n ungerade
Die Tabelle 2 zeigt exemplarisch die Lsungen fr n = 7.
|
k |
zk |
|zk| |
arg(zk) |
|
1 |
1 |
1 |
0¡ |
|
2 |
0.5581619009 + 0.8073355575i |
0.9814965155 |
55.34145396¡ |
|
3 |
–0.3174374594 + 0.8613972540i |
0.9180260181 |
110.2295783¡ |
|
4 |
–0.7407244414 + 0.2592065099i |
0.7847679357 |
160.7131957¡ |
|
5 |
–0.7407244414 – 0.2592065099i |
0.7847679357 |
–160.7131957¡ |
|
6 |
–0.3174374594 – 0.8613972540i |
0.9180260181 |
–110.2295783¡ |
|
7 |
0.5581619009 – 0.8073355575i |
0.9814965155 |
–55.34145396¡ |
Tab. 2: Lsungen fr n = 7
Die Abbildung 4 zeigt die Verteilung dieser Lsungen.
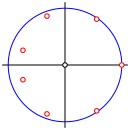
Abb. 4: Lsungen fr n = 7
Die einzige reelle Lsung ist z1 = 1. Die brigen Lsungen sind paarweise konjugiert komplex.
4.3 Hintergrund
Die Gleichung (2) ist eine leicht gestrte Kreisteilungsgleichung. Die (ungestrte) Kreisteilungsgleichung lautet:
![]() (3)
(3)
Die n Lsungen der Kreisteilungsgleichung bilden ein regelm§iges n-Eck auf dem Einheitskreis.
5 Bildergalerie
5.1 n = 6
Die Lsungen beziehen sich auf die Tabelle 1.
Die triviale Lsung z1 = 1 gibt nichts.
Aus der Lsung z2 = 0.4042249299 + 0.8808729160i erhalten wir die Spirale der Abbildung 5.2 (entspricht der Abbildung 1).

Abb. 5.2: Spirale
Aus der Lsung z3 = –0.5440186493 + 0.6655179335i erhalten wir die berschlagene Spirale der Abbildung 5.3.
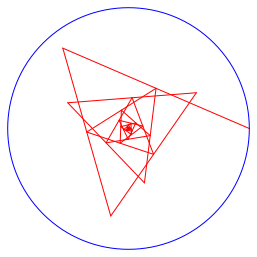
Abb. 5.3: berschlagene Spirale
Die Leserin oder der Leser kann mit dem Finger nachprfen, dass tatschlich der Endpunkt der sechsten Strecke im Mittelpunkt der ersten Strecke liegt (Abb. 5.3a).
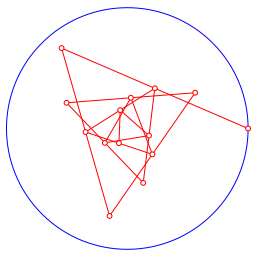
Abb. 5.3a: Endpunkte und Mittelpunkte
Aus der reellen Lsung z4 = –0.7204125613 erhalten wir ein Hin-und-her auf der reellen Achse (Abb. 5.4).
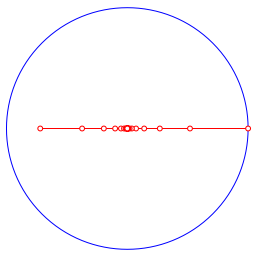
Abb. 5.4: Hin-und-her
Aus der Lsung z5 = –0.5440186493 – 0.6655179335i erhalten wir die berschlagene Spirale der Abbildung 5.5. Sie ist spiegelbildlich zur Spirale der Abbildung 5.3, da die zugehrigen Lsungen konjugiert komplex sind.
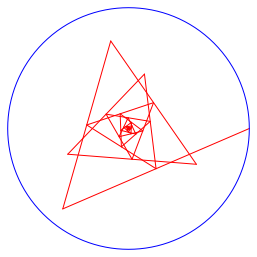
Abb. 5.5: berschlage Spirale
Aus der Lsung z6 = 0.4042249299 – 0.8808729160i erhalten wir die Spirale der Abbildung 5.6. Sie ist spiegelbildlich zur Spirale der Abbildung 5.2.

Abb.5.6: Spirale
5.2 n = 7
Die Lsungen beziehen sich auf die Tabelle 2.
Die triviale Lsung z1 = 1 gibt nichts.
Aus der Lsung z2 = 0.5581619009 + 0.8073355575i erhalten wir die Spirale der Abbildung 6.2.

Abb. 6.2: Spirale
Aus der Lsung z3 = –0.3174374594 + 0.8613972540i erhalten wir die berschlagene Spirale der Abbildung 6.3.

Abb. 6.3: berschlage Spirale
Aus der Lsung z4 = –0.7407244414 + 0.2592065099i erhalten wir die berschlagene Spirale der Abbildung 6.4.

Abb. 6.4: berschlagene Spirale
Aus den weiteren, konjugiert komplexen Lsungen ergeben sich entsprechend spiegelbildliche Spiralen.
5.3 n = 3
Der Fall n = 3 fhrt zu einer bekannten Figur. Zunchst die numerischen Lsungen (Tab. 3).
|
k |
zk |
|zk| |
arg(zk) |
|
1 |
1 |
1 |
0¡ |
|
2 |
–0.5000000000 + 0.5000000000i |
0.7071067810 |
135¡ |
|
3 |
–0.5000000000 – 0.5000000000i |
0.7071067810 |
–135¡ |
Tab. 3: Lsungen fr n = 3
Das sind natrlich exakt darstellbare Werte (Tab. 4).
|
k |
zk |
|zk| |
arg(zk) |
|
1 |
1 |
1 |
0¡ |
|
2 |
|
|
135¡ |
|
3 |
|
|
–135¡ |
Tab. 4: Exakte Werte fr n = 3
Die Abbildung 7 zeigt die Verteilung dieser Lsungen.
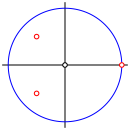
Abb. 7: Lsungen fr n = 3
Aus der
Lsung ![]() erhalten
wir die Spirale der Abbildung 8.2.
erhalten
wir die Spirale der Abbildung 8.2.

Abb. 8.2: Rechtwinklig gleichschenklige Dreiecke
Die Spirale ergibt sich durch fortlaufendes Halbieren eines rechtwinklig gleichschenkligen Dreiecks.
6 Ausblick
Wir knnen die Mittelpunkte ersetzen durch andere Teilpunkte. Wir knnen zum Beispiel verlangen, dass der Endpunkt der n-ten Strecke der erste Drittelpunkt der ersten Strecke wird. Dazu mssen wir die Gleichung (2) abndern in:
![]() (4)
(4)
Die Abbildung 9 zeigt ein Beispiel fr n = 6. Wir glauben dabei noch zustzliche Spiralen zu erkennen.

Abb. 9: Drittelpunkte
Fr ein beliebiges Teilverhltnis t wird aus (4) die Bedingung:
![]() (5)
(5)
Fr t = 0 ergibt sich aus (5) das regelm§ige n-Eck, fr t = 1 das regelm§ige n–1-Eck.
Durch Variation von t zwischen 0 und 1 knnen wir also ein n-Eck in ein n–1-Eck verwandeln.
Die folgenden Animationen illustrieren den Sachverhalt.
Animation 1: Dreieck und Viereck

Animation 2: Viereck und Fnfeck

Animation 3: Fnfeck und Sechseck
Websites
Hans Walser: Logarithmische Kantenmittenspiralen
www.walser-h-m.ch/hans/Miniaturen/L/Log_Kantenmittenspiralen/Log_Kantenmittenspiralen.htm
Hans Walser: Spiralen im regelm§igen Vieleck
www.walser-h-m.ch/hans/Miniaturen/S/Spiralen_reg_Vieleck/Spiralen_reg_Vieleck.htm
Hans Walser: Kantenmittenspirale
www.walser-h-m.ch/hans/Miniaturen/K/Kantenmittenspirale/Kantenmittenspirale.htm