Hans Walser, [20200714]
Logarithmische Kantenmittenspiralen
Anregung: M. E., B.
1 Worum geht es?
Logarithmische Kantenmittenspiralen, welche sich in zyklischer Folge ein- und umbeschrieben sind.
2 Einstiegsbeispiel
Wir beginnen mit einem regelmŠ§igen Achteck (Abb. 1.1a). Jede zweite Kante ist farbig angemalt, im positiven Drehsinn in den Farben rot, gelbgrźn, hellblau und violett.
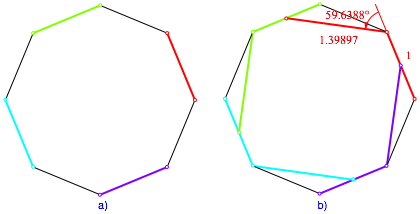
Abb. 1.1: Start und erster Schritt
Nun verbinden wir das im positiven Drehsinn zweite Ende der roten Startstrecke mit dem Mittelpunkt der gelbgrźnen Strecke (Abb. 1.1b). Diese Verbindung zeichnen wir rot. Sie ist deutlich lŠnger (139.897%) als die rote Startstrecke. Analog verbinden wir das Ende der gelbgrźnen Startstrecke mit dem Mittelpunkt der hellblauen Strecke. Ebenso verfahren wir mit hellblau und violett.
Die Abbildung 1.2 zeigt die beiden nŠchsten Schritte. Wir sehen, dass die LŠngen der neuen Strecken keinem erkennbaren Muster folgen. Auch die Winkel zwischen aufeinanderfolgenden Strecken gleicher Farbe variieren.
Aus Symmetriegrźnden sind die Spiralen der verschiedenen Farben kongruent.

Abb. 1.2: Schritte drei und vier
In der Abbildung 1.3 sehen wir zwei weitere Schritte.
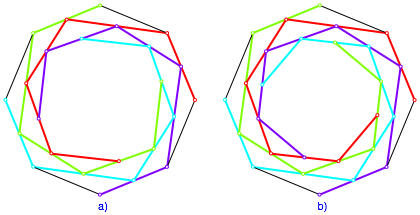
Abb. 1.3: Weitere Schritte
Die Tabelle 1 gibt fźr eine Spirale (die rote) die LŠngen-VerŠnderungsfaktoren zweier aufeinanderfolgender Strecken sowie deren RichtungsŠnderung (Au§enwinkel).
Lesebeispiel: Beim †bergang vom der ersten zur zweiten Strecke haben wir einen LŠngen-VerŠnderungsfaktor 1.398966326. Die zweite Strecke misst also etwa 139.897% der ersten. Sie weicht um einen Winkel von 59.63880658ˇ im positiven Drehsinn von der ersten ab. In der Abbildung 1.1b sind diese Daten eingetragen.
|
Schritt |
VerŠnderungsfaktor |
RichtungsŠnderung [ˇ] |
|
2 |
1.398966326 |
59.63880658 |
|
3 |
0.7472553970 |
65.62558310 |
|
4 |
0.9868422493 |
51.85877233 |
|
5 |
0.9053338153 |
63.88612868 |
|
6 |
0.8933681725 |
56.28259906 |
|
7 |
0.9348357449 |
60.13327190 |
|
8 |
0.8957770916 |
58.81640314 |
|
9 |
0.9222644246 |
58.81688762 |
|
10 |
0.9080905470 |
59.28576014 |
|
11 |
0.9134508382 |
58.78697287 |
|
12 |
0.9128420468 |
59.14692518 |
|
13 |
0.9115486769 |
58.94540429 |
|
14 |
0.9131407453 |
59.02933253 |
|
15 |
0.9119194226 |
59.01302936 |
|
16 |
0.9126400202 |
59.00003050 |
|
17 |
0.9123162402 |
59.01969206 |
|
18 |
0.9123995417 |
59.00353121 |
|
19 |
0.9124279882 |
59.01357631 |
|
20 |
0.9123677718 |
59.00875429 |
Tab. 1: VerŠnderungsfaktoren und RichtungsŠnderungen
Sowohl die LŠngen-VerŠnderungsfaktoren als auch die RichtungsŠderungen variieren am Anfang recht stark. Wir vermuten aber, dass sich diese Daten bei zunehmenden Schrittzahlen je einem Grenzwert annŠhern.
Die Abbildung 2 zeigt stark vergrš§ert den Ausschnitt fźr die Schrittzahlen von 15-20. Die Spiralen sehen aus wie logarithmische Spiralen mit konstantem LŠngen-VerŠnderungsfaktor und konstanter RichtungsŠnderung.

Abb. 2: Schritte 15-20
3 Berechnung der Grenzwerte
Wir gehen von vier logarithmischen Kantenmittenspiralen aus und betten diese in die Gau§sche Ebene der komplexen Zahlen ein (Abb. 3).
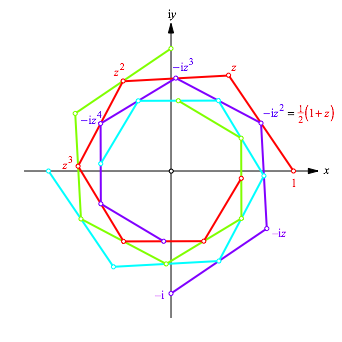
Abb. 3: Arbeitsfigur
Die Schlźsselzahl ist die Zahl z. Ihr Betrag ist der gesuchte konstante LŠngen-VerŠnderungsfaktor, ihr Argument die gesuchte konstante RichtungsŠnderung. Aus der Arbeitsfigur (Abb. 3) lesen wir fźr z die Bedingung ab:
![]() (1)
(1)
Diese quadratische Gleichung mit komplexen Koeffizienten hat fźr z die beiden Lšsungen:
 (2)
(2)
Man beachte, dass die beiden Lšsungen nicht konjugiert komplex sind, da die quadratische Gleichung (1) komplexe Koeffizienten enthŠlt.
Die fźr uns relevante erste Lšsung hat den Betrag
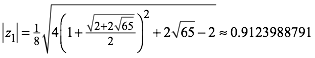 (3)
(3)
und das Argument:
![]() (4)
(4)
Diese Daten passen zu unseren Vermutungen auf Grund der Tabelle 1.
Die Abbildung 4 zeigt die vier zugehšrigen logarithmischen Kantenmittenspiralen.

Abb. 4: Logarithmische Kantenmittenspiralen
4 Allgemein
Fźr n Spiralen fźhrt die analoge †berlegung fźr die Schlźsselzahl z zur Bedingung:
![]() (5)
(5)
Diese quadratische Gleichung hat die beiden Lšsungen:
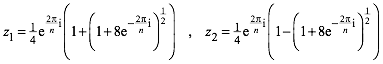 (6)
(6)
Die Tabelle 2 gibt die ersten BetrŠge (LŠngen-VerŠnderungsfaktoren) und die
relevanten RichtungsŠnderungen.
|
Anzahl Spiralen |
VerŠnderungsfaktor |
RichtungsŠnderung [ˇ] |
|
2 |
0.7071067812 |
110.7048111 |
|
3 |
0.8502352679 |
77.52110310 |
|
4 |
0.9123988791 |
59.01008801 |
|
5 |
0.9430182565 |
47.50705136 |
|
6 |
0.9600982308 |
39.71914504 |
|
7 |
0.9705414372 |
34.11053230 |
|
8 |
0.9773758771 |
29.88337441 |
|
9 |
0.9820866862 |
26.58510972 |
|
10 |
0.9854686738 |
23.94072904 |
Tab. 1: VerŠnderungsfaktoren und RichtungsŠnderung
5 Beispiele
Eine Bildergalerie
5.1 Zwei Spiralen
Der
VerŠnderungsfaktor ist ![]() , die RichtungsŠnderung:
, die RichtungsŠnderung:
![]() (7)
(7)
Die Abbildung 5 zeigt die beiden Spiralen.
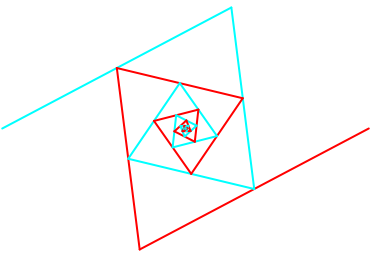
Abb. 5: Zwei Spiralen
Die Figur
ist aus gleichschenkligen Dreiecken mit der Basis 1 und den Schenkeln ![]() aufgebaut
(Abb. 6).
aufgebaut
(Abb. 6).

Abb. 6: Aufbau aus gleichschenkligen Dreiecken
5.2 Drei Spiralen
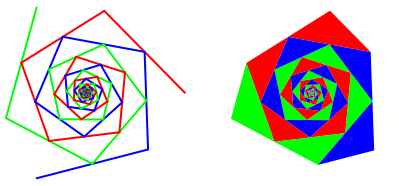
Abb. 7: Drei Spiralen
Die Dreiecke sind jetzt nicht mehr gleichschenklig.
5.3 Vier Spiralen

Abb. 8: Vier Spiralen
5.4 Fźnf Spiralen

Abb. 9: Fźnf Spiralen
5.5 Sechs Spiralen

Abb. 10: Sechs Spiralen
Websites
Hans Walser: Spiralen im regelmŠ§igen Vieleck
www.walser-h-m.ch/hans/Miniaturen/S/Spiralen_reg_Vieleck/Spiralen_reg_Vieleck.htm
Hans Walser: Kantenmittenspirale
www.walser-h-m.ch/hans/Miniaturen/K/Kantenmittenspirale/Kantenmittenspirale.htm