Hans Walser, [20201030]

Lotschnittpunkt

1 Worum geht es?

Spielerei mit Normalen einer archimedischen Spirale. Schnittpunkt

2 Konstruktion

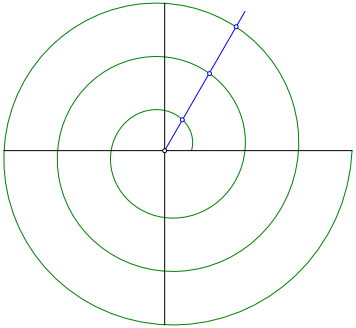
Abb.1: Archimedische Spirale

Zu einer archimedischen Spirale mit der Polardarstellung

(1)

zeichnen wir einen vom Ursprung ausgehenden Strahl (blau in Abb. 1).

In jedem Schnittpunkt des Strahls mit der archimedischen Spirale zeichnen wir das Lot zur Spirale (Kurvennormale, rot in Abb. 2).

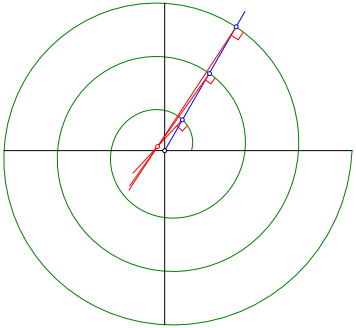
Abb.2: Spiralenlote

Diese Spiralenlote schneiden sich in einem Punkt.

Dieser Schnittpunkt liegt auch auf dem Lot des eingangs gezeichneten Strahls (Abb. 3).

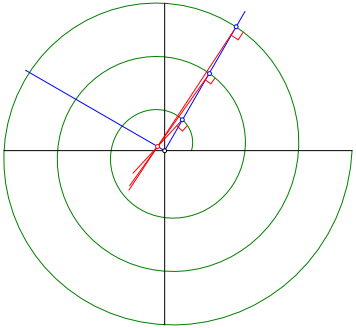
Abb. 3: Schnittpunkt auf blauem Lot

Weiter liegt der Schnittpunkt auf dem Kreis um den Ursprung mit dem Radius a (Abb. 4).

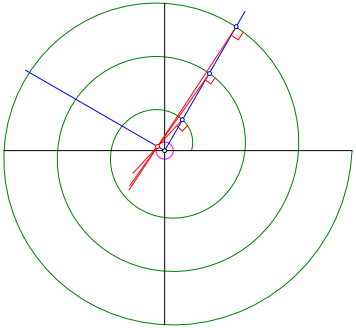
Abb. 4: Schnittpunkt auf Kreis

Der Umfang dieses Kreises ist der Radialzuwachs der archimedischen Spirale bei einem Umlauf.

3 Beweise

Beweise rechnerisch.

Bemerkung: Der Schnittpunkt liegt nicht auf der Evolute der archimedischen Spirale. Die Evolute der archimedischen Spirale ist ihrerseits eine Spirale. Sie hat den Kreis als Asymptote.

Weblinks

Hans Walser: Schnittpunkte 801-900. Schnittpunkte 826 und 827

http://www.walser-h-m.ch/hans/Schnittpunkte/Schnittpunkte_801-900.htm