Hans Walser, [20171023]

Magische Quadrate überlagern

1 Worum geht es?

Es werden magische Quadrate verschiedener ungerader Seitenlängen überlagert. Vorgehen exemplarisch mit den Seitenlänge 3 und 5.

2 Fünf mal drei

2.1 Seitenlänge 3

Die Abbildung 1 zeigt ein magisches Quadrat der Seitenlänge 3. Die Zahlen laufen von 0 bis 8. Das magische Quadrat wurde nach dem in [1] geschilderten Verfahren hergestellt.

5	6	1
0	4	8
7	2	3

Abb. 1: Magisches Quadrat der Seitenlänge 3

Die Abbildung 2 zeigt das zugehörige Histogramm. Es ist mit dem Faktor unterhöht gezeichnet.

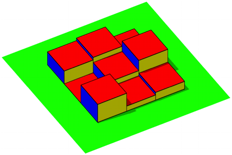
Abb. 2: Histogramm

Die Abbildung 3 zeigt dieses magische Quadrat in 25 Exemplaren extended. Es handelt sich natürlich immer noch um ein magisches Quadrat. Die Zahlen laufen mehrfach von 0 bis 8.

5	6	1	5	6	1	5	6	1	5	6	1	5	6	1
0	4	8	0	4	8	0	4	8	0	4	8	0	4	8
7	2	3	7	2	3	7	2	3	7	2	3	7	2	3
5	6	1	5	6	1	5	6	1	5	6	1	5	6	1
0	4	8	0	4	8	0	4	8	0	4	8	0	4	8
7	2	3	7	2	3	7	2	3	7	2	3	7	2	3
5	6	1	5	6	1	5	6	1	5	6	1	5	6	1
0	4	8	0	4	8	0	4	8	0	4	8	0	4	8
7	2	3	7	2	3	7	2	3	7	2	3	7	2	3
5	6	1	5	6	1	5	6	1	5	6	1	5	6	1
0	4	8	0	4	8	0	4	8	0	4	8	0	4	8
7	2	3	7	2	3	7	2	3	7	2	3	7	2	3
5	6	1	5	6	1	5	6	1	5	6	1	5	6	1
0	4	8	0	4	8	0	4	8	0	4	8	0	4	8
7	2	3	7	2	3	7	2	3	7	2	3	7	2	3

Abb. 3: Magisches Quadrat der Seitenlänge 15

Die Abbildung 4 zeigt das zugehörige Histogramm.

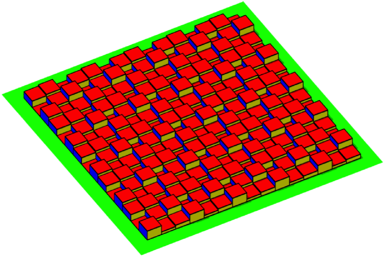
Abb. 4: Niedlich

2.2 Seitenlänge 5

Die Abbildung 5 zeigt ein magisches Quadrat der Seitenlänge 5. Die Zahlen laufen von 0 bis 24. Das magische Quadrat wurde nach dem in [1] geschilderten Verfahren hergestellt.

13	19	20	1	7
9	10	16	22	3
0	6	12	18	24
21	2	8	14	15
17	23	4	5	11

Abb. 5: Magisches Quadrat der Seitenlänge 5

Die Abbildung 6 zeigt das zugehörige Histogramm.

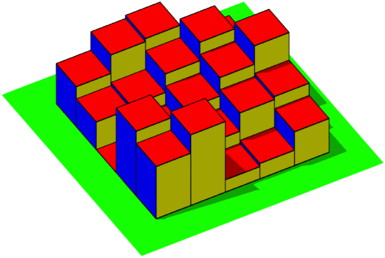
Abb. 6: Histogramm

Die Abbildung 7 zeigt 25 Felder der Seitenlänge 3, in denen sich lauter gleiche Zahlen befinden. Diese sind das 9-fache der Zahlen in entsprechender Lage in der Abbildung 5.

117	117	117	171	171	171	180	180	180	9	9	9	63	63	63
117	117	117	171	171	171	180	180	180	9	9	9	63	63	63
117	117	117	171	171	171	180	180	180	9	9	9	63	63	63
81	81	81	90	90	90	144	144	144	198	198	198	27	27	27
81	81	81	90	90	90	144	144	144	198	198	198	27	27	27
81	81	81	90	90	90	144	144	144	198	198	198	27	27	27
0	0	0	54	54	54	108	108	108	162	162	162	216	216	216
0	0	0	54	54	54	108	108	108	162	162	162	216	216	216
0	0	0	54	54	54	108	108	108	162	162	162	216	216	216
189	189	189	18	18	18	72	72	72	126	126	126	135	135	135
189	189	189	18	18	18	72	72	72	126	126	126	135	135	135
189	189	189	18	18	18	72	72	72	126	126	126	135	135	135
153	153	153	207	207	207	36	36	36	45	45	45	99	99	99
153	153	153	207	207	207	36	36	36	45	45	45	99	99	99
153	153	153	207	207	207	36	36	36	45	45	45	99	99	99

Abbildung 7: Aufgeblasene Abbildung 5

Die Abbildung 8 zeigt das zugehörige Histogramm. Wir sehen Plateaus.

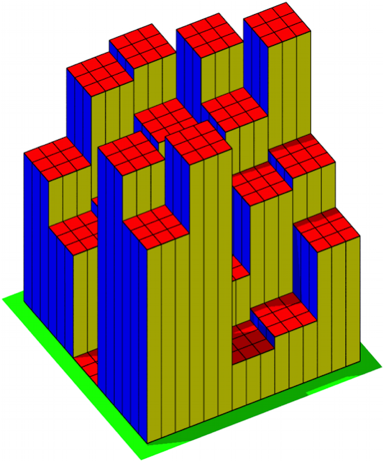
Abb. 8: Histogramm

2.3 Überlagerung

Nun setzen wir auf jedes der 25 Felder mit gleichen Zahlen das magische Quadrat der Abbildung 1 auf. Anders gesagt: wir addieren die magischen Quadrate der Abbildungen 3 und 7. Dies gibt das magische Quadrat der Abbildung 9.

122	123	118	176	177	172	185	186	181	14	15	10	68	69	64
117	121	125	171	175	179	180	184	188	9	13	17	63	67	71
124	119	120	178	173	174	187	182	183	16	11	12	70	65	66
86	87	82	95	96	91	149	150	145	203	204	199	32	33	28
81	85	89	90	94	98	144	148	152	198	202	206	27	31	35
88	83	84	97	92	93	151	146	147	205	200	201	34	29	30
5	6	1	59	60	55	113	114	109	167	168	163	221	222	217
0	4	8	54	58	62	108	112	116	162	166	170	216	220	224
7	2	3	61	56	57	115	110	111	169	164	165	223	218	219
194	195	190	23	24	19	77	78	73	131	132	127	140	141	136
189	193	197	18	22	26	72	76	80	126	130	134	135	139	143
196	191	192	25	20	21	79	74	75	133	128	129	142	137	138
158	159	154	212	213	208	41	42	37	50	51	46	104	105	100
153	157	161	207	211	215	36	40	44	45	49	53	99	103	107
160	155	156	214	209	210	43	38	39	52	47	48	106	101	102

Abb. 9: Magisches Quadrat

Die Abbildung 10 zeigt das zugehörige Histogramm. Es ist die Überlagerung der beiden Histogramme der Abbildungen 4 und 8.

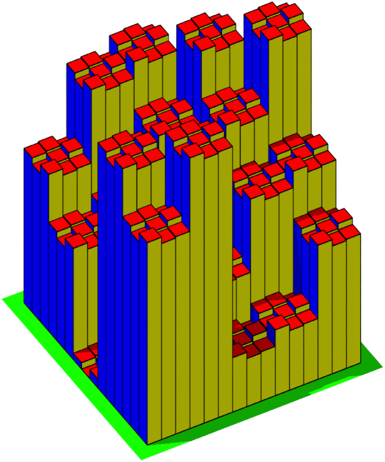
Abb. 10: Histogramm

2.4 Symmetrien

Im magischen Quadrat der Abbildung 9 können Symmetrien sichtbar gemacht werden. In der Abbildung 11 sind alle geraden Zahlen gelb unterlegt.

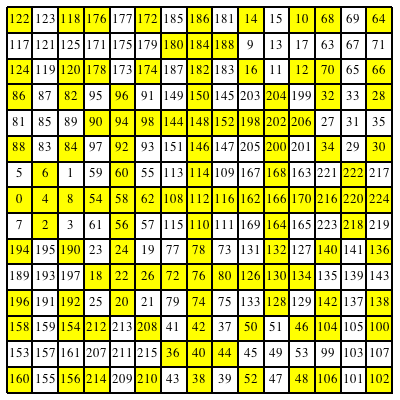
Abb. 11: Gerade Zahlen

In der Abbildung 12 sind alle durch drei teilbare Zahlen gelb unterlegt.

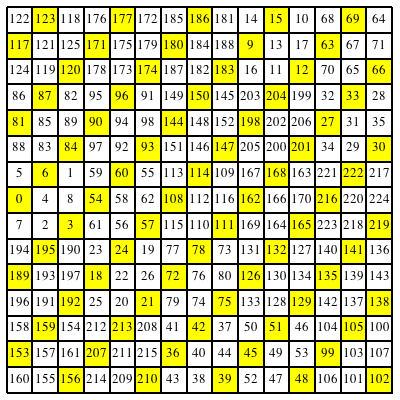
Abb. 12: Vielfache von 3

In der Abbildung 13 sind die Vielfachen von 9 gelb unterlegt.

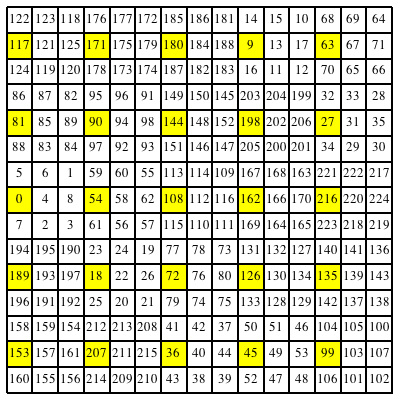
Abb. 13: Vielfache von 9

Wenn wir die gelb unterlegten Zahlen herausgreifen und durch 9 dividieren, erhalten wir das magische Quadrat der Abbildung 5.

3 Drei mal fünf

3.1 Das magische Quadrat

Wir vertauschen gegenüber dem vorhergehenden Abschnitt die Rollen der beiden Zahlen drei und fünf. Dies führt zum magischen Quadrat der Abbildung 14.

138	144	145	126	132	163	169	170	151	157	38	44	45	26	32
134	135	141	147	128	159	160	166	172	153	34	35	41	47	28
125	131	137	143	149	150	156	162	168	174	25	31	37	43	49
146	127	133	139	140	171	152	158	164	165	46	27	33	39	40
142	148	129	130	136	167	173	154	155	161	42	48	29	30	36
13	19	20	1	7	113	119	120	101	107	213	219	220	201	207
9	10	16	22	3	109	110	116	122	103	209	210	216	222	203
0	6	12	18	24	100	106	112	118	124	200	206	212	218	224
21	2	8	14	15	121	102	108	114	115	221	202	208	214	215
17	23	4	5	11	117	123	104	105	111	217	223	204	205	211
188	194	195	176	182	63	69	70	51	57	88	94	95	76	82
184	185	191	197	178	59	60	66	72	53	84	85	91	97	78
175	181	187	193	199	50	56	62	68	74	75	81	87	93	99
196	177	183	189	190	71	52	58	64	65	96	77	83	89	90
192	198	179	180	186	67	73	54	55	61	92	98	79	80	86

Abb. 14: Magisches Quadrat

Die Abbildung 15 zeigt das zugehörige Histogramm.

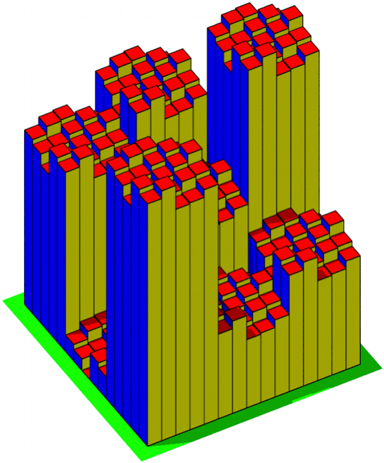
Abb. 15: Histogramm

3.2 Symmetrien

In der Abbildung 16 sind alle geraden Zahlen des magischen Quadrates der Abbildung 14 gelb unterlegt. Die Anordnungen unterscheiden sich gegenüber der Abbildung 11.

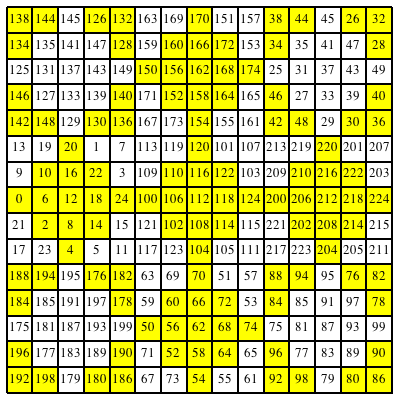
Abb. 16: Gerade Zahlen

In der Abbildung 17 sind alle durch drei teilbaren Zahlen gelb unterlegt. Wir erkennen ein Parkett. Die Anordnungen unterscheiden sich gegenüber der Abbildung 12.

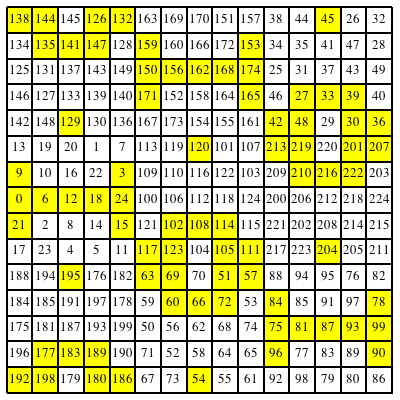
Abb. 17: Durch drei teilbare Zahlen

In der Abbildung 18 sind alle durch 25 teilbaren Zahlen gelb unterlegt.

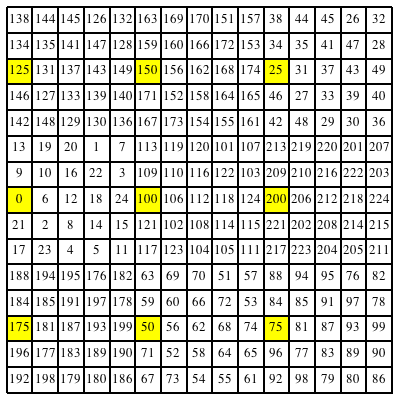
Abb. 18: Durch 25 teilbare Zahlen

Wenn wir diese Zahlen herausgreifen und durch 25 dividieren, erhalten wir das magische Quadrat der Abbildung 1.

3.3 Unterschiede

Die beiden magischen Quadrate der Abbildungen 9 und 14 unterscheiden sich. Unser Konstruktionsverfahren ist nicht kommutativ. Die Abbildung 19 zeigt das Differenzenquadrat.

–16	–21	–27	50	45	9	16	16	30	–143	–23	–34	23	43	32
–17	–14	–16	24	47	20	20	18	16	–144	–21	–18	22	20	43
–1	–12	–17	35	24	24	31	20	15	–158	–14	–19	33	22	17
–60	–40	–51	–44	–44	–80	–3	–8	–19	38	158	172	–1	–6	–12
–61	–63	–40	–40	–42	–69	–29	–6	–3	37	160	158	–2	1	–1
75	64	64	96	85	–20	32	26	46	98	–13	–18	–186	–172	–177
–4	–4	–15	37	57	–54	3	–2	–13	64	–41	–47	5	0	14
0	–2	–4	36	34	–38	2	0	–2	38	–34	–36	4	2	0
–14	0	–5	47	41	–64	13	2	–3	54	–57	–37	15	4	4
177	172	186	18	13	–98	–46	–26	–32	20	–85	–96	–64	–64	–75
1	–1	2	–158	–160	–37	3	6	29	69	42	40	40	63	61
12	6	1	–172	–158	–38	19	8	3	80	44	44	51	40	60
–17	–22	–33	19	14	158	–15	–20	–31	–24	–24	–35	17	12	1
–43	–20	–22	18	21	144	–16	–18	–20	–20	–47	–24	16	14	17
–32	–43	–23	34	23	143	–30	–16	–16	–9	–45	–50	27	21	16

Abb. 19: Differenzenquadrat

Das Differenzenquadrat ist antipunktsymmetrisch. Punktsymmetrisch zum Zentrum gelegene Zahlen sind entgegengesetzt gleich.

4 Direkte Konstruktion eines magischen Quadrates

4.1 Das magische Quadrat

Die Abbildung 20 zeigt ein magisches Quadrat der Seitenlänge 15, das direkt nach dem in [1] geschilderten Verfahren hergestellt wurde.

113	129	145	161	177	193	209	210	1	17	33	49	65	81	97
99	115	131	147	163	179	180	196	212	3	19	35	51	67	83
85	101	117	133	149	150	166	182	198	214	5	21	37	53	69
71	87	103	119	120	136	152	168	184	200	216	7	23	39	55
57	73	89	90	106	122	138	154	170	186	202	218	9	25	41
43	59	60	76	92	108	124	140	156	172	188	204	220	11	27
29	30	46	62	78	94	110	126	142	158	174	190	206	222	13
0	16	32	48	64	80	96	112	128	144	160	176	192	208	224
211	2	18	34	50	66	82	98	114	130	146	162	178	194	195
197	213	4	20	36	52	68	84	100	116	132	148	164	165	181
183	199	215	6	22	38	54	70	86	102	118	134	135	151	167
169	185	201	217	8	24	40	56	72	88	104	105	121	137	153
155	171	187	203	219	10	26	42	58	74	75	91	107	123	139
141	157	173	189	205	221	12	28	44	45	61	77	93	109	125
127	143	159	175	191	207	223	14	15	31	47	63	79	95	111

Abb. 20: Magisches Quadrat der Seitenlänge 15

Es unterscheidet sich von den magischen Quadraten der Abbildungen 9 und 14.

4.2 Histogramm

Die Abbildung 21 zeigt das zugehörige Histogramm.

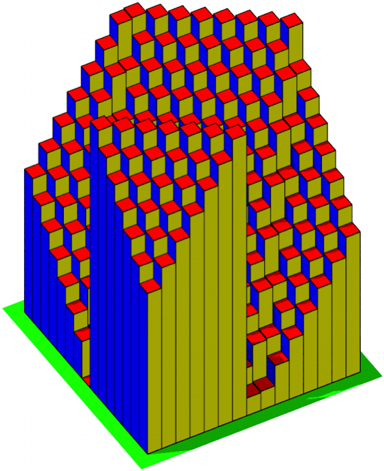
Abb. 21: Histogramm

Die Abbildung 22 zeigt eine andere Sicht auf dasselbe Histogramm.

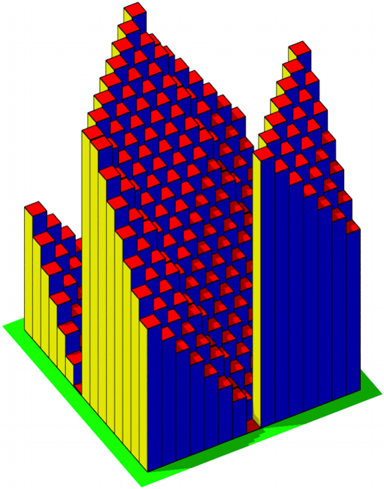
Abb. 22: Wo Berge sich erheben

4.3 Symmetrien

Die Symmetrien sind nochmals anders.

In der Abbildung 23 sind die geraden Zahlen des magischen Quadrates der Abbildung 20 gelb unterlegt.

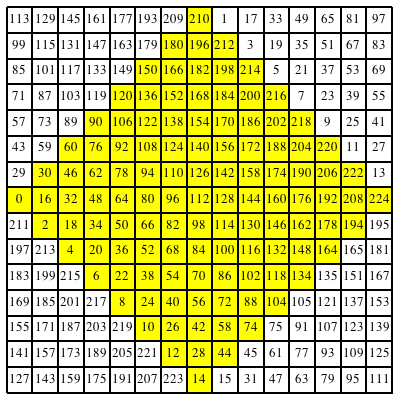
Abb. 23: Gerade Zahlen

In der Abbildung 24 sind die durch drei teilbaren Zahlen gelb unterlegt. Dieses Muster hatten wir schon in der Abbildung 12.

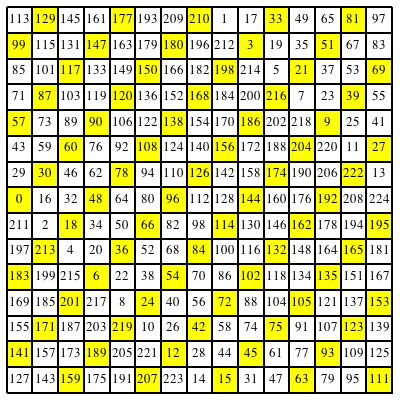
Abb. 24: Durch drei teilbare Zahlen

In der Abbildung 24 sind die durch sieben teilbaren Zahlen gelb unterlegt.

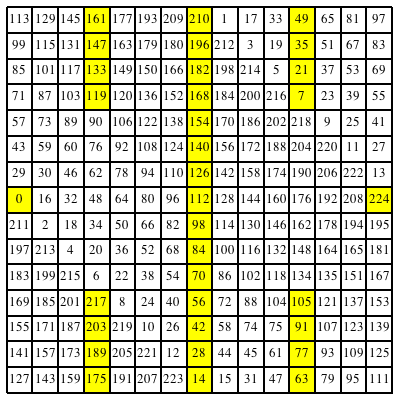
Abb. 25: Durch sieben teilbare Zahlen

Websites

[1] Hans Walser: Magische Quadrate ungerader Seitenlänge (23.10.2017):

www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate/Mag_Quadrate.htm

[2] Hans Walser: Magische Quadrate quadrieren (23.10.2017):

www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate2/Mag_Quadrate2.htm