Hans Walser, [20200425]
Magische Quadrate
Idee und Anregung: Thomas Jahre, Chemnitz, Aufgabe der Woche
Serie 54 – Aufgabe 3 - Problem 639
1 Worum geht es?
Magische Quadrate der SeitenlŠnge 3.
2 Problemstellung
ăMit den Zahlen 1, 2, É , 9 lŠsst sich ja schnell ein magisches Quadrat erstellenŇ, sagte Mike zu Bernd. ăKlar, wenn man von Spiegelung und Drehung absieht, gibt es aber auch nur einsŇ, erwiderte Bernd.
(1) Zu zeigen ist, dass bei der Multiplikation jeder Zahl des gefundenen Quadrates mit der selben ganzen Zahl g das so entstehende Quadrat auch magisch ist.
(2)
Ist es mšglich aus den Brźchen ![]() auch ein magisches Quadrat zu erstellen?
auch ein magisches Quadrat zu erstellen?
(3)
Gibt es ein magisches Quadrat, welches
nur Stammbrźche - also von der Form ![]() –
aufweist?
–
aufweist?
3 Bearbeitung
3.1 Beispiel
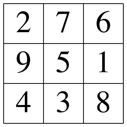
Abb. 1: Beispiel
Die magische Summe (Zeilen-, Spalten- und Diagonalensumme) ist 15.
3.2 Formal
Wir kšnnen ein magisches Quadrat der SeitenlŠnge 3 generieren wie folgt.
In der ersten Zeile kšnnen wir drei beliebige Zahlen x, y, z wŠhlen. Die źbrigen Felder fźllen wir gemŠ§ Abbildung 2 aus.
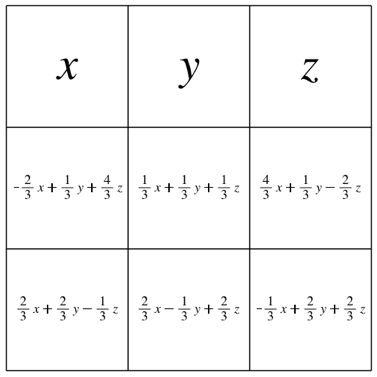
Abb. 2: Formales Vorgehen
Die magische Summe ist x + y + z.
Im zentralen Feld steht ein Drittel der magischen Summe. Das ist auch ein Neuntel der Gesamtsumme aller vorkommenden Zahlen.
3.3 Vektorraum
Da die Formeln linear sind, ist eine Linearkombination zweier magischer Quadrate wieder ein magisches Quadrat. Wir haben einen Vektorraum. Damit ist (1) gezeigt.
Das Neutralelement des Vektorraums ist das magische Quadrat, welches aus lauter Nullen besteht.
Da wir drei freie Parameter haben, hat der Vektorraum die Dimension 3. Die Abbildung 3 zeigt eine Basis dieses Vektorraums.
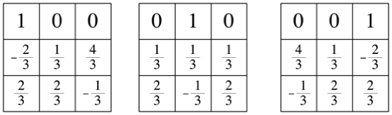
Abb. 3: Basis des Vektorraums
Zu jedem Punkt des euklidischen Raumes gehšrt genau ein magisches Quadrat und umgekehrt. Wir kšnnen die drei Zahlen in der ersten Zeile als kartesische Raumkoordinaten deuten.
3.4 Drehen und Spiegeln
Die Abbildung 4 zeigt die magischen Quadrate, die sich aus dem Beispiel der Abbildung 1 durch Drehen und Spiegeln ergeben.
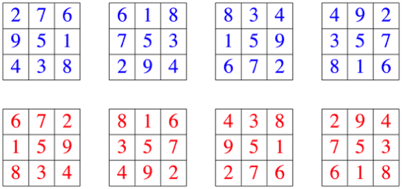
Abb. 4: Drehen und Spiegeln
Die zugehšrigen Punkte im euklidischen Raum ergeben sich durch die jeweils erste Zeile. Die Punkte liegen alle auf der Ebene x + y + z = 15 (magische Summe). In einer geeigneten isometrischen Darstellung sehen wir diese Ebene unverzerrt (Abb. 5).
Die vier blauen und die vier roten Punkte bilden zwei spiegelbildliche Parallelogramme.
Weiter sehen wir zwei Rechtecke. Das eine ist doppelt so breit aber nur halb so lang wie das andere. Die beiden Rechtecke haben daher den gleichen FlŠcheninhalt.
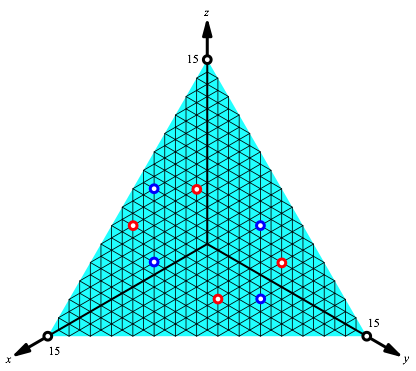
Abb. 5: Die acht magischen Quadrate
3.5 Kehrwerte
Aus den
Brźchen ![]() lŠsst sich
kein magisches Quadrat bauen.
lŠsst sich
kein magisches Quadrat bauen.
Begrźndung: Die Zahl im zentralen Feld wŠre:
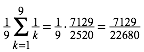 (1)
(1)
Dies ist
kein Element aus ![]() . Damit ist (2) widerlegt.
. Damit ist (2) widerlegt.
Wenn wir
die Zahlen des Beispiels der Abbildung 1 dividieren durch das kleinste gemeinsame
Vielfache dieser Zahlen, erhalten wir das magische Quadrat der Abbildung 6. Es
besteht aus lauter Stammbrźchen. Die magische Summe ist ![]() , also ebenfalls ein Stammbruch.
, also ebenfalls ein Stammbruch.
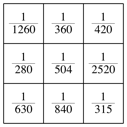
Abb. 6: Magisches Quadrat aus Stammbrźchen.
3.6 Standardisierung
Die Abbildung 7 zeigt ein magisches Quadrat mit den ganzen Zahlen –4, –3, ... , 3, 4. Es entsteht aus dem magischen Quadrat der Abbildung 1 durch Subtraktion von 5.
Die magische Summe ist null.
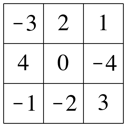
Abb. 7: Standardisierte Version
Symmetrien sind offensichtlich.
3.7 Magisches Produkt
Die Abbildung 8 zeigt ein Quadrat, bei dem die Zeilen-, Spalten- und Diagonalenprodukte gleich 1 sind (magisches Produkt).
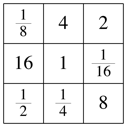
Abb. 8: Magisches Produkt
Websites
Thomas Jahre, Aufgabe der Woche, Serie 54, Problem 639
www.schulmodell.eu/unterricht/faecher/mathematik/wochenaufgabe/serie-54.html
Hans Walser: Magische Kreise
http://www.walser-h-m.ch/hans/Miniaturen/M/Magische_Kreise/Magische_Kreise.htm
Hans Walser: Magische Puzzle
http://www.walser-h-m.ch/hans/Miniaturen/M/Mag_Puzzle/Mag_Puzzle.htm
Hans Walser: Magische Quadrate ungerader SeitenlŠnge
http://www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate/Mag_Quadrate.htm
Hans Walser: Magische Quadrate źberlagern
http://www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate4/Mag_Quadrate4.htm
Hans Walser: Magische Quadrate źberlagern
http://www.walser-h-m.ch/hans/Miniaturen/M/Mag_Quadrate2/Mag_Quadrate2.htm
Hans Walser: Magisches Fraktal
www.walser-h-m.ch/hans/Miniaturen/M/Magisches_Fraktal/Magisches_Fraktal.htm
Hans Walser: Vortrag: Magische Symmetrie
http://www.walser-h-m.ch/hans/Vortraege/20181117/index.html
Literatur
Walser, Hans (2018): Magische
Symmetrie. MI, Mathematikinformation Nr. 69, 15. September 2018. ISSN
1612-9156. 25-33.