Hans Walser, [20131223]
Matterhorn
1 Worum geht es?
Es wird ein Bauteil vorgestellt, mit dem sich die Ebene parkettieren lŠsst. Insbesondere kšnnen auch spiralfšrmige Parkette ausgelegt werden. Es gibt eine reichhaltige Literatur darźber.
2 Der Parkettstein
Wir beginnen mit einem regelmŠ§igen Vieleck mit 6n, n = 2, 3, 4, 5, ..., Ecken und zerlegen es in Sektoren gemŠ§ Abbildung 1. Der Faktor 6 in der Eckenzahl garantiert die Existenz einer Diagonale gleicher LŠnge wie der Umkreisradius.
Die Abbildung 1 zeigt die Situation fźr n = 2, 3 und 4.

Abb. 1: Sektoren
Die beiden Sektorengrenzen sind jeweils kongruent zu n aufeinander folgenden Kanten des regelmŠ§igen Vieleckes. Ein einzelner Sektor ist unser Parkettstein.
Wir beschrŠnken uns in unserer Studie auf den Fall n = 2, also einen Sektor im regelmŠ§igen Zwšlfeck. Die Abbildung 2 zeigt die Winkel dieses Parkettsteins.
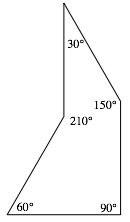
Abb. 2: Winkel
Der Parkettstein erinnert an das Matterhorn (Abb. 3):
Abb. 3: Matterhorn
Wir werden den Parkettstein auch in seiner spiegelbildlichen Form verwenden, ebenso gelegentlich mit kreisfšrmigen Randlinien (Abb. 4). Die Radien der Begrenzungsbšgen sind gleich dem Umkreisradius des ursprźnglichen Zwšlfecks.
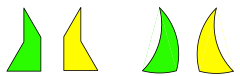
Abb. 4: Bausteine
3 Beispiele
3.1 Zwšlfeck und Kreis
Das Zwšlfeck und Kreis kšnnen auf verschiedene Arten zusammengesetzt werden.
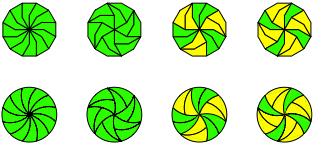
Abb. 5: Zwšlfeck und Kreis
3.2 BŠnder
Die Abbildung 6 zeigt BŠnder vom gleichen Typus, aber mit unterschiedlichen Gestaltungen der Knickstelle. Der gerade Teil der BŠnder hat eine Schubspiegelsymmetrie.

Abb. 6: BŠnder
Die Abbildung 7 zeigt einen anderen Typus.

Abb. 7: Andere BŠnder
Bei den glattrandigen Beispielen der Abbildung 7 unterliegen wir einer optischen TŠuschung, indem es scheint, dass die BŠnder gegen links breiter werden. Die Abbildung 8 illustriert dieselbe optische TŠuschung.

Abb. 8: Sind die roten Linien parallel?
Der TŠuschungseffekt entsteht dadurch, dass wir bestrebt sind, die Trajektorien durch die schrŠgen Richtungsfelder als Orthogonal-Trajektorien zu sehen. Viele optische TŠuschungen arbeiten mit diesem Prinzip.
Die Abbildung 9 zeigt ein weiteres Band. Es hat keine Schubspiegelsymmetrie wie die BŠnder der Abbildungen 6 und 7, hingegen eine Punktspiegelsymmetrie.
![]()
Abb. 9: Punktspiegelsymmetrie
Es ist mir nicht gelungen, dieses Band elegant abzuknicken. Auch lŠsst sich dieses Band nicht mit krummlinigen Parkettsteinen auslegen.
3.3 Ringe
Wir kšnnen aus den glattrandigen BŠndern der Abbildungen 6 oder 7 durch geeignetes Abknicken Zwšlfecke herstellen, die ein gegebenes zentrales Zwšlfeck umfassen. Die Abbildung 10 zeigt ein Beispiel.

Abb. 10: Ringe um das Zwšlfeck
3.4 Spiralen
Die Spiralen entstehen, indem wir die glattrandigen BŠnder der Abbildungen 6 oder 7 mit geeigneten Knickstellen ăaufwickelnŇ. Es sind daher eckige archimedische Spiralen. †ber Spiralen siehe [Heitzer 1998]. Im Folgenden einige Beispiele.
Das Interessanteste beim Bau dieser Spiralen ist der Start im Zentrum.
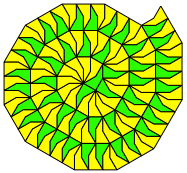
Abb. 11: Eckige archimedische Spirale

Abb. 12: Spirale mit zwei Armen
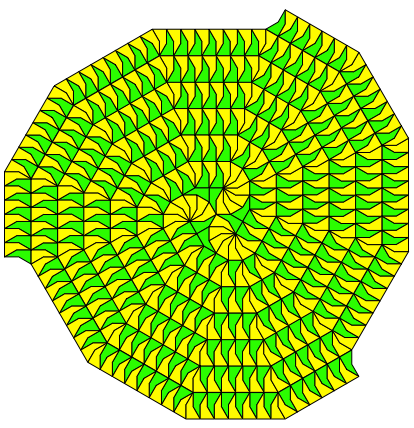
Abb. 13: Spirale mit drei Armen

Abb. 14: Spirale mit vier Armen
Fźr eine Spirale mit fźnf Armen mźssten wir mit dem Bauteil aus einem 30-Eck arbeiten.

Abb. 15: Spirale mit sechs Armen

Abb. 16: Spirale mit zwšlf Armen
4 Der Parkettstein und das Quadrat
Wir umschreiben dem Parkettstein ein Quadrat gemŠ§ Abbildung 17a.

Abb. 17: Parkettstein und Quadrat
Der Parkettstein macht dann flŠchenmŠ§ig einen Viertel des Quadrates aus. Die Abbildung 17b gibt einen Tipp, um das ein zusehen.
Literatur
[Goldberg 1955] Goldberg,
Michael: Central Tesselations. Scripta Mathematica (21) 1955, p. 253-260
[Grźnbaum/Shephard 1979] Grźnbaum, Branko / G. c. Shephard: Spiral
Tilings and Versatiles. Mathematics Teaching. No. 88, September 1979, p. 50-51
[Grźnbaum/Shephard 1987] Grźnbaum,
Branko / Shephard, G. C.: Tilings and
Patterns. New York: Freeman 1987. ISBN 0-7167-1193-1
[Hatch 1978] Hatch,
Gillian: Tessellations with Equilateral Reflex Polygons. Mathematics Teaching
(84) 1978, p. 32
[Heitzer 1998] Heitzer, Johanna: Spiralen, ein Kapitel phŠnomenaler Mathematik. Leipzig: Klett 1998. ISBN 3-12-720044-7
[Lindgren 1972] Lindgren,
H.: Geometric Dissections. Revised and enlarged by Greg Frederickson. New York:
Dover 1972.
[Simonds 1977] Simonds,
David R.: Central Tessellations with an Equilateral Pentagon. Mathematics
Teaching (83) 1977, p. 36-37
[Simonds 1978] Simonds,
David R.: Untitled note. Mathematics Teaching (84) 1978, p. 33
[Vorderberg 1936] Vorderberg, Heinz: Zur Zerlegung der Umgebung eines ebenen Bereiches in kongruente. Jahresbericht der deutschen Mathematiker-Vereinigung, 46 (1936), S. 229-231
[Vorderberg 1937] Vorderberg, Heinz: Zur Zerlegung der Ebene in kongruente Bereiche in Form einer Spirale. Jahresbericht der deutschen Mathematiker-Vereinigung, 47 (1937), S. 159-160