Hans Walser, [20180601]

Maximales Rechteck

Anregung: Thomas Jahre, Chemnitz

1 Die Aufgabenstellung

Einem Dreieck soll ein Rechteck mit maximalem Flächeninhalt einbeschrieben werden.

2 Rechtwinkliges Dreieck

Einem rechtwinkligen Dreieck (Abb. 1) soll ein Rechteck maximaler Fläche einbeschrieben werden.

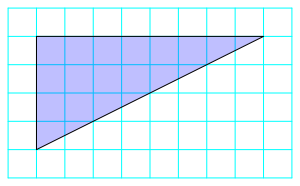
Abb. 1: Rechtwinkliges Dreieck

2.1 Die klassische Lösung

Die Abbildung 2 zeigt die klassische schulmäßige Lösung.

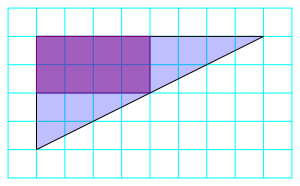
Abb. 2: Klassische Lösung

Diese Lösung orientiert sich am rechten Winkel.

2.2 Die schräge Lösung

Die Abbildung 3 zeigt eine weitere Lösung.

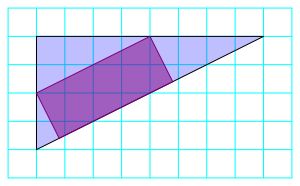
Abb. 3: Die schräge Lösung

2.3 Flächengleichheit

Die beiden Lösungen sind zwar nicht kongruent, aber zerlegungsgleich und damit flächengleich (Abb. 4). Die Zerlegung zeigt auch, dass die Rechteckfläche die Hälfte der Dreieckfläche ausmacht.

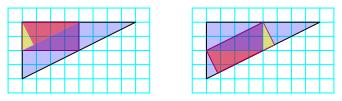
Abb. 4: Zerlegungsgleichheit

3 Spitzwinkliges Dreieck

Einem beliebigen spitzwinkligen Dreieck soll ist ein Rechteck mit maximalem Flächeninhalt einbeschrieben werden. Es gibt drei Lösungen (Abb. 5).

Abb. 5: Drei Lösungen

Die drei Lösungen sind nicht kongruent, aber zerlegungsgleich (Abb. 6) und damit flächengleich. Der Flächeninhalt ist die halbe Dreiecksfläche.

Abb. 6: Gemeinsame Zerlegung

4 Stumpfwinkliges Dreieck

Einem beliebigen stumpfwinkligen Dreieck soll ist ein Rechteck mit maximalem Flächeninhalt einbeschrieben werden. Es gibt nur eine Lösung (Abb. 7). Diese orientiert sich an der längsten Seite.

Abb. 7: Stumpfwinkliges Dreieck