Hans Walser, [20130705b]

Means, Pythagoras,  and Golden Section

Idea: M. N. D., N.

1        The Problem

Let p and q be two real numbers with  such that the arithmetic mean, the geometric mean and the harmonic mean of p and q are sides of a right triangle.

2        Solution

Since the arithmetic mean is the largest of the three means, we get by the theorem of Pythagoras:

 

We introduce the notation . In this notation we have:

,

 

or

,

 

or

,

 

or

.

 

Hence

.

 

Since  we have , where  (Golden Section, Walser 2001 and Walser 2013)).

Finally we get the condition .

 

3        Examples

3.1      The shape of the triangle

For  we have the three sides:

 

 

 

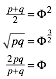
Figure 1 shows this example.

Fig. 1: The Right Golden Triangle

3.2      In the cardioid

The cardioid (Fig. 2) is a plane curve traced by a red point on the perimeter of the yellow circle (diameter 1) that is rolling around the fixed green circle of the same diameter.

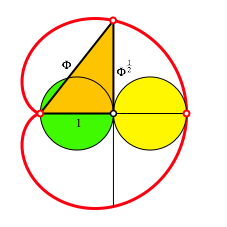
Fig. 2: In the cardioid

Inside the cardioid we find a Right Golden Triangle of the same shape (W1).

References

Walser, Hans (2001): The Golden Section. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America 2001. ISBN 0-88385-534-8.

Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Links

W1: http://www.walser-h-m.ch/hans/Miniaturen/K/Kardioide/Kardioide.htm