Hans Walser, [20180201]
Mehrfarbige Packungen
1 Worum geht es?
Die gngigen rumlichen Packungen werden bezglich der Minimalzahl der bentigten Farben untersucht. Wenn zwei Fller-Elemente eine Flche gemeinsam haben, verwenden wir zwei verschiedene Farben. Hingegen drfen zwei Fller-Elemente mit gemeinsamer Kante oder gemeinsamer Ecke dieselbe Farbe haben.
2 Kubische Packungen
Es handelt sich um das dreidimensionale ãSchachbrettÒ. Wir bentigen lediglich zwei Farben.
2.1 Mit Wrfeln
Wrfel mit gemeinsamer Seitenflche haben ungleiche Farben. Jeder Wrfel berhrt sechs konterfarbige Wrfel mit einer Seitenflche. Wrfel mit gemeinsamer Kante haben gleiche Farben. Wrfel mit gemeinsamer Ecke haben unterschiedliche Farben.
Die Abbildung 1 zeigt die Anordnung in einem gro§en Wrfel.

Abb. 1: Rumliches Schachbrett
Die Abbildung 2 zeigt die Anordnung in einer Pyramide. Die Seitenflchen der Pyramide haben gegenber der Grundflche einen Neigungswinkel 45¡.

Abb. 2: Als Pyramide
2.2 Mit Kugeln
Die Kugeln sind natrlich keine Raumfller. Sie lassen Zwischenrume offen. Sich berhrende Kugeln haben ungleiche Farben. Jede Kugel berhrt sechs konterfarbige Kugeln.
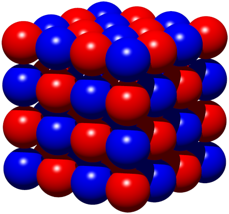
Abb. 3: Wrfelfrmige Anordnung
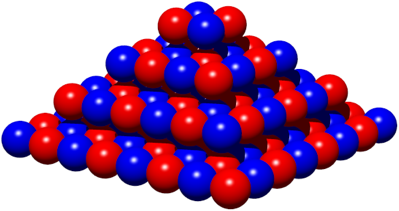
Abb. 4: Kugelpyramide
3 Kubisch raumzentrierte Packung
3.1 Abgestumpftes Oktaeder oder abgestumpfter Wrfel
Die Abbildung 5 zeigt ein abgestumpftes Oktaeder. Es entsteht durch Abschleifen der sechs Spitzen des Oktaeders (magenta in Abb. 5), bis die gleichseitigen Dreiecke zu regelm§igen Sechsecken (zyan in Abb. 5) geworden sind.

Abb. 5: Abgestumpftes Oktaeder
Dieselbe Figur entsteht, indem zunchst ein Wrfel durch die Mittelnormalebene halbiert wird (Abb. 6) und dann acht solche halbe Wrfel Rcken an Rcken zusammengeklebt werden. Wir knnen also auch von einem abgestumpften Wrfel reden.

Abb. 6: Halber Wrfel
Diese aus sechs Quadraten und acht regelm§igen Sechsecken bestehenden halbregulren Figuren sind ebenfalls Raumfller (Abb. 7). Es ergibt sich eine kubisch raumzentrierte Packung. Wir bentigen vier Farben. Die Farben rot und grn bilden ein kubisches Gitter wie beim rumlichen Schachbrett, ebenso die Farben blau und gelb. Wir haben sozusagen zwei ineinandergemurkste rumliche Schachbretter.
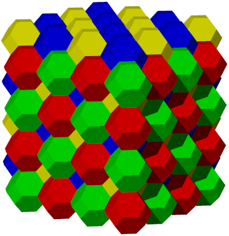
Abb. 7: Kubisch raumzentriert
Es geht
auch mit einer Pyramide (Abb. 8). Die Seitenflchen der Pyramide haben gegenber
der Grundflche immer noch einen Neigungswinkel 45¡. Das scheint auf den ersten
Blick nicht zu stimmen, denn wir zhlen sowohl auf der Bodenkante wie auf einer
Schrgkante acht abgestumpfte Oktaeder und knnten in Versuchung geraten, die
Seitendreiecke als gleichseitig anzusehen. Das ergbe gegenber den Grundebene
einen Neigungswinkel ![]() . Die Fehlberlegung liegt in Folgendem. In der
Grundkante sto§en die Einheiten in den Quadraten zusammen, in einer Schrgkante
in regelm§igen Sechsecken. Die Durchmesser der abgestumpften Oktaeder zwischen
zwei gegenberliegenden Quadraten und zwei gegenberliegenden Sechsecken verhalten
sich wie
. Die Fehlberlegung liegt in Folgendem. In der
Grundkante sto§en die Einheiten in den Quadraten zusammen, in einer Schrgkante
in regelm§igen Sechsecken. Die Durchmesser der abgestumpften Oktaeder zwischen
zwei gegenberliegenden Quadraten und zwei gegenberliegenden Sechsecken verhalten
sich wie ![]() . Das hei§t insbesondere, dass eine Kugel, welche die
acht Sechseckmitten berhrt, die sechs Quadratseiten nicht erreicht. Es gibt keine Inkugel, welche alle 14 Seiten
berhrt. Das hat zur Folge, dass es mit Kugeln einfacher geht.
. Das hei§t insbesondere, dass eine Kugel, welche die
acht Sechseckmitten berhrt, die sechs Quadratseiten nicht erreicht. Es gibt keine Inkugel, welche alle 14 Seiten
berhrt. Das hat zur Folge, dass es mit Kugeln einfacher geht.
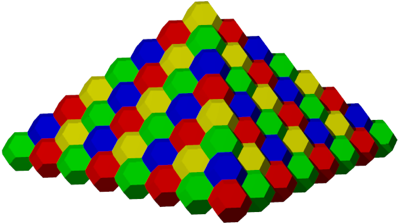
Abb. 8: Pyramide
3.2 Mit Kugeln
Bei der entsprechenden Anordnung mit Kugeln bentigen wir nur zwei Farben (Abb. 9). Wir knnen die Farben schichtenweise abwechseln. Aber wir haben jetzt natrlich keinen Raumfller.
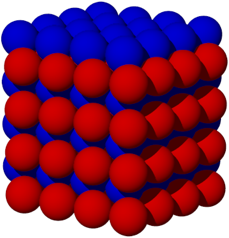
Abb. 9: Bei Kugeln gengen zwei Farben
Kugeln gleicher Farbe berhren sich nicht, wie eine Detailsicht von der Seite lehrt (Abb. 10).
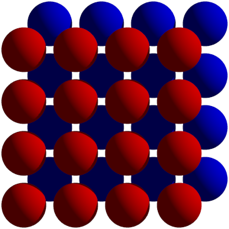
Abb. 10: Kugeln gleicher Farben berhren sich nicht
Das gilt natrlich auch fr die Pyramide (Abb. 11).
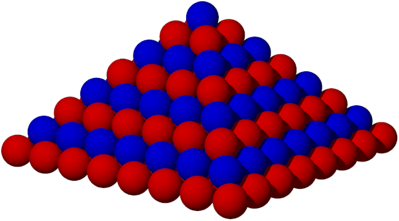
Abb. 11: Kugelpyramide mit zwei Farben
3.3 Mit Kreuzen
Wir arbeiten mit einem Kreuz der Abbildung 12. Das Kreuz besteht aus einem zentralen Wrfel, dem halb so hohe Quader aufgesetzt sind.

Abb.12: Es is halt a Kreiz. A Kreiz is!
Damit haben wir einen nicht konvexen Raumfller (Abb. 13). Wir bentigen vier Farben.

Abb. 13: Anordnung in einem gro§en Wrfel
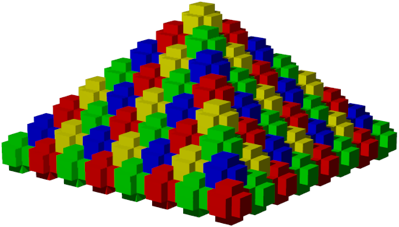
Abb. 14: Pyramide mit Kreuzen
3.4 Mit gelochten Wrfeln
Wir arbeiten mit einer Figur gem§ Abbildung 15. Es handelt sich hier um die Ergnzungsfigur des Kreuzes der Abbildung 12 zum Umwrfel, also zum kleinsten Wrfel, in welchem das Kreuz Platz findet.
Das Kreuz und seine Ergnzung haben dasselbe Volumen.
Die Figur ist mehrfach zusammenhngend und entspricht topologisch einer Tasse mit fnf Henkeln.

Abb. 15: Gelochter Wrfel
Trotzdem handelt es sich um einen Raumfller (Abb. 16). Er ist kubisch raumzentriert. Wir brauchen vier Farben. Die Teile sind ineinander verhngt. Am Rand der dargestellten Figur ist der Raum natrlich nicht vollstndig gefllt, aber im Innern schon.
Jedes Einzelteil ist mit acht Nachbarteilen verkettet.

Abb. 16: Raumfllung
Die Abbildung 17 zeigt die Pyramide. Ich gestehe, dass ich diese Studie nur geschrieben habe, um diese Figur vorstellen zu knnen.
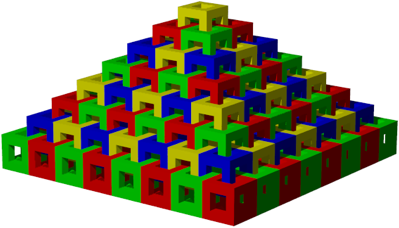
Abb. 17: Pyramide
3.5 Mit gelochten Wrfeln. Variante
Wir knnen analog mit der Ergnzung des abgestumpften Oktaeders (Abb. 5) zum umgebenden Wrfel arbeiten (Abb. 18).

Abb. 18: Ergnzung des abgestumpften Oktaeders zum Wrfel
Am besten stellt man sich acht Elemente der Abbildung 6 an den magenta Dreiecken zu einem Wrfel zusammengeklebt vor. Die Topologie ist dieselbe wie beim gelochten Wrfel der Abbildung 15.
Die Abbildung 19 zeigt die Packung. Sie ist immer noch kubisch raumzentriert. Wir brauchen vier Farben.
Am Rand haben wir wiederum Hohlrume, im Innern nicht.

Abb.19: Packung
Die Abbildung 20 zeigt die Pyramide.
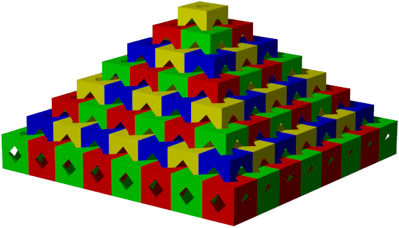
Abb. 20: Pyramide
Die bisherigen Raumfller haben alle die Symmetrien von Wrfel / Oktaeder. Das muss nicht so sein.
3.6 Raumfller mit Tetraeder-Symmetrie
Wir arbeiten mit dem Raumfller der Abbildung 21. Er hat nur noch die Symmetrien des Tetraeders,

Abb. 21: Raumfller
Die Abbildung 22 zeigt die bliche Packung. Sie ist kubisch raumzentriert.
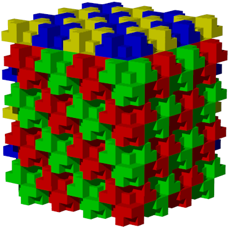
Abb. 22: Packung
Die Abbildung 23 zeigt zwei rote und zwei grne Fller-Elemente in derselben Etage. Wir sehen, dass sie sich alle diese Fller-Elemente nur lngs Kanten berhren. Wir drfen dafr also die gleiche Farbe verwenden.

Abb. 23: Vier benachbarte Fller-Elemente
Fr die Packung kommen wir daher mit nur zwei Farben durch (Abb. 24).

Abb. 24: Zwei Farben gengen
Die Abbildung 25 zeigt die entsprechende Pyramide.
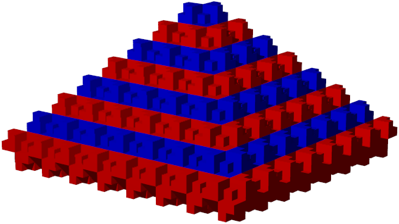
Abb. 25: Pyramide
4 Kubisch flchenzentrierte Packungen
4.1 Rhombendodekaeder
Wenn wir auf allen sechs Seiten eines Wrfels eine Pyramide mit Neigungswinkel 45¡ gegenber der Grundflche aufsetzten, entsteht ein Rhombendodekaeder (Abb. 26). Dies darum, weil die Seitenflchen benachbarter Pyramiden glatt ineinander bergehen. Wir erhalten damit zwlf Rhomben als Seitenflchen, daher der Name

Abb. 26: Rhombendodekaeder
Das Rhombendodekaeder ist ein Raumfller. Es ergibt sich eine kubisch flchenzentrierte Packung. Wir bentigen vier Farben.
Die Abbildung 27 zeigt die unterste Schicht mit den roten und den grnen Rhombendodekaedern.

Abb. 27: Unterste Schicht
Die Abbildung 28 zeigt die Situation von oben.

Abb. 28: Situation von oben
Die Abbildung 29 zeigt die unterste und die zweitunterste Schicht.

Abb. 29: Die beiden untersten Schichten
Die Abbildung 30 zeigt wiederum die Situation von oben.

Abb. 30: Situation von oben
Jetzt knnen wir eine Kopie der untersten Schicht drauflegen und so weiter.
Die Abbildung 31 zeigt die volle Packung.
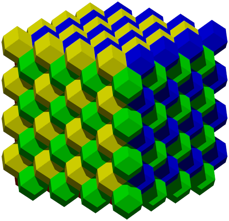
Abb. 31: Packung
4.2 Mit Kugeln
Mit den Inkugeln der Rhombendodekaeder knnen wir eine Kugelpackung bauen. Es handelt sich dabei um die dichtest mgliche Packung.
Die Abbildungen 32 und 33 zeigen die beiden untersten Schichten.
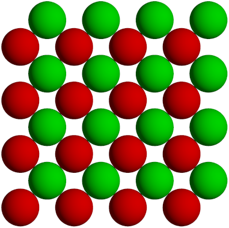
Abb. 32: Unterste Schicht
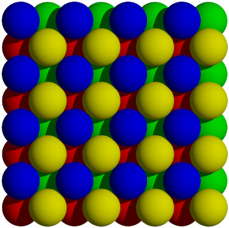
Abb. 33: Die unterste und die zweitunterste Schicht
Die Zentren der roten, grnen, blauen und gelben Kugel links oben in der Abbildung 33 bilden ein regulres Tetraeder.
Die Abbildung 34 zeigt die Packung.
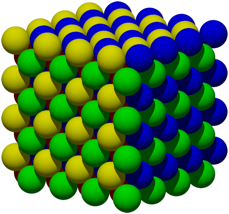
Abb. 34: Dichteste Kugelpackung
Wir whlen in der Abbildung 34 vorne-unten-mitte acht grne Kugeln aus (zwei davon sind im Inneren) welche die Ecken eines Wrfels bilden (Abb. 35).
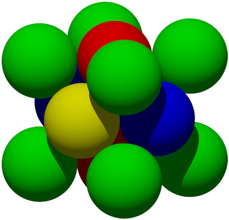
Abb. 35: Minimalauswahl
In den Seitenflchenmitten des Bodens und des Deckels dieses Wrfels sitzt je eine rote Kugel. In den Stein links und rechts sitzt je eine blaue Kugel, und in der Frontflche und der Hinterflche je eine gelbe Kugel. Dies illustriert die Bezeichnung kubisch flchenzentriert.