Hans Walser, [20180714]

Minimalellipse

1     Problemstellung

Zu zwei kongruenten sich berŸhrenden Kreisen ist die flŠchenmŠ§ig kleinste Ellipse zu bestimmen, welche die beiden Kreise umfasst (Abb. 1).

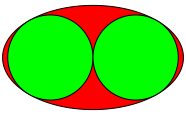
Abb. 1: Problemstellung

2     Bearbeitung

2.1    Konstruktion im allgemeinen Fall

Aus SymmetriegrŸnden hat die gesuchte Ellipse dieselben Achsen wie die Konfiguration aus den beiden gegebenen Kreisen.

Wir wŠhlen auf einem der beiden Kreise mit dem Mittelpunkt M1 einen laufenden Punkt P (Abb. 2a) und konstruieren die Ellipse, welche den Kreis in P berŸhrt.

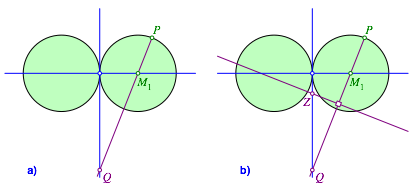
Abb. 2: Erste Schritte der Konstruktion

Dazu schneiden wir die Gerade PM1 mit der senkrechten Achse und erhalten so den Punkt Q.

Die Mittelsenkrechte der Strecke PQ schneiden wir ebenfalls mit der senkrechten Achse und erhalten den Punkt Z.

Den Kreis z um Z durch P (und Q) schneiden wir mit der waagerechten Achse in den beiden Punkten F1 und F2 (Abb. 3a).

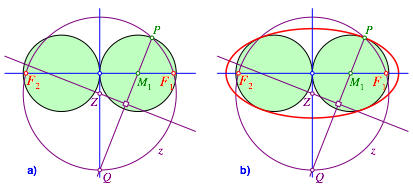
Abb. 3: Brennpunkte und Ellipse

Diese beiden Punkte sind die Brennpunkte der gesuchten Ellipse. Zusammen mit P haben wir die nštigen Informationen fŸr die Ellipse.

Die Stimmigkeit dieser Konstruktion ergibt sich aus [1].  

2.2    Berechnungen fŸr den optimalen Fall

Wir verwenden die Symmetrieachsen als Achsen des kartesischen Koordinatensystems. Die Einheit sei der Radius der beiden gegebenen Kreise. Den Punkt P parametrisieren wir mit:

 

                                                                                     (1)

 

 

Damit rechnen wir die Konstruktion gemŠ§ den Abbildungen 2 und 3 durch und erhalten den FlŠcheninhalt der Ellipse als Funktion von t. Schlie§lich muss noch die Ableitung dieser Funktion null gesetzt werden. Mit CAS erhalten wir im relevanten Bereich die Lšsung:

 

                                                                                                                                (2)

 

 

Die Abbildung 4 zeigt rot den Funktionsgrafen der FlŠchenfunktion und blau die Ableitung. Das Minimum ist bei .

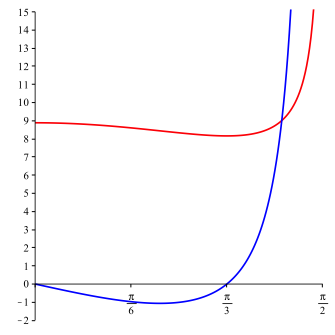
Abb. 4: FlŠchenfunktion und Ableitung

Die Abbildung 1 zeigt den optimalen Fall.

3     Diskussion des optimalen Falles

Im optimalen Fall, also fŸr  erhalten wir die Ellipsenachsen:

 

                                                                                (3)

 

 

Der FlŠcheninhalt der Ellipse ist:

 

                                                                                     (4)

 

 

Die Abbildung 5 zeigt nochmals die Minimallšsung. Der Punkt Z (vgl. Abb. 3) ist nun im Zentrum der Figur. Die Figur lŠsst sich weitgehend in ein regulŠres Dreiecksraster einpassen.

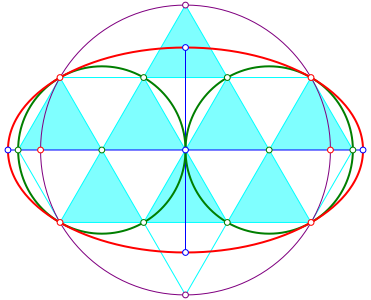
Abb. 5: Minimallšsung

In der Abbildung 6 ist zusŠtzlich ein schrŠges gelbes Rechteck eingezeichnet. Es hat genau den FlŠcheninhalt 3. Zudem finden wir Winkel von 45¡.

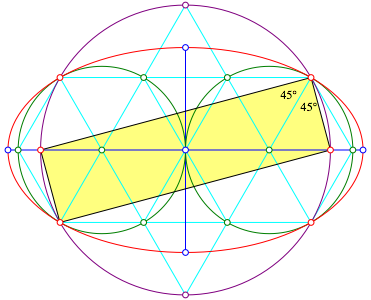
Abb. 6: SchrŠges Rechteck

4     Allgemeiner Fall

Die beiden gegebenen Kreise brauchen sich nicht zu berŸhren (Abb. 7). Die Minimallšsung liefert dann allerdings keine ãschšnenÒ Resultate.

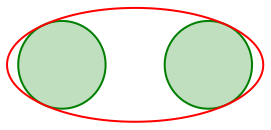
Abb. 7: Allgemeiner Fall

Weblinks

[1] Hans Walser, Dreiecksaufgabe (15.07.2018):

www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksaufgabe/Dreiecksaufgabe.htm