Hans Walser, [20230745]
Mittelpunkt
Anregung: Thomas Jahre, Chemnitz
1 Worum es geht
Problem der Mitte im geografischen Kontext
Schöne Figuren im geometrischen Kontext. Reuleaux-Dreieck. Bahnkurven
2 Einpacken ins Rechteck
Es gibt viele Verfahren, den Mittelpunkt eines Gebietes zu bestimmen.
Ein gelegentlich diskutiertes Verfahren geht wie folgt. Das Gebiet wird parallel zu einer Bezugsrichtung (oft wird dazu die Nordrichtung gewählt) in ein Rechteck eingepackt (Abb. 1).
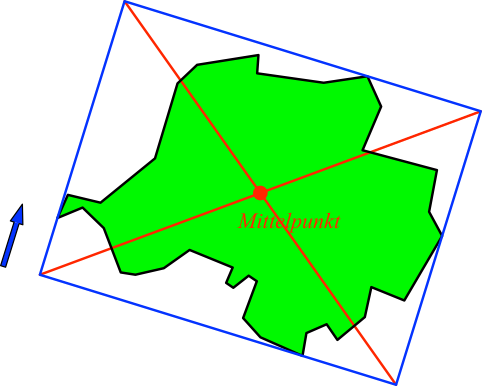
Abb. 1: Einpacken ins Rechteck
Der Mittelpunkt dieses Rechtecks, zum Beispiel durch die Diagonalen bestimmt, gilt dann als „Mittelpunkt“ des Gebietes.
3 Kritik
Das Verfahren ist abhängig von der gewählten Bezugsrichtung. Bei Änderung der Bezugsrichtung ändert auch der so konstruierte Punkt. Er ist also nicht intrinsisch mit dem Gebiet verbunden.
Die Abbildung 2 zeigt, wie der gemäß Abbildung 1 konstruierte Punkt sich bei Änderung der Bezugsrichtung bewegt.
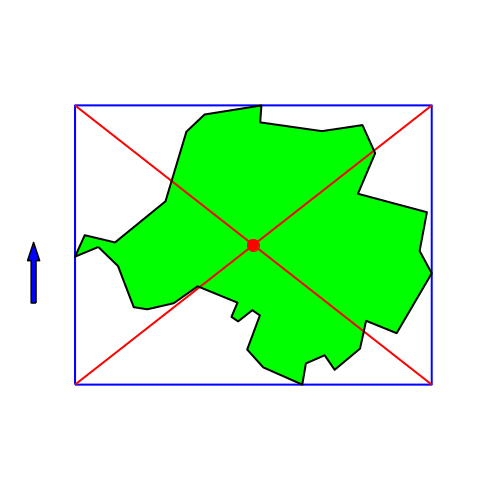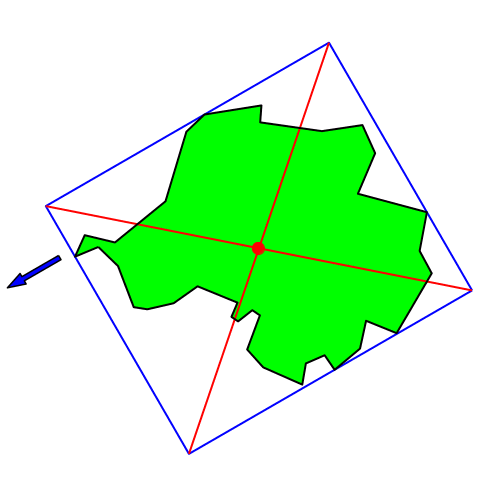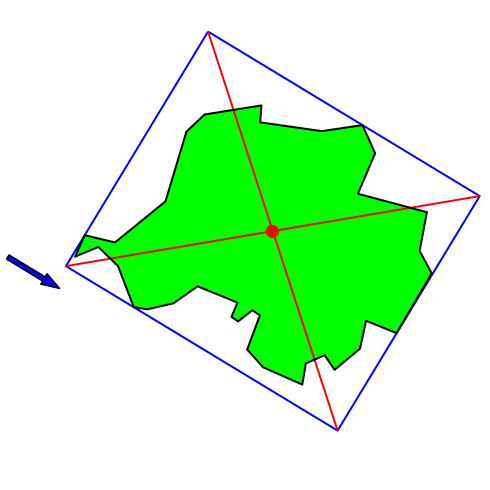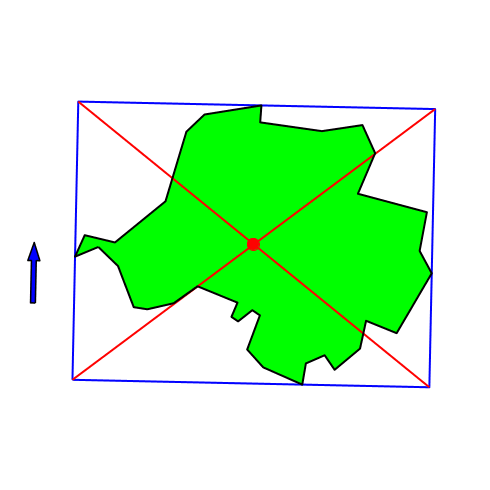
Abb. 2: Änderung der Bezugsrichtung
Die Abbildung 3 gibt die Bahnkurve des roten Punktes (vergrößert).

Abb. 3: Bahnkurve des roten Punktes (vergrößert)
4 Beispiele aus der Schulgeometrie
4.1 Punktsymmetrisches Gebiet
Bei einem punktsymmetrischen Gebiet ist das Verfahren konsistent. Es liefert bei jeder Bezugsrichtung das Symmetriezentrum des Gebietes.
4.2 Gleichseitiges Dreieck
Bei einem gleichseitigen Dreieck (Abb. 4 und 5) liefert das Verfahren in keinem Fall den Mittelpunkt des Dreiecks.
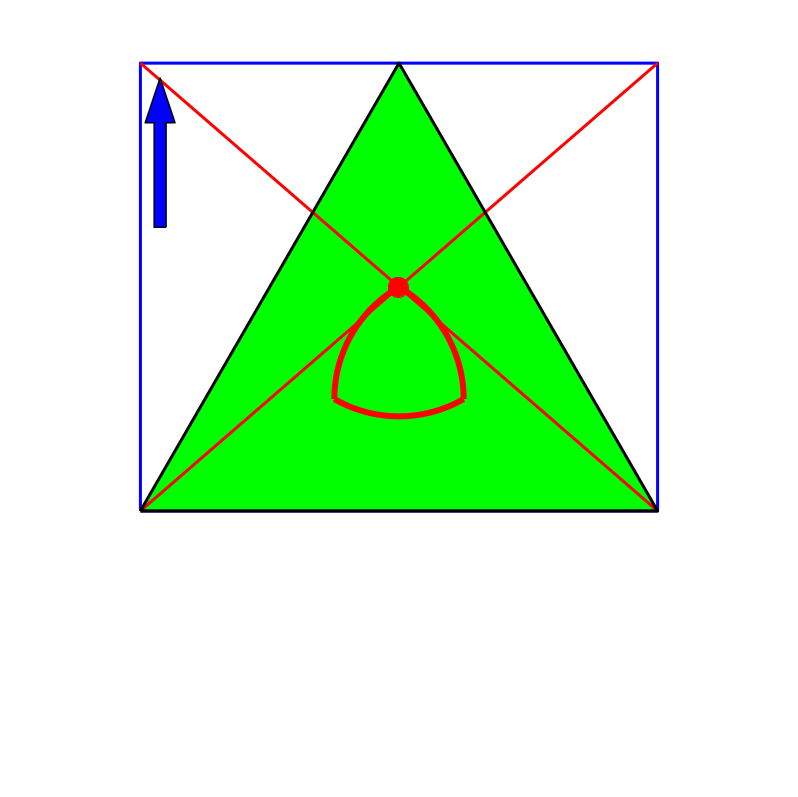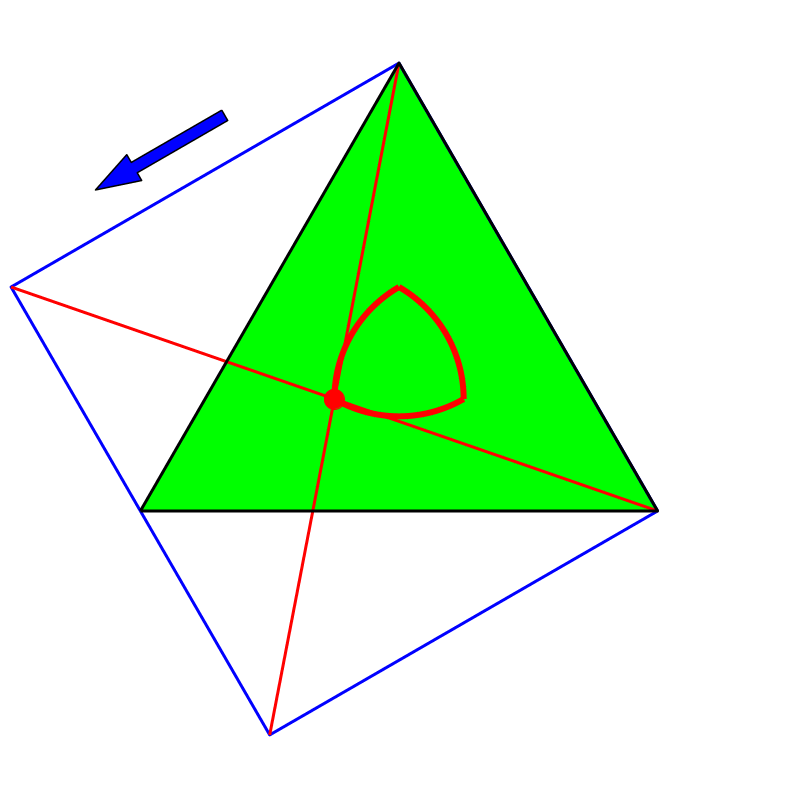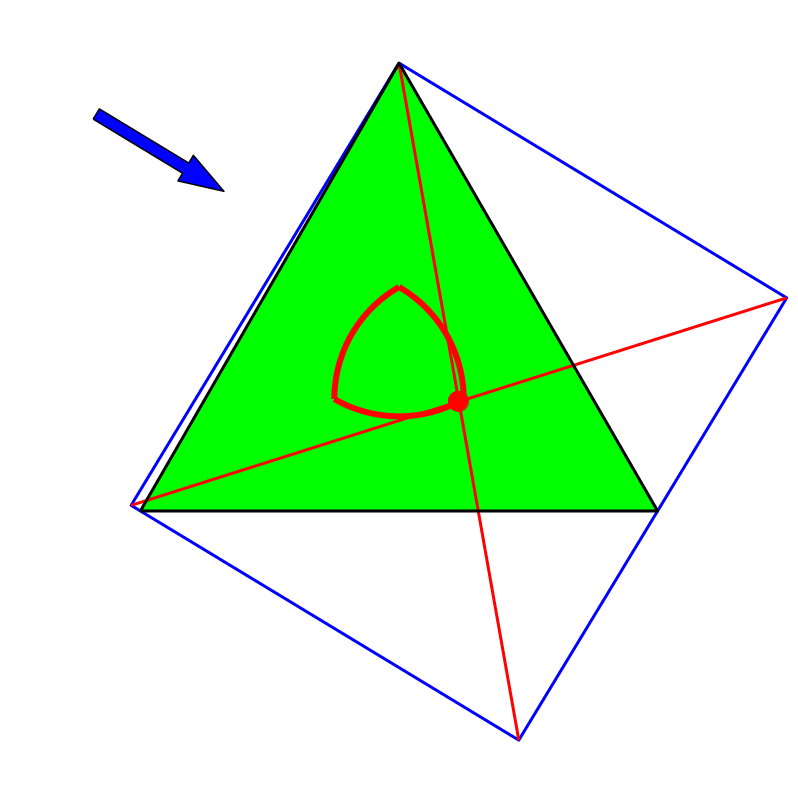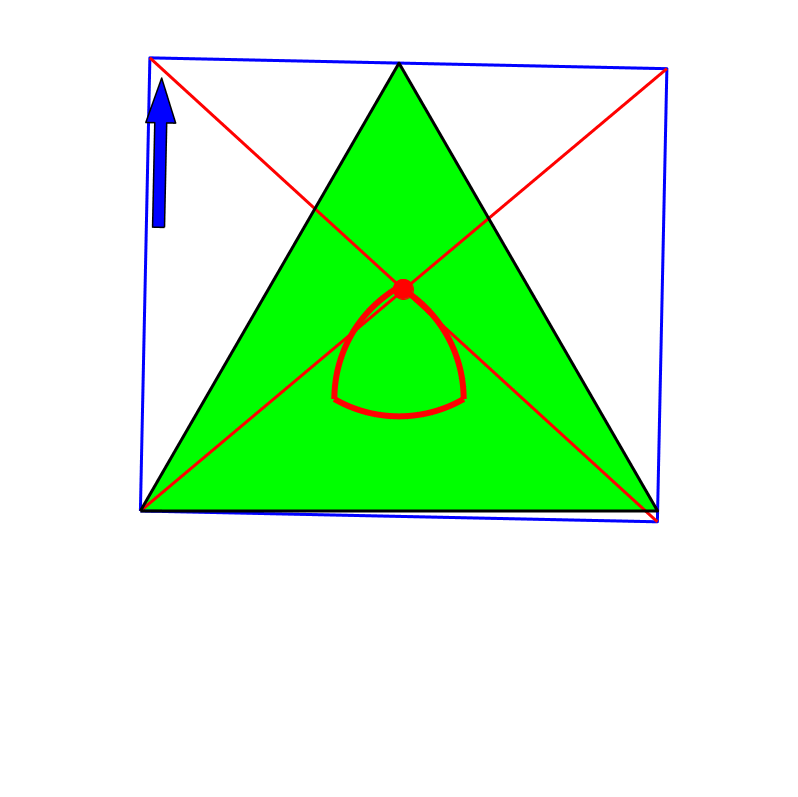
Abb. 4: Gleichseitiges Dreieck
Die nach dem Verfahren konstruierten Punkte variieren in Abhängigkeit der Bezugsrichtung auf einem Reuleaux-Dreieck.
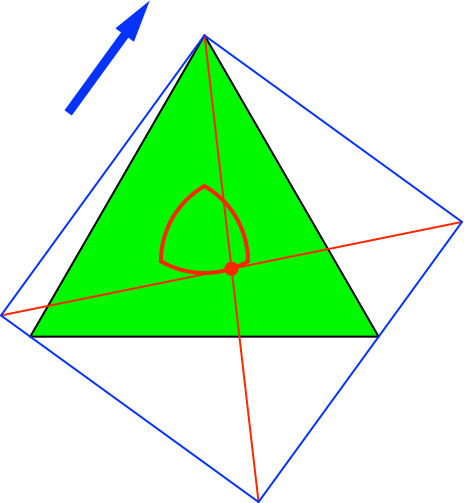
Abb. 5: Reuleaux-Dreieck
Die Abbildung 6 zeigt die Konstruktion dieses Reuleaux-Dreieckes. Die Mittelpunkte der Reuleaux-Kreise sind die Mittelpunkte der Dreieckshöhen.
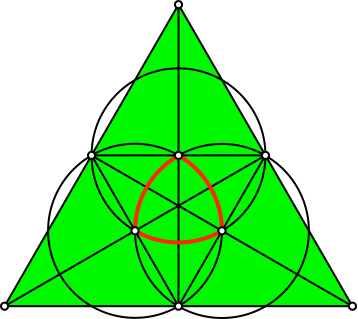
Abb. 6: Konstruktion des Reuleaux-Dreieckes
4.3 Quadrat
Da das Quadrat punktsymmetrisch ist, liefert das Verfahren immer den Mittelpunkt (Abb. 7).

Abb. 7: Quadrat
Das umbeschriebene Rechteck ist immer ein Quadrat, ändert aber seine Größe.
4.4 Regelmäßiges Fünfeck
Auch bei einem regelmäßigen Fünfeck (Abb. 8 und 9) liefert das Verfahren in keinem Fall den Mittelpunkt des Fünfeckes.
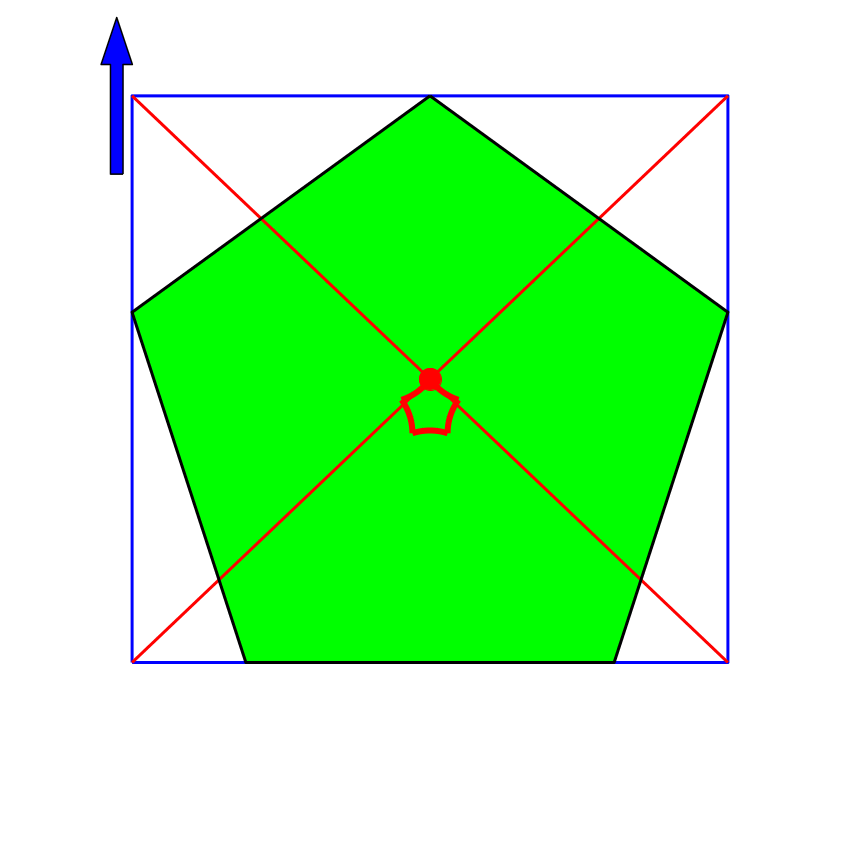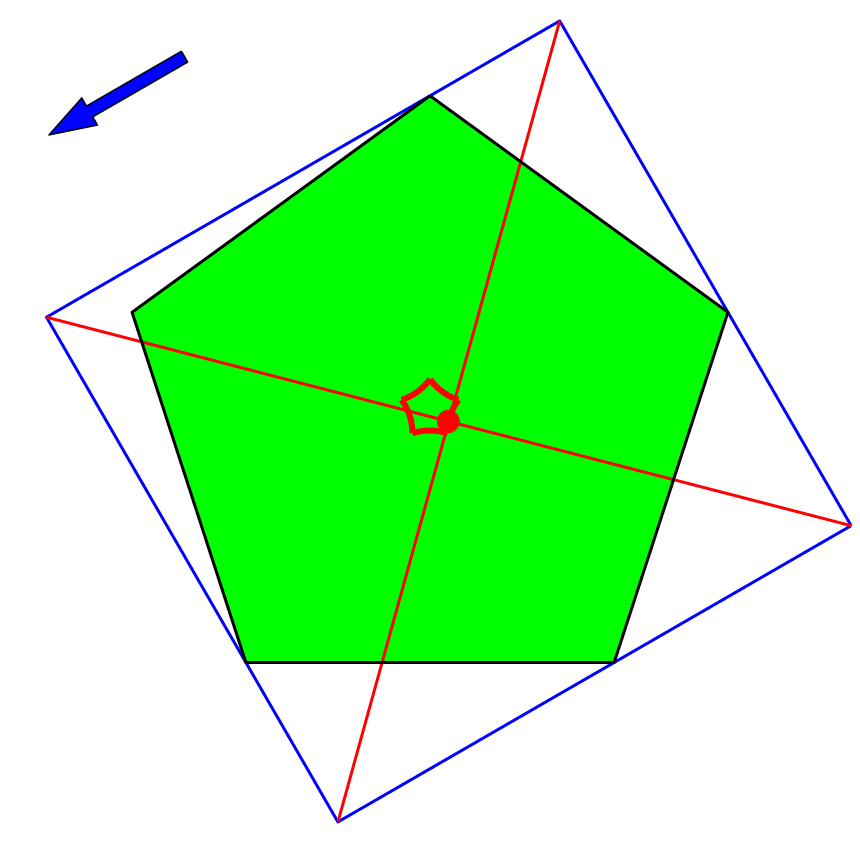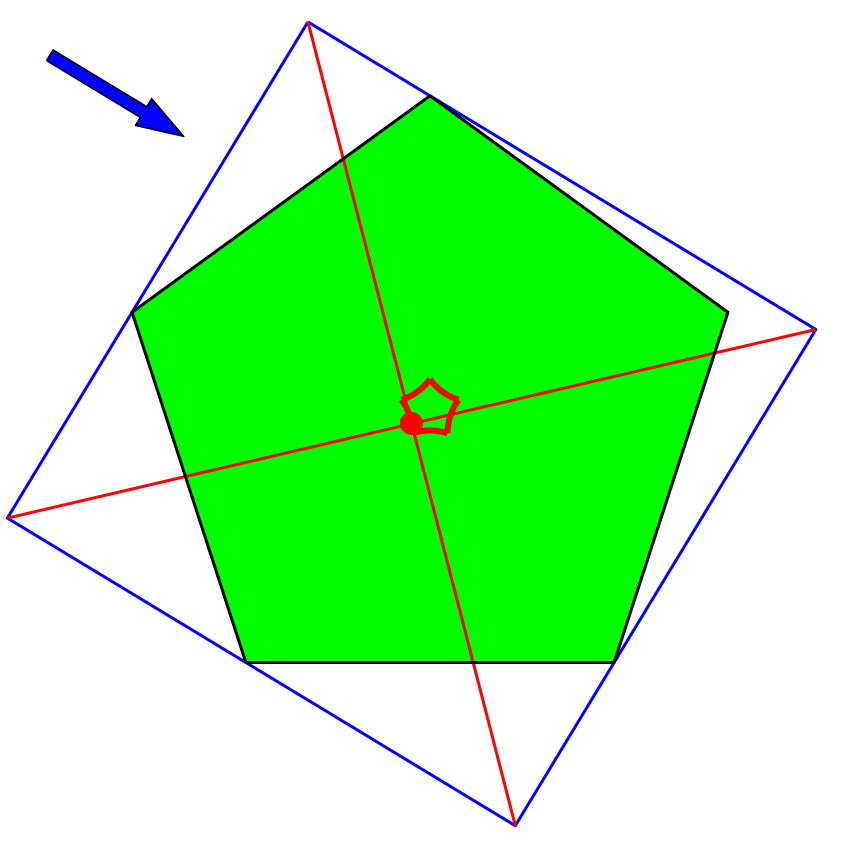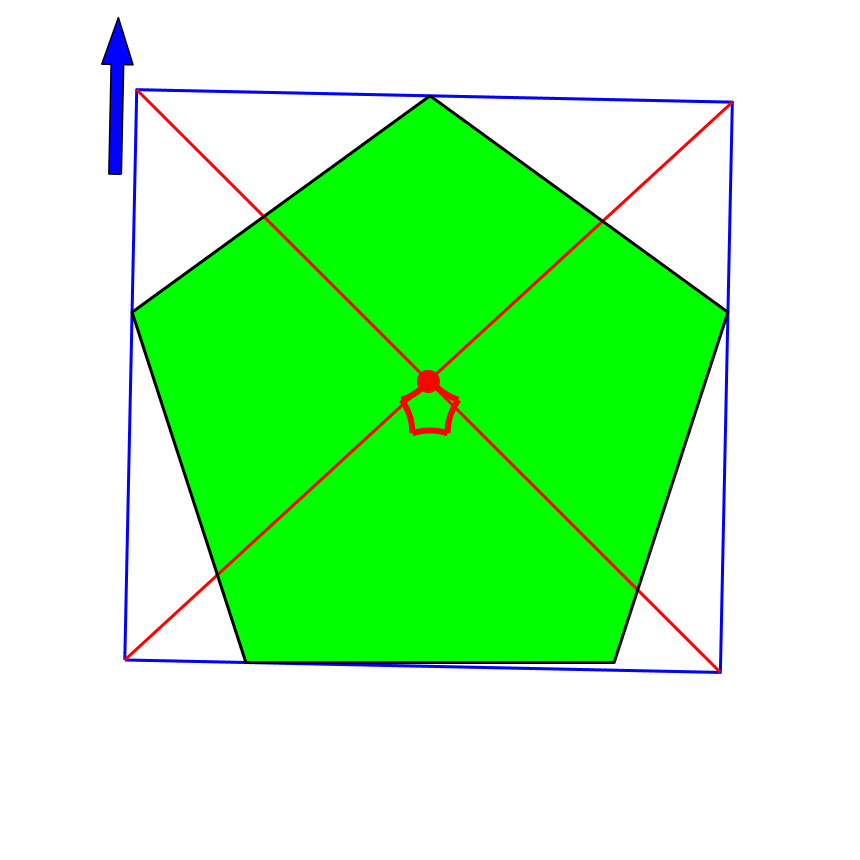
Abb. 8: Regelmäßiges Fünfeck
Die nach dem Verfahren konstruierten Punkte variieren auf einem Kreisbogenfünfeck, dessen Seiten nach innen gebogen sind.
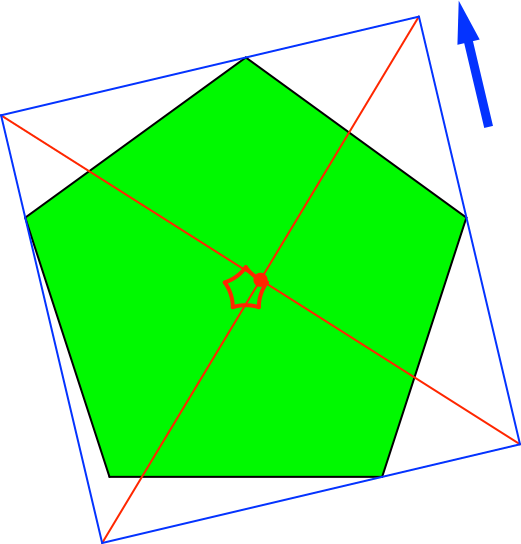
Abb. 9: Kreisbogenfünfeck
Die Abbildung 10 zeigt die Konstruktion dieses Kreisbogenfünfeckes.
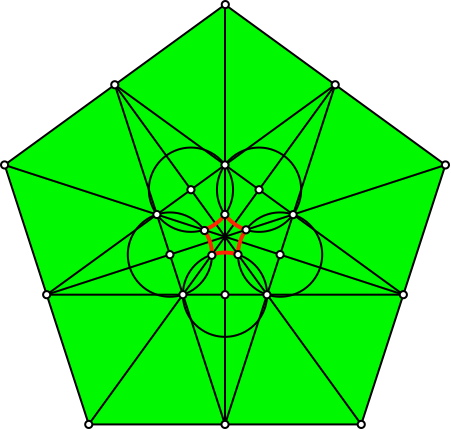
Abb. 10: Konstruktion des Kreisbogenfünfeckes
Die Figur enthält kollineare Punkte (Abb. 11, 12 und 13).
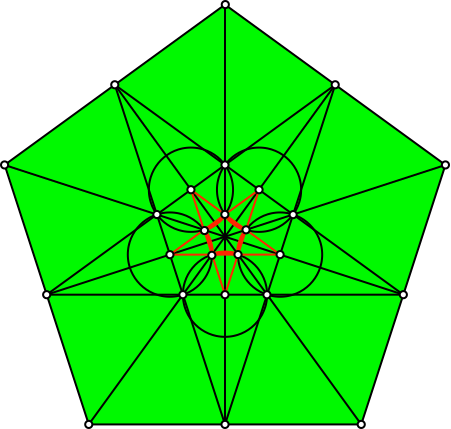
Abb. 11: Kollineare Punkte
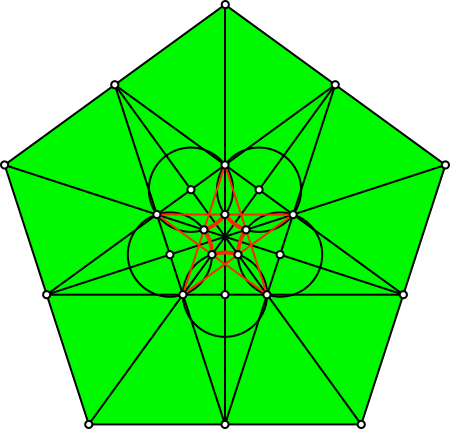
Abb. 12: Kollineare Punkte
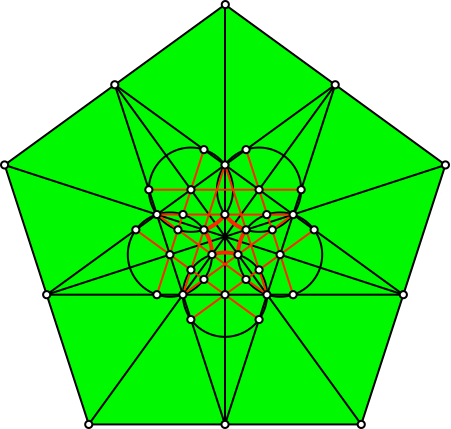
Abb. 13: Kollineare Punkte
4.5 Regelmäßiges Sechseck
Da das regelmäßige Sechseck punktsymmetrisch ist, gibt unser Verfahren immer den Mittelpunkt (Abb. 14).
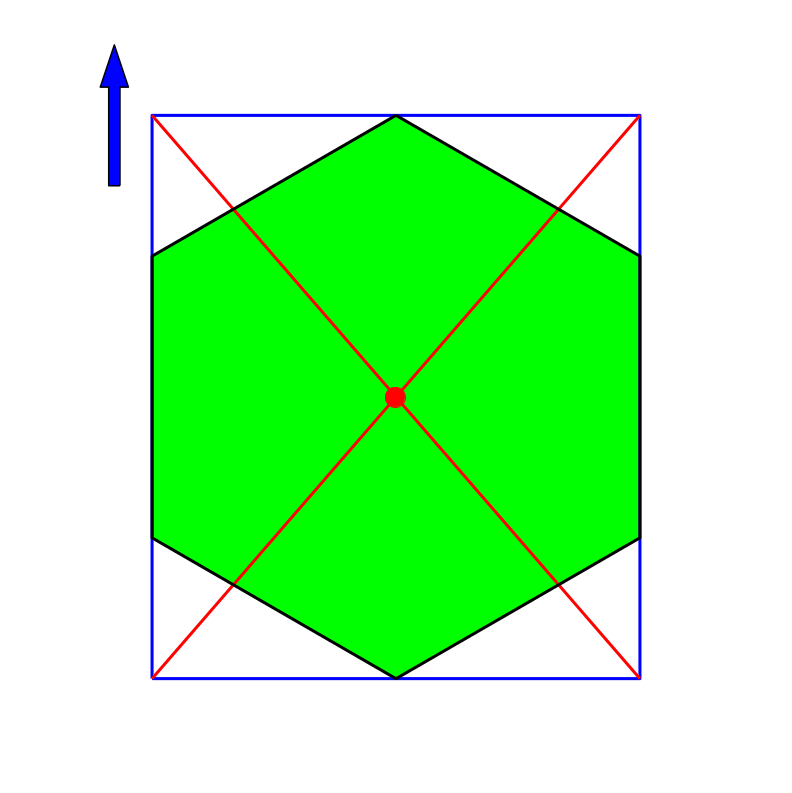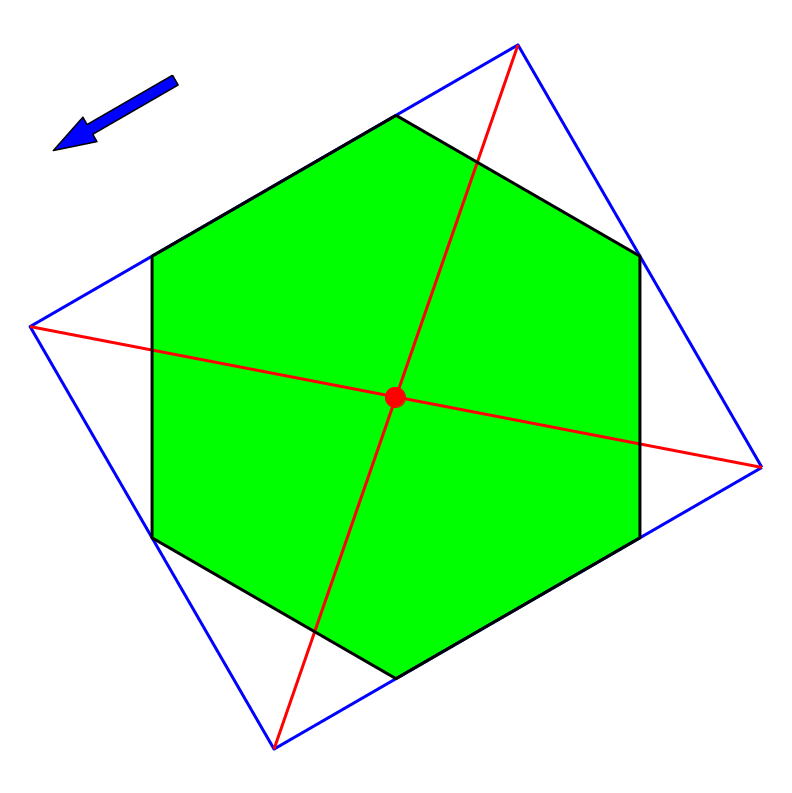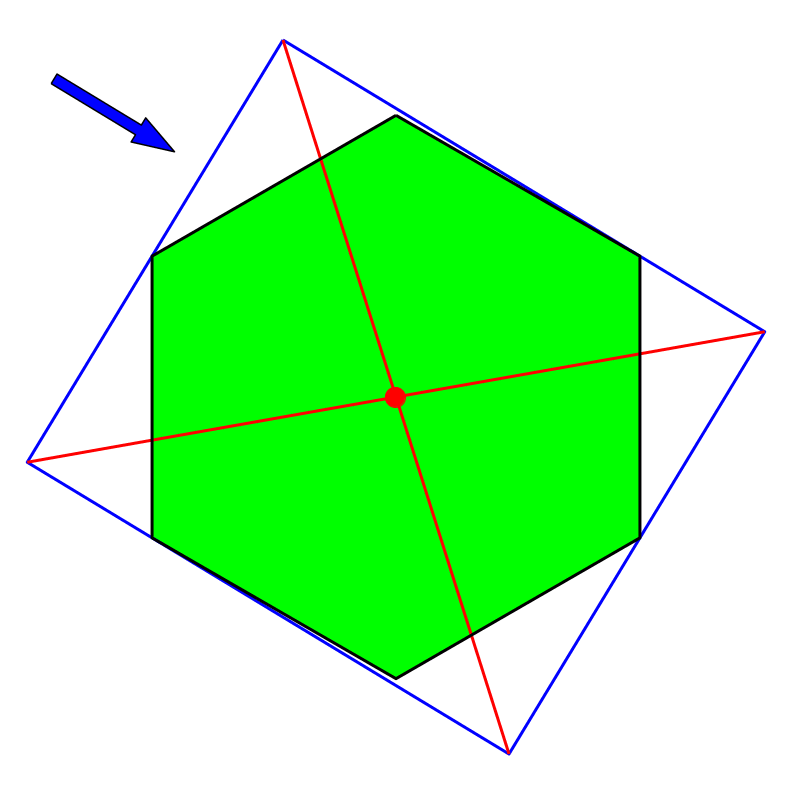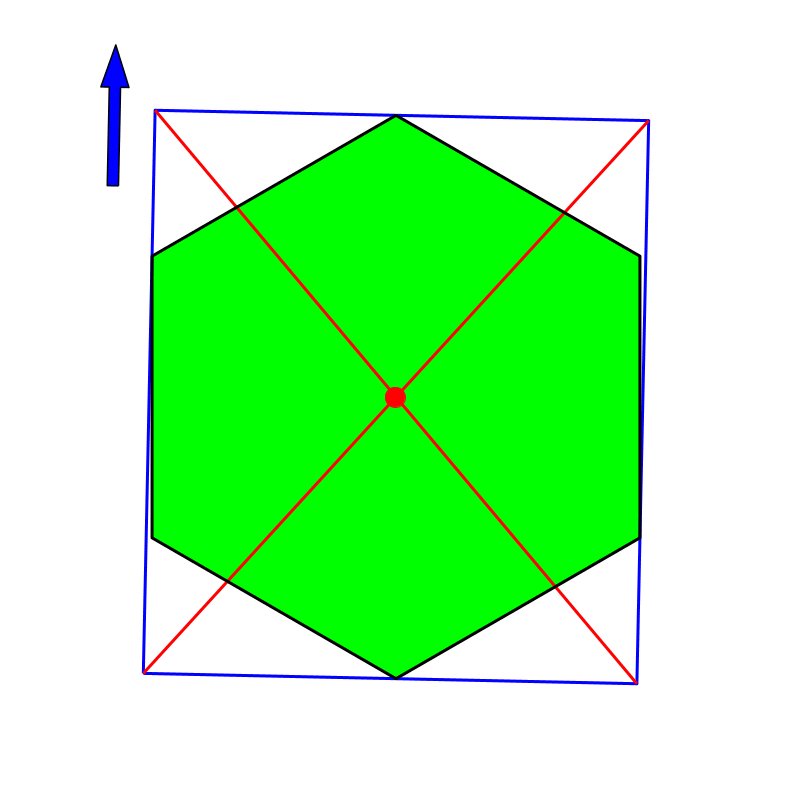
Abb. 14: Sechseck
4.6 Regelmäßiges Siebeneck
Im regelmäßigen Siebeneck ist der rote Punkt nicht stabil (Abb. 15).
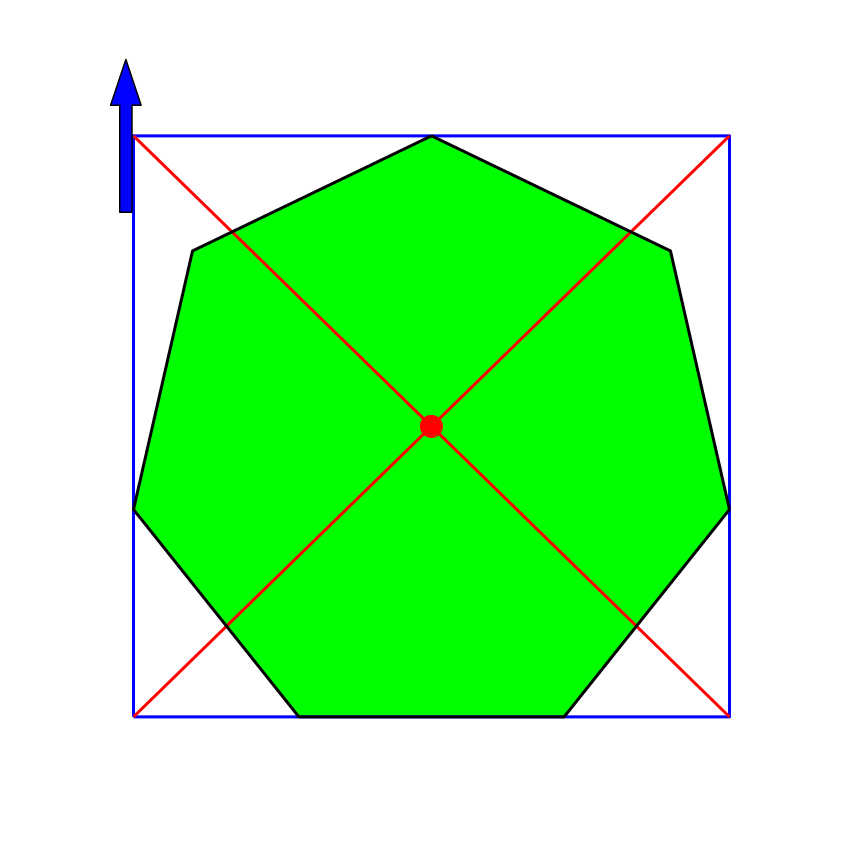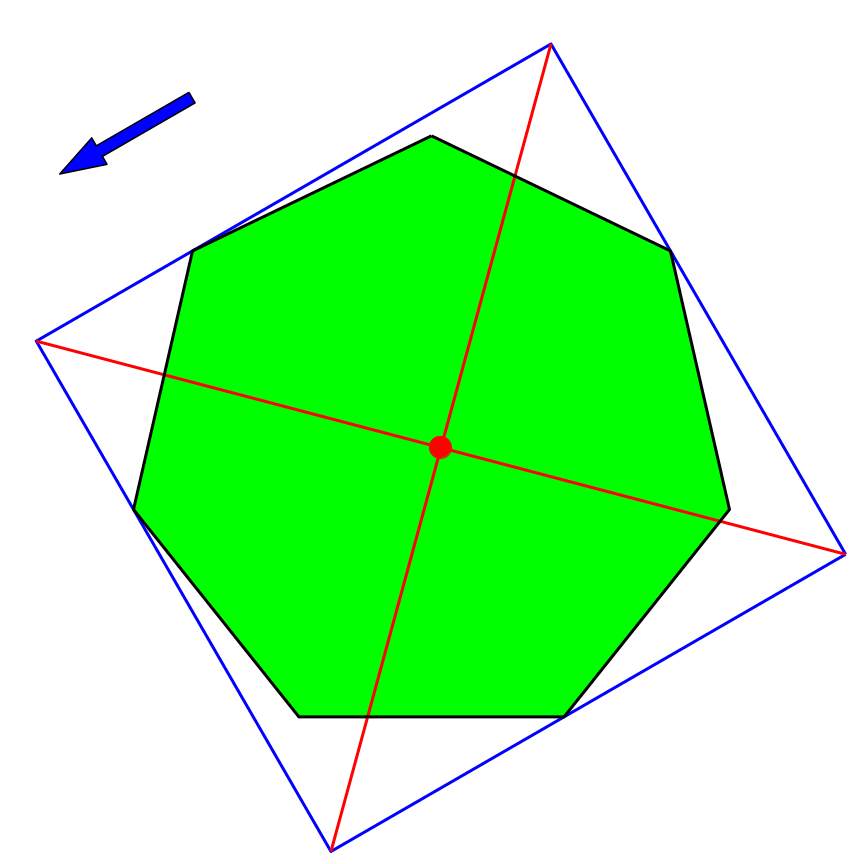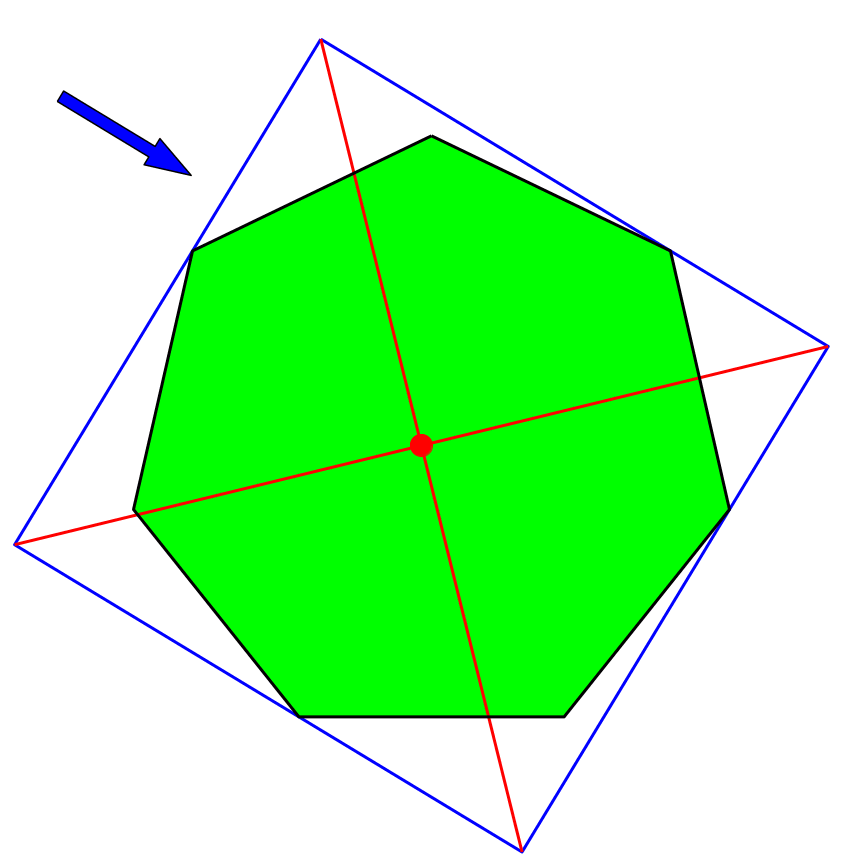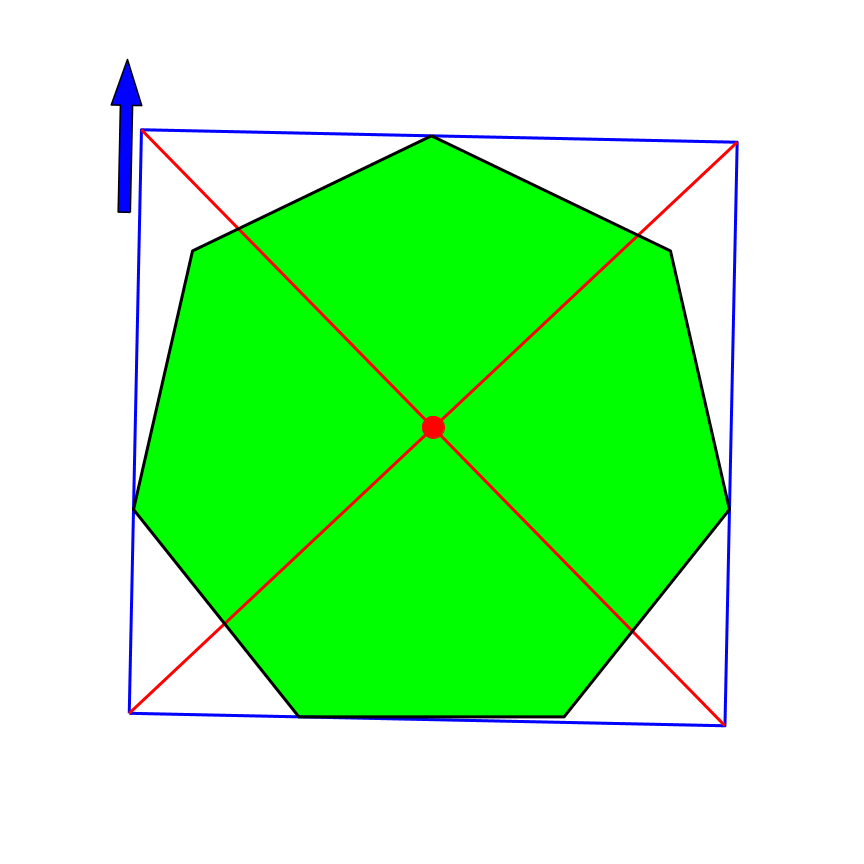
Abb. 15: Siebeneck
Die Abbildung 16 zeigt die Bahnkurve des roten Punktes. Die Bahnkurve ist ein Siebeneck mit nach außen gebogenen Kreisbogen. Es hat doppelten Umlauf.
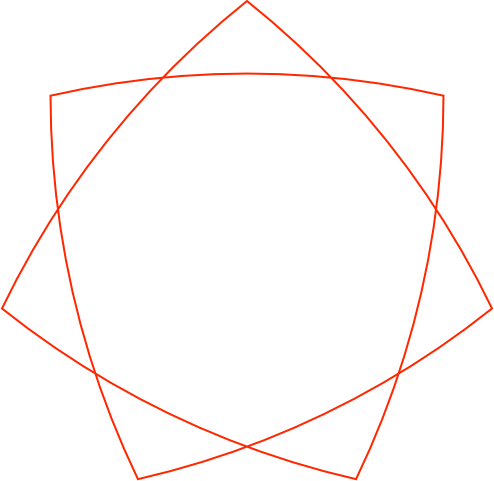
Abb. 16: Bahnkurve
4.7 Siebenzehneck
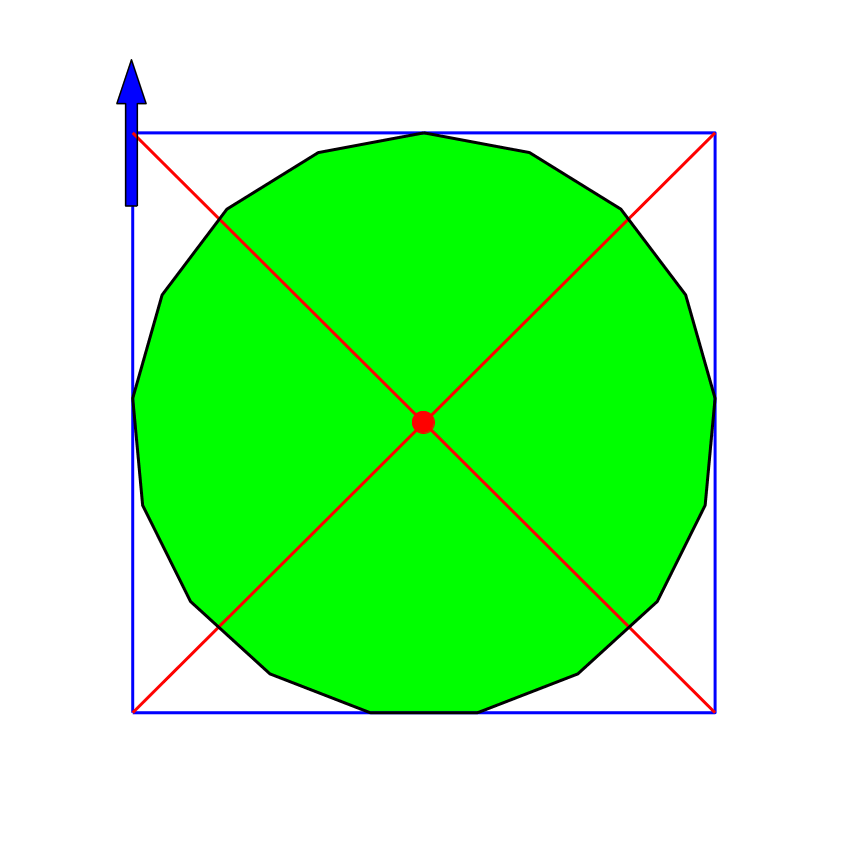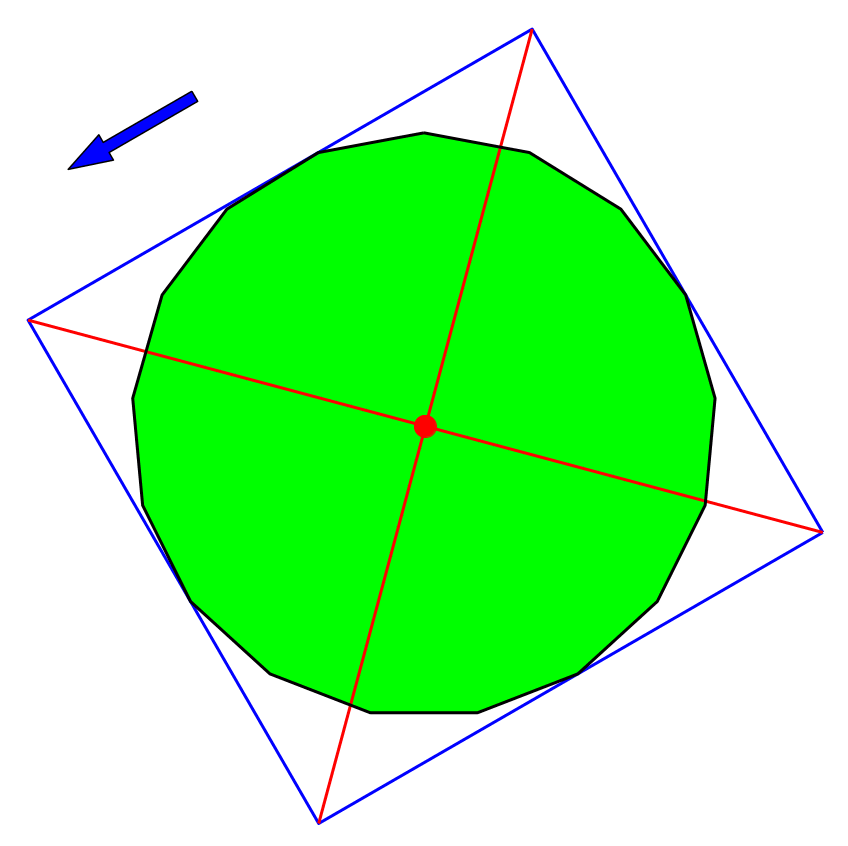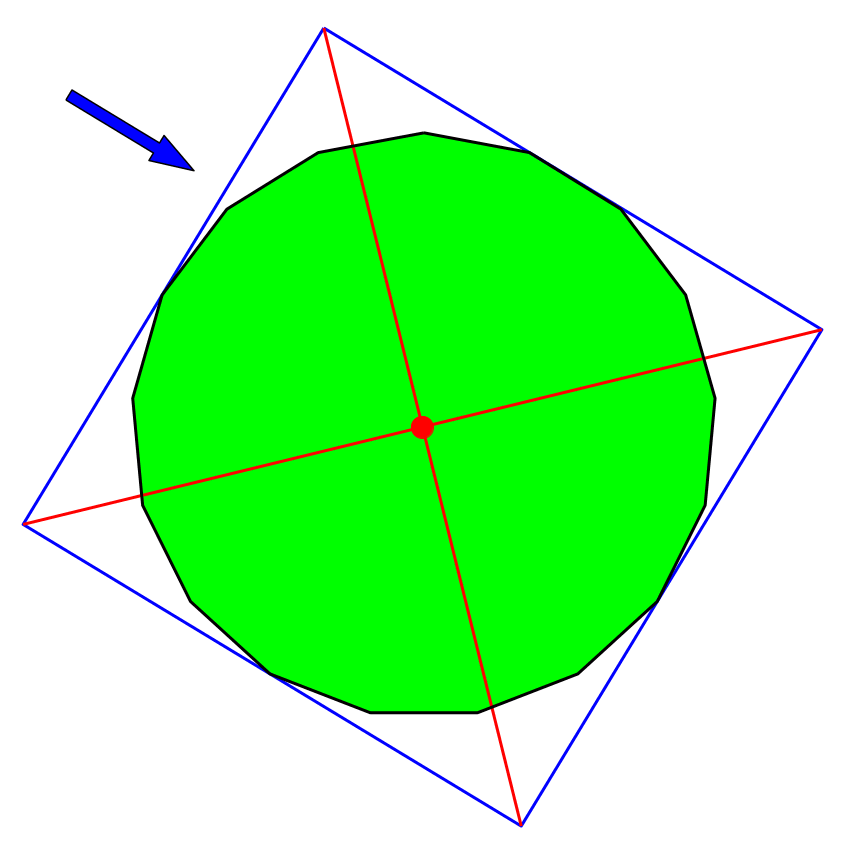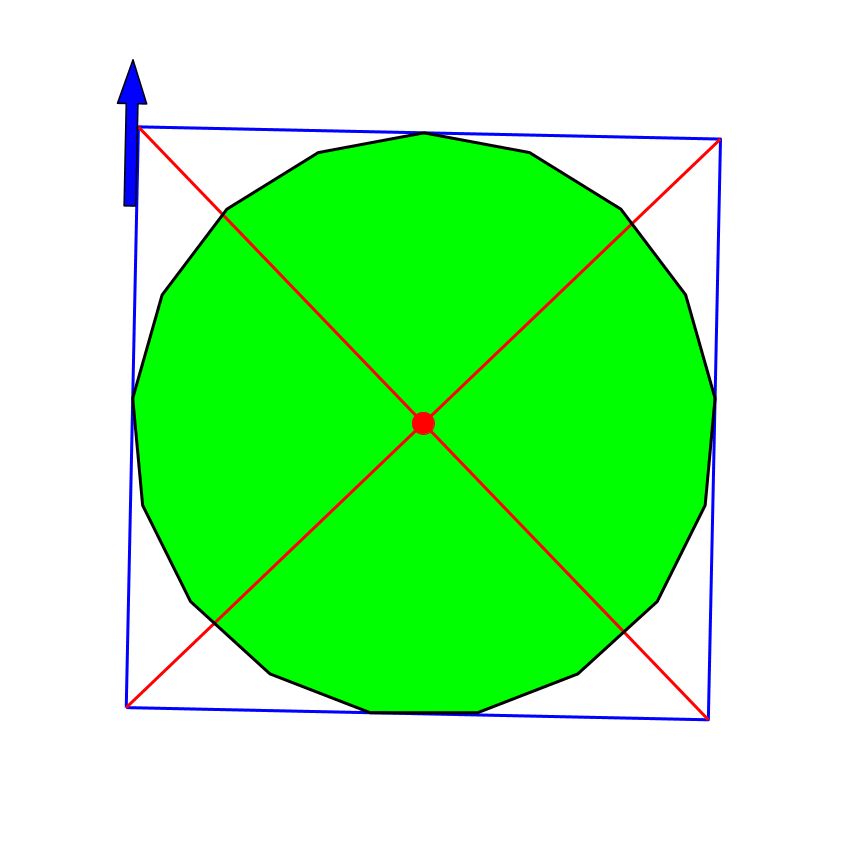
Abb. 17: Siebenzehneck

Abb. 18: Bahnkurve des roten Punktes
4.8 Bahnkurven
Die Abbildung 19 zeigt die Bahnkurven des roten Punktes bei regelmäßigen Vielecken mit 3, 5, 7, ... , 17 Ecken. Die Teilbilder sind auf einheitliche Ansichtsgröße skaliert.
Die Bahnkurven sind alternierend nach außen und innen gebogen. Bei jedem zweiten Schritt wächst die Umlaufzahl um eins.
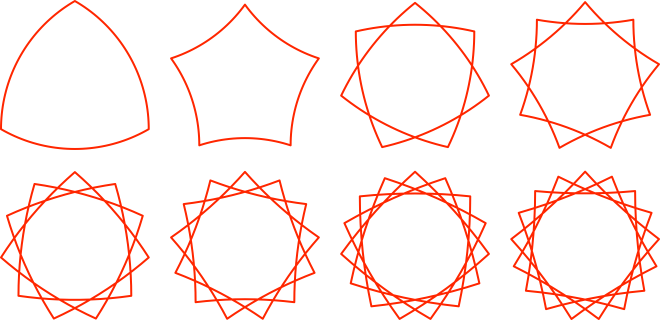
Abb. 19: Bahnkurven
Weblink
Thomas Jahre: Das Zentrum ist nicht die Mitte
https://www.schulmodell.eu/2704-das-zentrum-ist-nicht-die-mitte.html