Hans Walser, [20230746]

Mittelpunkt

1 Worum es geht

Problem der Mitte im geografischen Kontext

Schöne Figuren im schulgeometrischen Kontext. Bahnkurven

2 Einpacken ins Dreieck

Es gibt viele Verfahren, den Mittelpunkt eines Gebietes zu bestimmen.

Ein selten diskutiertes Verfahren geht wie folgt. Das Gebiet wird senkrecht zu einer Bezugsrichtung (häufig der Nordrichtung) in ein gleichseitiges Dreieck eingepackt (Abb. 1).

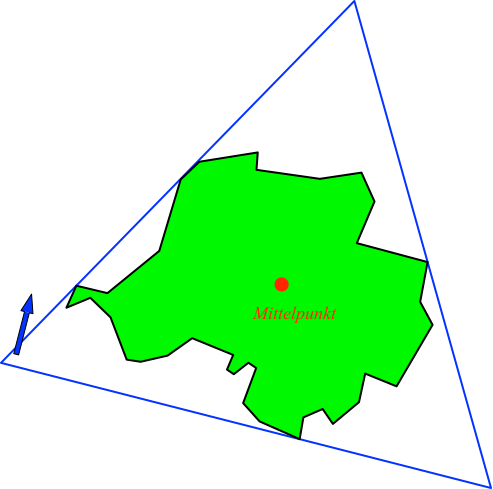
Abb. 1: Einpacken ins Dreieck

Der Mittelpunkt dieses Dreiecks gilt dann als „Mittelpunkt“ des Gebietes.

3 Kritik

Das Verfahren ist abhängig von der gewählten Bezugsrichtung. Bei Änderung der Bezugsrichtung ändert auch der so konstruierte Punkt. Er ist also nicht intrinsisch mit dem Gebiet verbunden.

Die Abbildung 2 zeigt, wie der gemäß Abbildung 1 konstruierte Punkt sich bei Änderung der Bezugsrichtung bewegt.

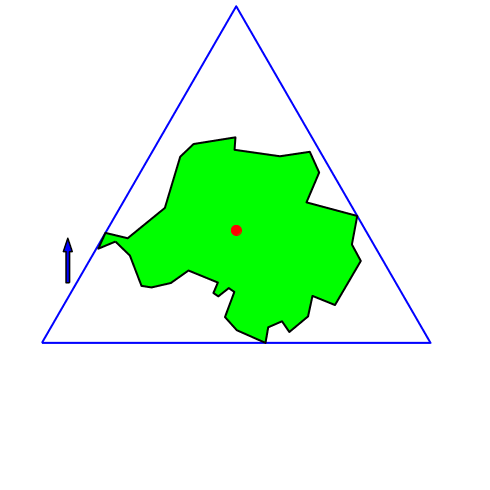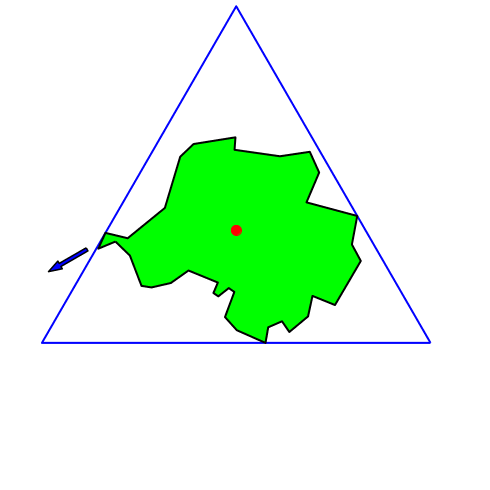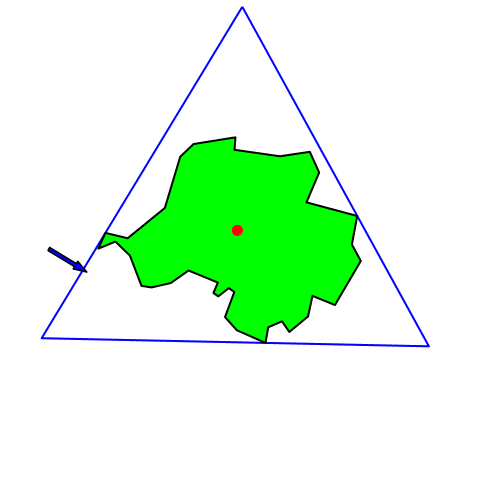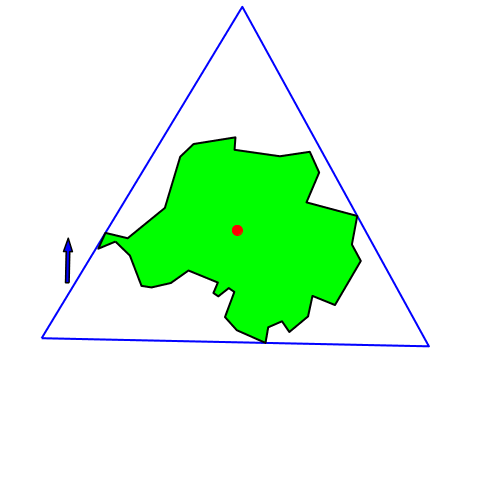
Abb. 2: Änderung der Bezugsrichtung

Die Abbildung 3 gibt die Bahnkurve des roten Punktes (vergrößert).

Abb. 3: Bahnkurve des roten Punktes (vergrößert)

4 Beispiele aus der Schulgeometrie

4.1 Strecke

„Eine Strecke hat einen und genau einen Mittelpunkt“. (unbekanntes Zitat)

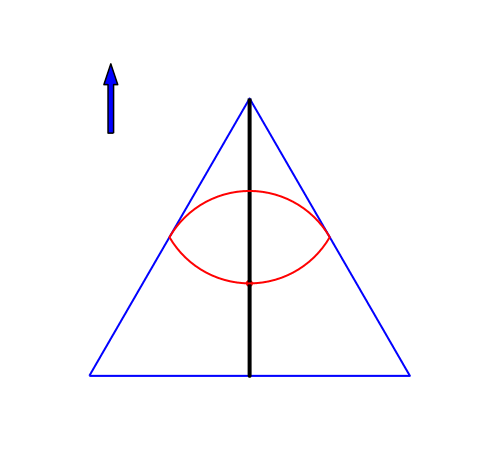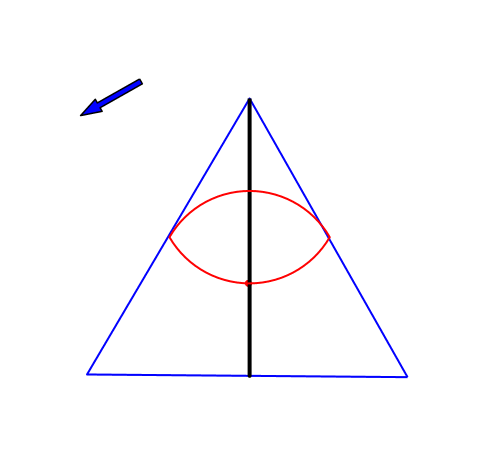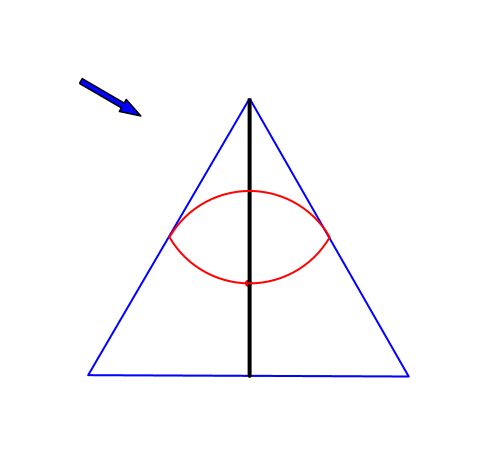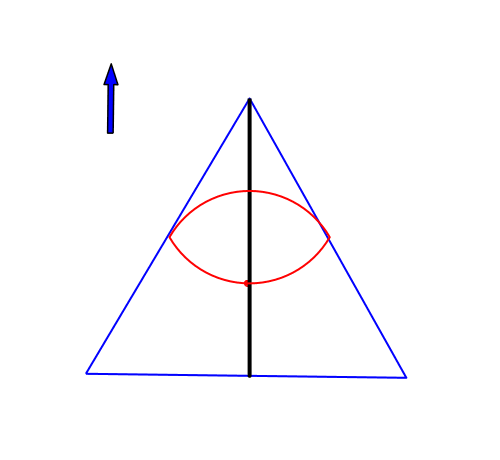
Abb. 4: Strecke

4.2 Gleichseitiges Dreieck

Beim gleichseitigen Dreieck bleibt der rote Punkt stabil und ist der Mittelpunkt des Dreieckes.

Abb. 5: Gleichseitiges Dreieck

4.3 Quadrat

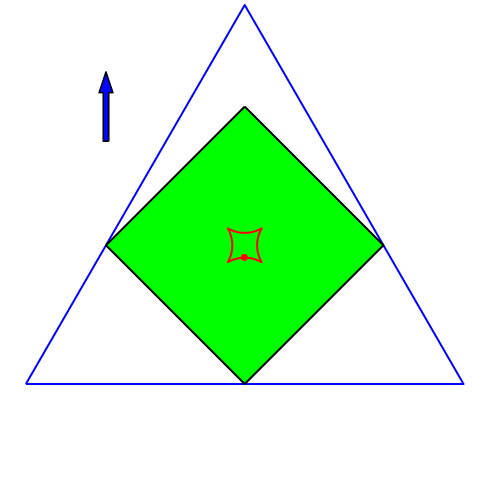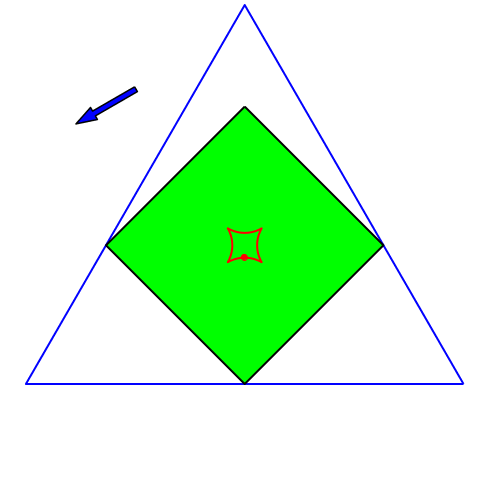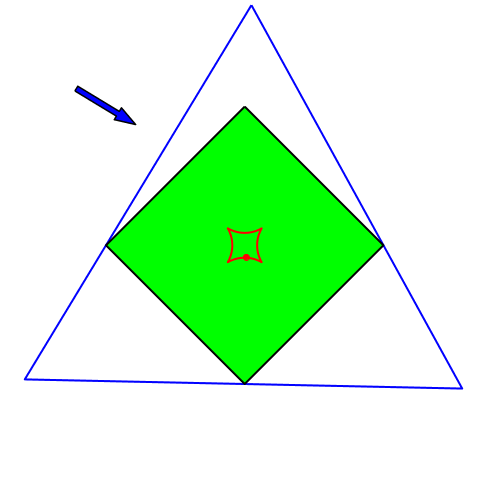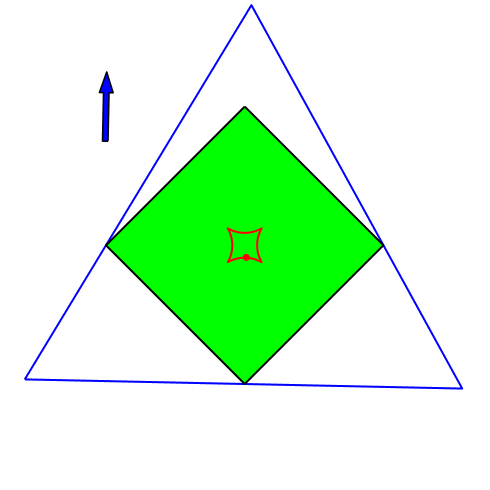
Abb. 6: Quadrat

4.4 Regelmäßiges Fünfeck

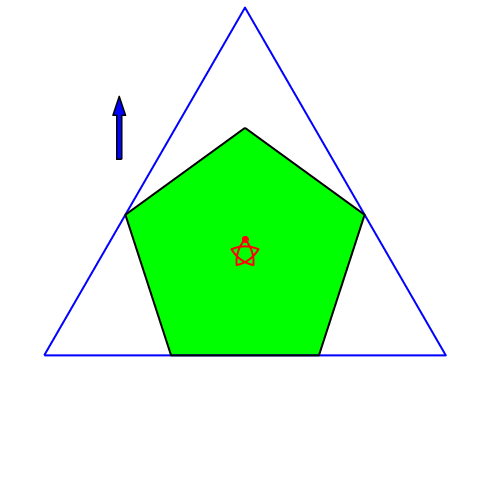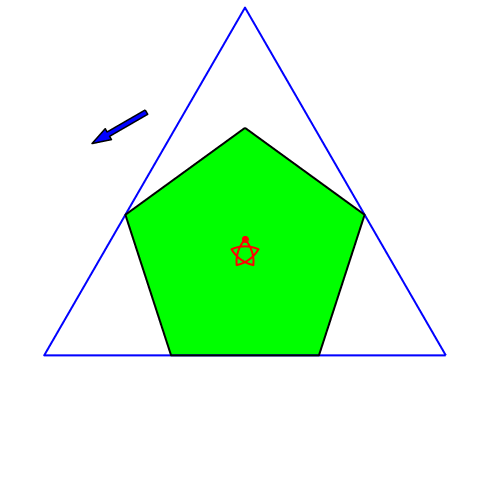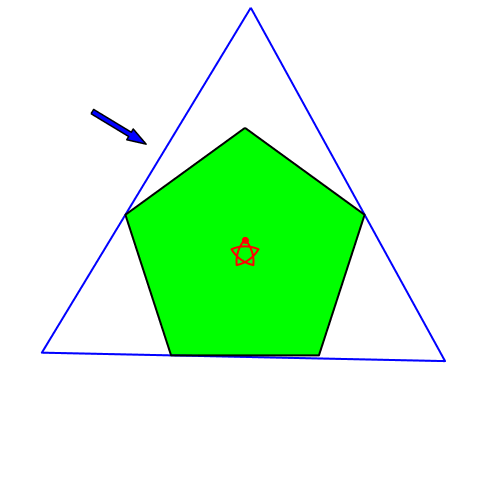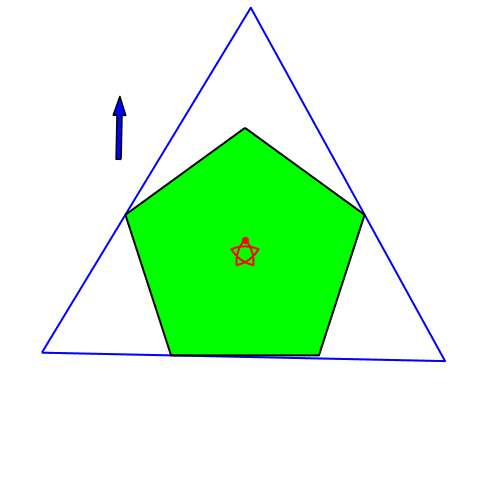
Abb. 7: Regelmäßiges Sechseck

Der rote Punkt ist stabil. Dies gilt für alle regelmäßigen Vielecke, deren Eckenzahl ein Vielfaches von drei ist.

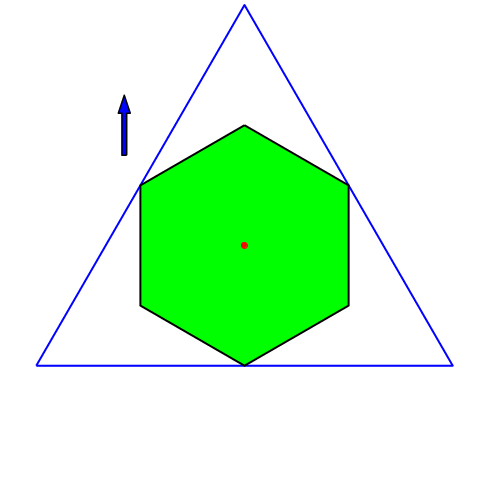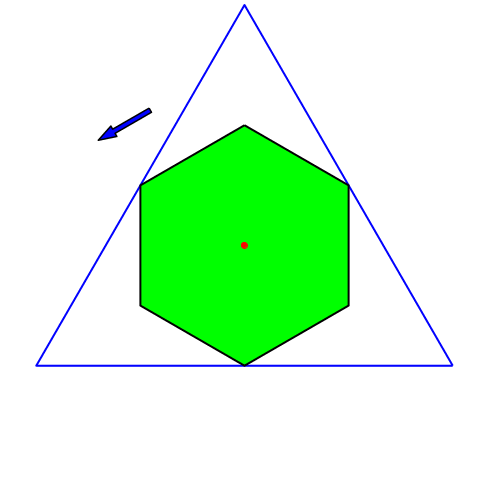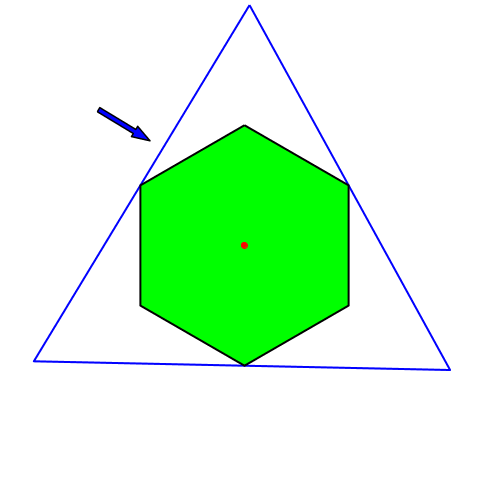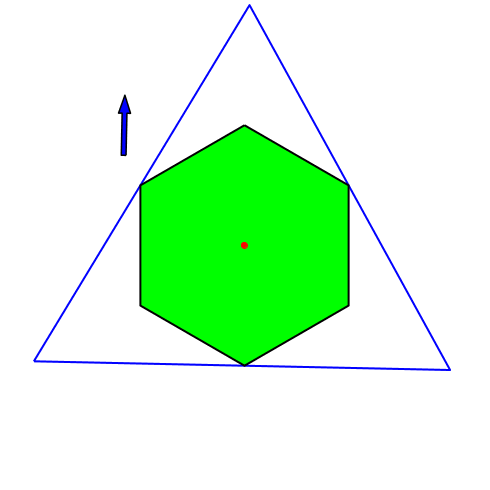
Abb. 8: Regelmäßiges Sechseck

4.5 Regelmäßiges Siebeneck

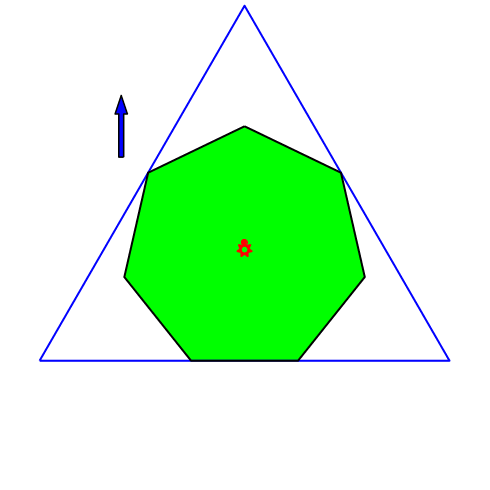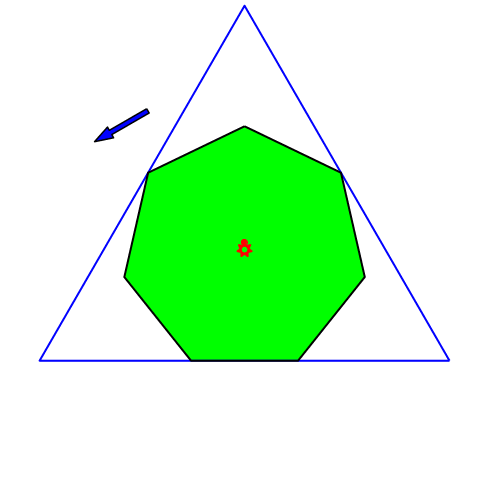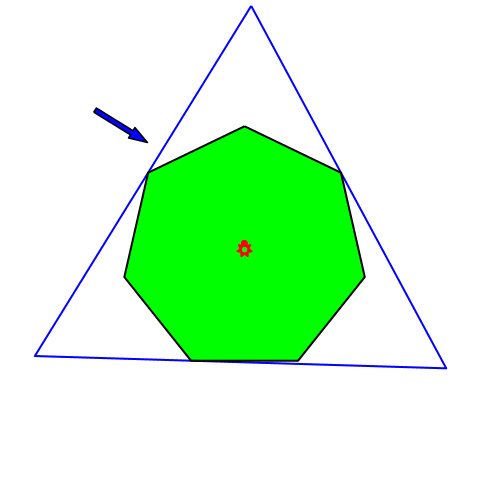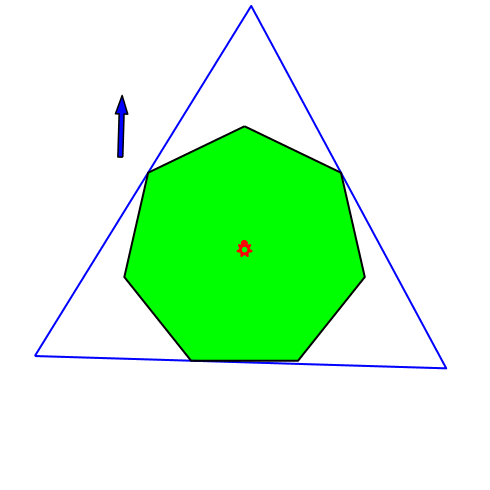
Abb. 9: Regelmäßiges Siebeneck

4.6 Bahnkurven

Die Abbildung 10 zeigt die Bahnkurven für die Eckenzahlen 2, 4, 5, 7, 8, 10, 11, 13. Bei den nach außen gekrümmten Bahnkurven läuft der rote Punkt im positiven Sinn um den Vieleckmittelpunkt, sofern das blaue gleichseitige Dreiecke im positiven Drehsinn dreht. Aus der Sicht des roten Punktes haben wir in jedem Fall eine positive Kurvenkrümmung.

Abb. 10: Bahnkurven

Weblink

Thomas Jahre: Das Zentrum ist nicht die Mitte

https://www.schulmodell.eu/2704-das-zentrum-ist-nicht-die-mitte.html

Hans Walser: Mittelpunkt

http://www.walser-h-m.ch/hans/Miniaturen/M/Mittelpunkt/Mittelpunkt.html