1 Worum es geht

Konstruktion des Mittelpunktes einer Strecke ohne Zirkel.

2 Problemstellung

Gegeben seien eine Strecke und eine dazu parallele Gerade (Abb. 1).

Abb. 1: Strecke und parallele Gerade

Gesucht ist der Mittelpunkt der Strecke, ohne Verwendung eines Zirkels.

3 Vorgehen

Wir wählen einen beliebigen Punkt außerhalb der Streckengeraden und der parallelen Geraden (blau in Abb. 2).

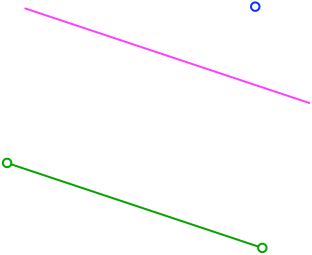
Abb. 2: Wahl eines Punktes

Wir legen die Geraden durch diesen blauen Punkt und die Endpunkte der gegebenen Strecke (blau in Abb. 3). Diese Geraden schneiden wir mit der Parallelen.

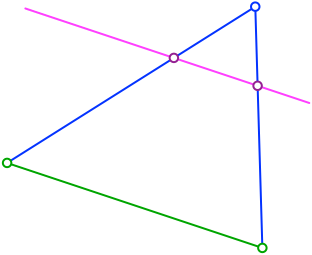
Abb. 3: Geraden

Die Eckpunkte verbinden wir mit den Schnittpunkten der Parallelen und der gegenüberliegenden blauen Geraden (lila in Abb. 4). Wir schneiden die beiden lila Geraden (rot in Abb. 4).

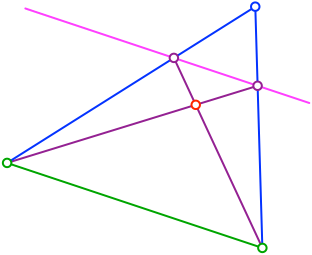
Abb. 4: Verbindungen

Die Gerade durch den blauen und den roten Punkt halbiert die gegebene Strecke (Abb. 5).

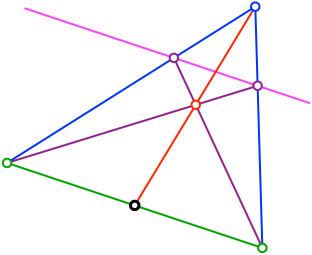
Abb. 5: Mittelpunkt

4 Beweise

4.1 Satz von Ceva

Für den Beweis mit dem Satz von Ceva verwenden wir die Bezeichnungen der Abbildung 6.

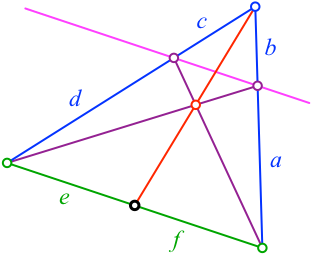
Abb. 6: Beweisfigur

Nach dem Satz von Ceva ist ace / bdf = 1.

Wegen dem Strahlensatz ist a/b = d/c, also ac = bd.

Daraus folgt e/f = 1. Der schwarze Punkt ist also der Mittelpunkt.

4.2 Affine Abbildung

Wir bilden das durch die Endpunkte der gegebenen Strecke und den gewählten blauen Punkt definierte Dreieck affin auf ein gleichschenkliges Dreieck mit der Spitze im blauen Bildpunkt ab. An den Streckenverhältnissen ändert das nichts. Im gleichschenkligen Dreieck folgt die Mittelpunkteigenschaft aus der Symmetrie.

5 Hintergrund

Die Konstruktion einer Parallelen zu einer gegebene Strecke benötigt den Zirkel.