1 Worum geht es?

Versuch, einen geometrischen Sachverhalt im Dreieck ohne Formeln und Winkelberechnungen zu beweisen. Die Abbildungen enthalten keine Beschriftungen. Reine Geometrie.

2 Ausgangslage

In einem Dreieck zeichnen wir den Höhenschnittpunkt und den Mittelpunkt einer Seite (Abb. 1).

Abb. 1: Höhenschnittpunkt und Seitenmitte

Wir verbinden die Seitenmitte mit dem Höhenschnittpunkt und zeichnen dort die Orthogonale dazu. Diese schneiden wir mit den beiden anderen Dreiecksseiten (Abb. 2).

Abb. 2: Orthogonale

3 Behauptung

Die so entstandene Strecke wird durch den Höhenschnittpunkt halbiert.

Dies ist zu beweisen.

4 Schlüsselidee

Wir spiegeln den Höhenschnittpunkt an der Seitenmitte und erhalten so ein Parallelogramm (Abb. 3). Die Seitenmitte halbiert auch die zweite Diagonale des Parallelogramms.

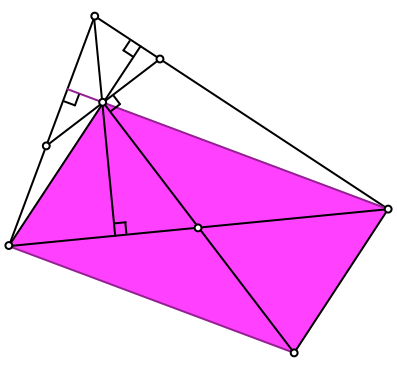
Abb. 3: Parallelogramm

5 Ähnliche Dreiecke

Wir arbeiten nun mit den beiden markierten Dreiecken (Abb. 4).

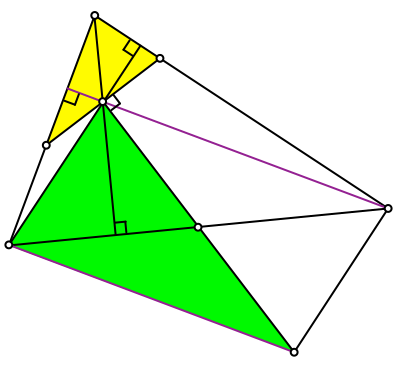
Abb. 4: Zwei Dreiecke

Die Seiten dieser Dreiecke sind paarweise orthogonal (Abb. 5).

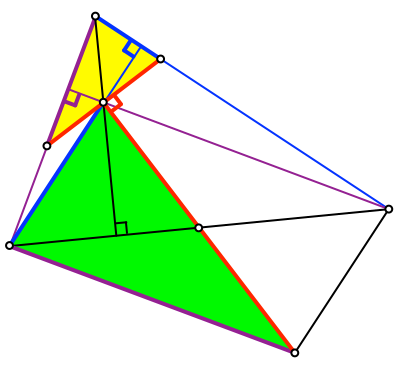
Abb. 5: Orthogonale Seiten

Die beiden Dreiecke sind also gleichsinnig ähnlich und können durch eine Drehstreckung aufeinander abgebildet werden.

6 Drehstreckung

Bei dieser Drehstreckung wird die Seitenmitte des Ausgangsdreieckes auf die Seitenmitte des gelben Dreieckes abgebildet. Somit ist Behauptung bewiesen.

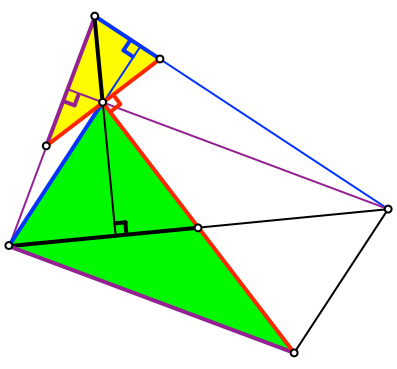
Abb. 6: Abbildung des Mittelpunktes

Literatur

Posamentier, Alfred S. and Geretschläger, Robert: Geometric Gems: An Appreciation for Geometric Curiosities. Volume 1: The Wonders of Triangles. Worlds Scientific. 2024.