Hans Walser, [20080110a]

Möbiusbänder

Anregung: E. A. F., B. und [Kroll 2007]

1 Worum es geht

Das Möbiusband wird so modifiziert, dass es (mit Selbstdurchdringung) in der Einheitskugel liegt.

2 Wendelfläche im Zylinder

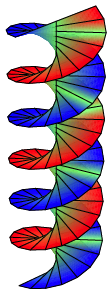
Wendelfläche im Zylinder

Die Wendelfläche hat drei „Doppeltwists“.

3 Zusammenbiegen zum Torus

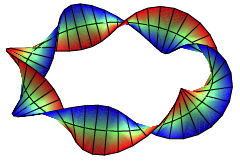
Wir biegen den Zylinder zum Torus

Die „verbogene“ Wendelfläche hat die Parameterdarstellung:

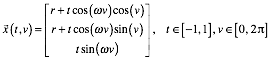
In unserem Beispiel ist ; das ist der Radius des Kreises in der Torusseele. Weiter ist . Dies sehen wir daran, dass wir drei „Doppeltwists“ haben.

Wir variieren nun die Werte und .

4 Variationen von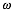

Für ergibt sich ein halber Doppeltwist, also ein einfacher Twist. Das ist das so genannte Möbius-Band.

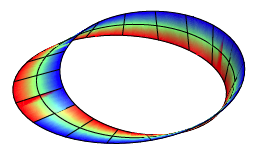
Möbiusband,

Das Möbiusband ist nicht orientierbar, wie aus dem brutalen Farbwechsel links unten ersichtlich ist.

Für erhalten wir eine orientierbare Fläche.

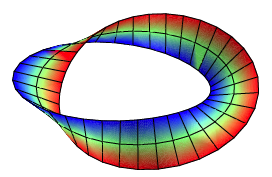
Orientierbare Fläche,

Für ergibt sich wiederum eine nicht orientierbare Fläche, also ein verallgemeinertes Möbiusband.

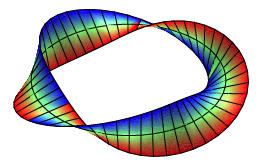
Verallgemeinertes Möbiusband,

Wie ist es bei ?

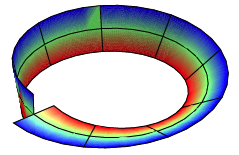
, es geht nicht auf

Nach zwei Umgängen geht es dann auf. Wir erhalten ein Super-Möbiusband mit kreuzförmigem Querschnitt. Es ist nicht orientierbar.

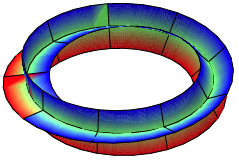
, mit zwei Umgängen

Für braucht es drei Umgänge; die Fläche ist orientierbar. Der Querschnitt der Figur sieht aus wie die drei Mittelpunktsdiagonalen eines regelmäßigen Sechseckes.

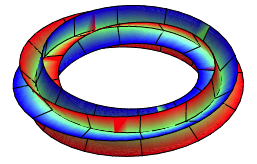
, mit drei Umgängen

Allgemein gilt für eine gekürzte rationale Zahl : nach einem Umgang haben wir vor Ort eine Verdrehung im . Falls q ungerade ist, schließt sich die Fläche nach q Umgängen und ist orientierbar. Falls q gerade ist, schließt sich die Figur nach Umgängen, ist aber nicht orientierbar.

5 In der Kugel

Wir setzen in der Parameterdarstellung ; wir arbeiten also mit:

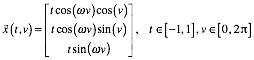
Dann liegt die Fläche in der Einheitskugel.

Für ergibt sich:

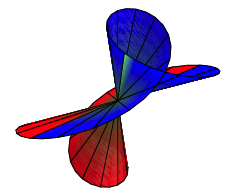
Möbiusband in der Kugel

Das „Band“ ist nicht orientierbar, wie der Färbung glauben dürfen, welche aus der Parametrisierung der Fläche hervorgeht. Wenn wir allerdings das Zentrum entfernen, bleibt eine zusammenhängende orientierbare Fläche übrig. Einen analogen Sachverhalt kennen wir vom gewöhnlichen Möbiusband, wenn wir es längs der Mittellinie entzweischneiden wollen.

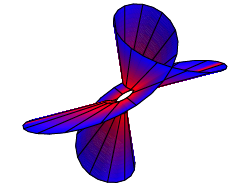
Zentrum entfernt

Für mit zwei Umgängen erhalten wir:

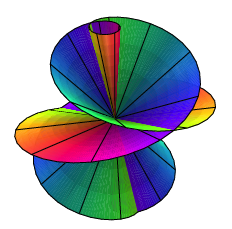
, zwei Umgänge

Für ergibt sich der so genannte vivianische Kegel ([Kroll 2007], S. 16).

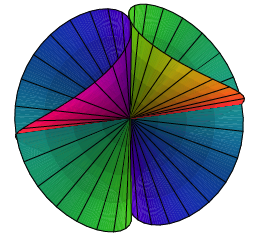
, vivianischer Kegel

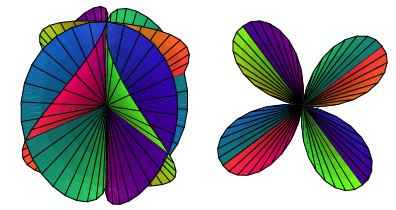
Schließlich noch für und in je zwei Ansichten.

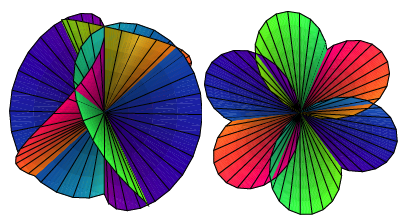
Literatur

[Kroll 2007] Kroll, Wolfgang: Räumliche Kurven und Flächen in phänomenologischer Behandlung. © 2007 by Wolfgang Kroll, Marburg. ISBN 978-3-00-021836-1
http://www.sciface.com/education/data/more/krollkuf/index.html