Hans Walser, [20191027]
Mbiusband
Anregung: Vo§ 2009
1 Worum geht es?
Regelm§ige Vielecke und Mbiusband. Parittsproblem.
2 Zweifarbiger Streifen
Wir kleben zwei verschiedenfarbige Streifen auf Sto§ nebeneinander (Abb. 1). Der Autor hat dazu mit transparentem Klebeband gearbeitet.

Abb. 1: Zweifarbiger Streifen
Wir haben auf der Vorder- und der Rckseite je die beiden Farben rot und grn.
3 Falten auf der Basis des gleichseitigen Dreieckes
Wir falten den Streifen der Abbildung 1 um 60¡ nach oben (Abb. 2.1).

Abb. 2.1: 60¡ nach oben falten
Wir haben jetzt eine doppelte berlagerung in Form eines gleichseitigen Dreieckes.
Anschlie§end falten wir nach unten gem§ Abbildung 2.2. Die neue Faltkante ist bndig zur Oberkante des Streifens. Das Dreieck ist jetzt bereits dreifach berlagert.

Abb. 2.2: Nach unten falten
Schlie§lich falten wir nach rechts gem§ Abbildung 2.3. Das Dreieck ist jetzt vierfach berlagert.

Abb. 2.3: Nach rechts falten
Wir haben nun von au§en gesehen einen Streifen mit einem Farbwechsel. Wenn wir das linke und das rechte Ende identifizieren, das hei§t den Streifen zum Zylinder aufbiegen und die Enden zusammenkleben ergibt sich ein Mbiusband.
4 Falten auf der Basis des regelm§igen Fnfeckes
Die Abbildungsfolge 3.0 bis 3.5 zeigt das entsprechende Vorgehen auf der Basis des regelm§igen Fnfeckes. Das freie Ende ist von Schritt zu Schritt um 144¡ versetzt. Zudem wird bei jedem Schritt die Farbreihenfolge (im positiven Drehsinn) vertauscht.
Es braucht einen ziemlich langen Streifen.
![]()
Abb. 3.0: Ausgangslage

Abb. 3.1
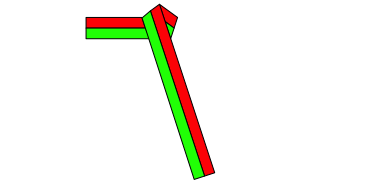
Abb. 3.2
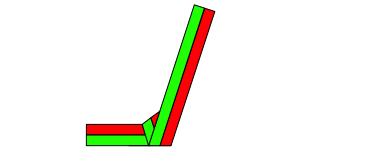
Abb. 3.3
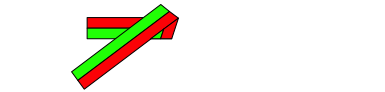
Abb. 3.4
![]()
Abb. 3.5: Streifen mit Farbwechsel
5 Falten auf der Basis des regelm§igen Siebeneckes
Die Abbildungsfolge 4.0 bis 4.7 zeigt eine Mglichkeit auf der Basis des regelm§igen Siebeneckes. Der Streifen ist bereits vorgefaltet. Die Faltlinien sind abwechslungsweise Talfalte und Bergfalte.
![]()
Abb. 4.0: Ausgangslage
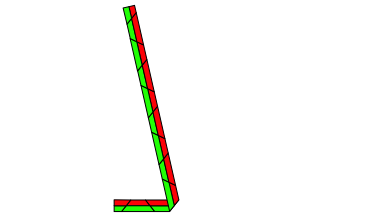
Abb. 4.1: Erster Schritt
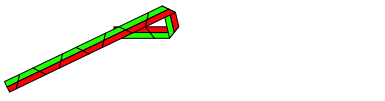
Abb. 4.2
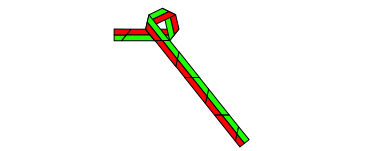
Abb. 4.3
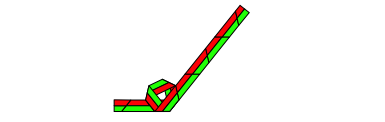
Abb. 4.4
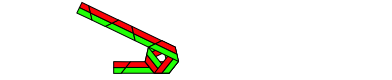
Abb. 4.5

Abb. 4.6
![]()
Abb. 4.7: Endlage
Die Abbildung 5 zeigt die Endlage vergr§ert. Das Loch in der Mitte ist ein regelm§iges Siebeneck, obwohl es nicht so scheint. Wir haben eine optische Tuschung.
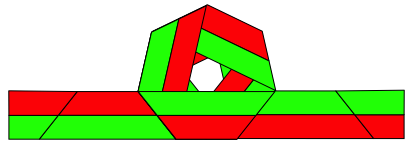
Abb. 5: Endlage
Die Abbildungsfolge 6.0 bis 6.1 zeigt eine zweite Lsung.
![]()
Abb. 6.0: Ausgangslage
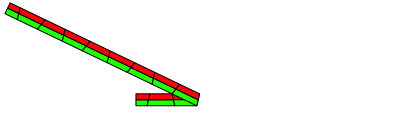
Abb. 6.1: Erster Schritt
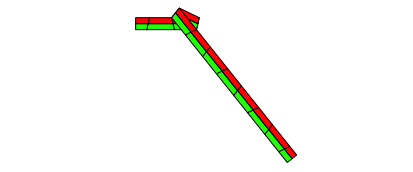
Abb. 6.2
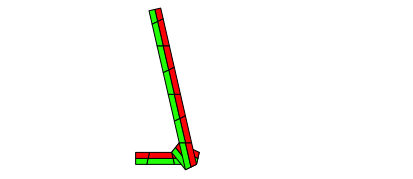
Abb.6.3
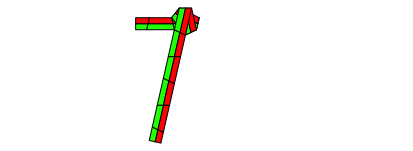
Abb. 6.4
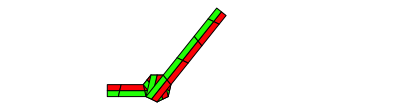
Abb. 6.5

Abb. 6.6
![]()
Abb. 6.7: Endlage
Die Abbildung 7 zeigt die Endlage vergr§ert.
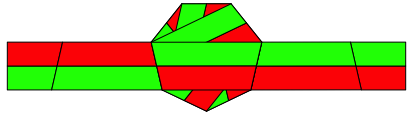
Abb. 7: Endlage
Beim regelm§igen Siebeneck gibt es zwei Diagonalentypen. Kurze Diagonalen, welche eine Ecke berspringen, und lange Diagonalen, welche zwei Ecken berspringen. Die erste Lsung ist an den kurzen Diagonalen orientiert, die zweite Lsung an den langen Diagonalen.
6 Falten auf der Basis des regelm§igen Neunecks
Es gibt drei Lsungen. Die Abbildung 8 zeigt die Endlage fr die erste Lsung. Das Loch in der Mitte ist ein regelm§iges Neuneck, auch wenn es nicht so scheint.
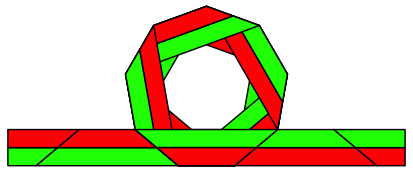
Abb. 8: Erste Lsung
Die Abbildung 9 zeigt die zweite Lsung. Wir sehen, dass 9 durch 3 teilbar ist.
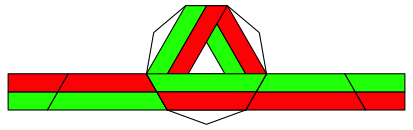
Abb. 9: Zweite Lsung
Die Abbildung 10 zeigt die dritte Lsung.
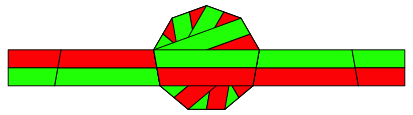
Abb. 10: Dritte Lsung
7 Allgemein
Analog
knnen wir mit einem beliebigen regelm§igen Vieleck ungerader Eckenzahl u verfahren. Fr u > 3 gibt es ![]() Lsungen.
Lsungen.
Literatur
Vo§, Fred (2009): Vom Mbiusband zum V-Band.
Untersuchungen. Entwicklungen. Ergebnisse.
https://fredvoss.files.wordpress.com/2015/05/brosch-29-10.pdf
Weblinks
Vo§, Fred: Vom Mbiusband zum V-Band
https://fredvoss.files.wordpress.com/2015/05/brosch-29-10.pdf
Hans Walser: Mbius-Band flechten
http://www.walser-h-m.ch/hans/Miniaturen/M/Moebius_Band_fl/Moebius_Band_fl.htm
Hans Walser: Mbius-Band
http://www.walser-h-m.ch/hans/Miniaturen/M/Moebiusband/Moebiusband.pdf
Hans Walser: Mbius-Bnder
http://www.walser-h-m.ch/hans/Miniaturen/M/Moebius/Moebius.htm