1 Worum geht es?

Verbiegen der Achse einer Schraubenfläche

2 Schraubenfläche

Die Schraubenfläche der Abbildung 1a ist auf den beiden Seiten verschieden gefärbt. Es hat einen roten und einen blauen Aufgang zu je zwei Runden. In der Abbildung 1b liegt die Achse der Schraubenfläche horizontal.

Abb. 1: Schraubenfläche

3 Geschlossene Achse

Wir biegen die Achse der Schraubenfläche zu einem Kreis (Abb. 2a). Gegebenenfalls werden zusätzliche Runden angefügt (Abb. 2b mit fünf Runden). Erinnert an die Spiralnudeln aus Großmutters Küche.

Abb. 2: Achse zum Kreis gebogen

Wird die Streifenbreite auf den Kreisdurchmesser vergrößert, ergibt sich eine Eigenberührung des Streifens in der Mitte (Abb. 3).

Abb. 3: Blume

4 Halbe Runden

Bei halbzahligen Runden geht es mit den Farben nicht mehr auf (Abb. 4 mit zweieinhalb Runden). In der Abbildung 4b sehen wir deutlich den Farbwechsel.

Abb. 4: Halbzahlige Rundenzahl

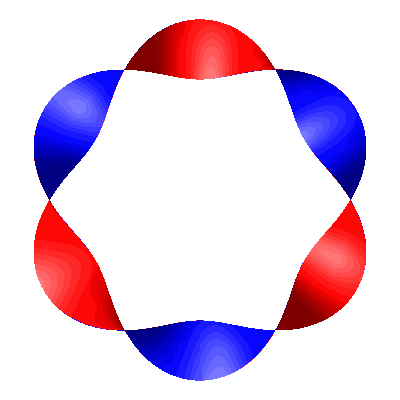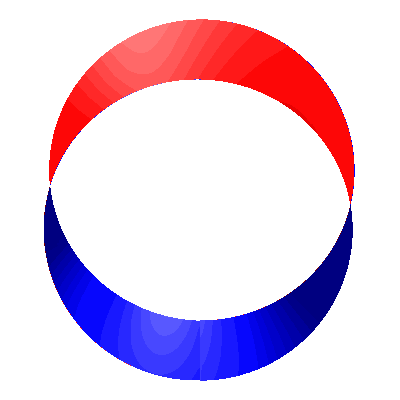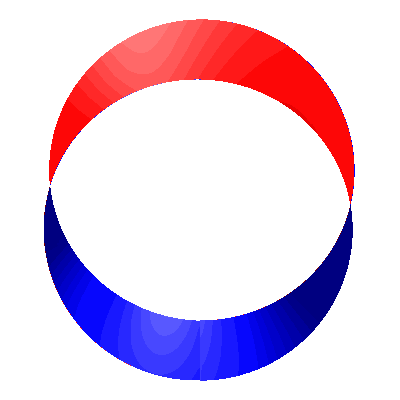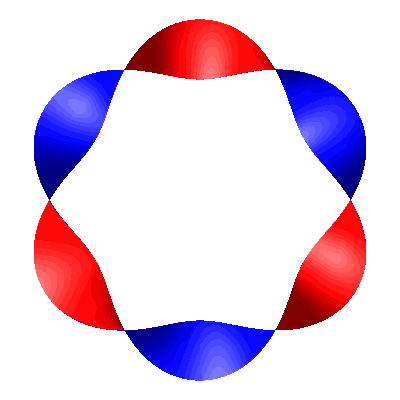
Ein Bild, das Ballon, Flugzeug, Vektorgrafiken enthält.

Automatisch generierte Beschreibung

Abb. 4c: Veränderung der Rundenzahl

Das Band hat sozusagen nur eine Seite. Solche Bänder werden als Möbius-Bänder bezeichnet (August Ferdinand Möbius, 1790-1868). Die Abbildung 5 zeigt das klassische Möbiusband mit nur einer halben Runde.

Abb. 5: Möbiusband

5 Viertel und Drittel

Bei zweieinviertel Runden stehen Anfang und Ende über Kreuz mit einem Drehversatz von 90° (Abb. 6).

Abb. 6: Anfang und Ende stehen über Kreuz

Nach einem weiteren Umlauf geht das Band zwar glatt auf, aber wir haben immer noch das Farbproblem (Abb. 7). Dies liegt daran, dass zwei Mal ein Viertel nur ein Halbes ergibt. Wir haben also immer noch ein Möbiusband. Es hat einen kreuzförmigen Querschnitt.

Abb. 7: Kreuzweises Möbiusband

Bei zweieindrittel Runden haben Anfang und Ende einen Drehversatz von 60° beziehungsweise 120° (Abb. 8).

Abb. 8: Drehversatz 60°

Nach drei Umläufen haben wir ein glattes Band ohne Farbproblem (Abb. 9). Drei Mal ein Drittel gibt eben eins. Der Querschnitt des Bandes ist ein Stern mit sechs Enden.